动态规划---动态规划初步

一：视频讲解（不错）

https://www.bilibili.com/video/BV18x411V7fm（原理）

https://www.bilibili.com/video/BV12W411v7rd/?spm_id_from=333.788.videocard.0（案例）

二：文章讲解

https://www.zhihu.com/question/39948290

 

三：练习

（一）{ 1, 2, 4, 1, 7, 8, 3 }  我们需要进行从中选取不相邻的多个数，使得相加结果最大

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int rec_opt(int arr, int idx);                //开始进行动态规划操作,递归实现
int dp_opt(int arr,int arr_size);        //非递归实现

int main()
{
    int arr[] = { 1, 2, 4, 1, 7, 8, 3 };    //我们需要进行从中选取不相邻的多个数，使得结果最大

    //int res = rec_opt(arr, 6);    
    int res = dp_opt(arr, 7);
    printf("the max component number is %d\n", res);

    system("pause");
    return 0;
}

int dp_opt(int arr[], int arr_size)        //非递归实现
{
    int i,temp_res;
    int *opt = (int*)malloc(sizeof(arr_size)*sizeof(int));    //生成一个和原来数组arr一样大小的数组
    //先正序，生成opt数组数据
    opt[0] = arr[0];
    opt[1] = max(arr[0], arr[1]);    
    
    for (i = 2; i < arr_size; i++)        //先正序计算结果
        opt[i] = max(arr[i] + opt[i - 2], opt[i - 1]);            //对应选和不选两种情况

    return opt[arr_size - 1];            //返回最后一个数字，opt,是最终结果
}


int rec_opt(int arr[], int idx)        //使用递归，效率太低。运算规模达到2^n
{
    int ch_res, unCh_res;

    //先判断结束条件
    if (idx == 0)
        return arr[0];
    else if (idx == 1)
        return max(arr[0], arr[1]);
    //开始进行递归
    else
    {
        ch_res = rec_opt(arr, idx - 2) + arr[idx];            //如果选择了当前的数据（需要加上当前数据），则不能选择相邻的元素
        unCh_res = rec_opt(arr, idx - 1);                        //如果没有选择当前的数据，则可以选择前一个数据
        return max(ch_res, unCh_res);
    }
}

（二）int arr[] = { 3, 34, 4, 12, 5, 2 }, S = 9; //想要从arr中选取若干数字，使得相加结果为S。判断是否存在？

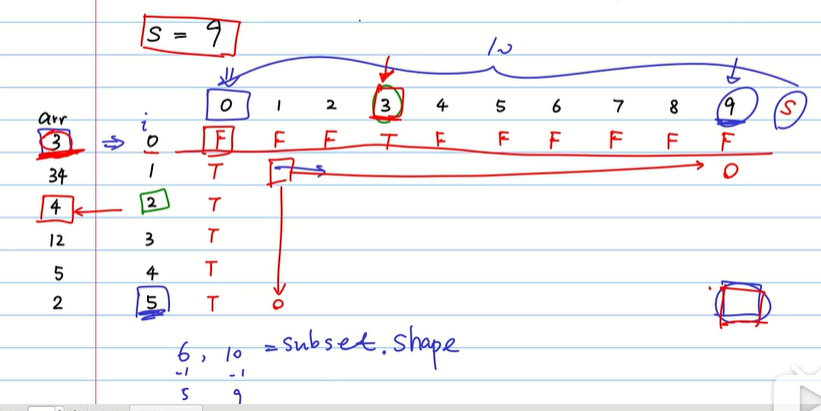
int rec_subset(int arr[], int ind, int s);    //递归实现
int dp_subset(int arr[], int s, int arr_size);    //非递归实现

int main()
{
    int arr[] = { 3, 34, 4, 12, 5, 2 }, S = 9;    //想要从arr中选取若干数字，使得相加结果为S。判断是否存在
    for (; S < 14;S++)
    {
        if (dp_subset(arr, S, 6))
            printf("get a match result for %d\n",S);
        else
            printf("fail to get a match result for %d\n",S);
    }
    system("pause");
    return 0;
}

int rec_subset(int arr[], int ind, int s) //递归实现
{
    if (s == 0)    //先判断退出情况，符合情况，直接返回1
        return 1;
    else if (ind == 0)
        return arr[ind] == s;
    else if (arr[ind] > s)    //如果当前数字大于S，则直接向前执行，跳过这个数字
        return rec_subset(arr, ind - 1, s);    
    else  //正常情况，我们想要判断是否进行选择
        return rec_subset(arr, ind - 1, s - arr[ind]) | rec_subset(arr, ind - 1, s);    //分别对应选和不选，这两种情况。
}

int dp_subset(int arr[], int S,int arr_size)    //非递归实现
{
    //先生成一个二维数组
    int** subset = (int**)malloc(sizeof(int*)*arr_size);
    for (int i = 0; i < arr_size; i++)
        subset[i] = (int*)malloc(sizeof(int)*(S + 1));
    //结合上面 递归，进行初始化操作
    for (int i = 0; i < arr_size; i++)
        subset[i][0] = 1;
    for (int i = 0; i < S + 1; i++)
        if (i == arr[0])
            subset[0][i] = 1;
        else
            subset[0][i] = 0;

    //开始进行动态计算
    for (int i = 1; i < arr_size; i++){
        for (int j = 1; j < S + 1; j++){
            if (arr[i] > j)
                subset[i][j] = subset[i - 1][j];    //对应于当元素大于我们要取得S时，我们直接去查看上一个数据
            else
                subset[i][j] = subset[i - 1][j - arr[i]] | subset[i - 1][j];    //在选和不选中进行判断
        }
    }

    return subset[arr_size - 1][S];
}

（三）机器人寻路问题

 

int dp_path(int arr_m, int arr_n)    //获取mxn网格下左上到右下的走法（只能向下、右移动）的路径数目
{
    int** subPath = (int**)malloc(sizeof(int*)*arr_m);    //初始化二维数组
    for (int i = 0; i < arr_m; i++){
        subPath[i] = (int*)malloc(sizeof(int)*arr_n);
        //memset(subPath[i],0, arr_n*sizeof(int));        //注意memset只能对字节赋初值，对整型无法赋值会变为0x01010101转换为十进制则是16843009    
        for (int j = 0; j < arr_n; j++)                        //对所有网格赋初值为1，到达路径为1（因为第一行和第一列只有一种走法---注意边缘进行初值处理）
            subPath[i][j] = 1;
    }

    for (int i = 1; i < arr_m; i++)    //开始进行动态规划（不要边缘）
        for (int j = 1; j < arr_n; j++)
            subPath[i][j] = subPath[i - 1][j] + subPath[i][j - 1];    //状态方程

    return subPath[arr_m - 1][arr_n - 1];
}

void main()
{
    int pathCount = dp_path(3,7);
    printf("The number of paths taken by the robot in the grid is %d\n", pathCount);　　//28
    system("pause");
}

（四）正则匹配问题

 

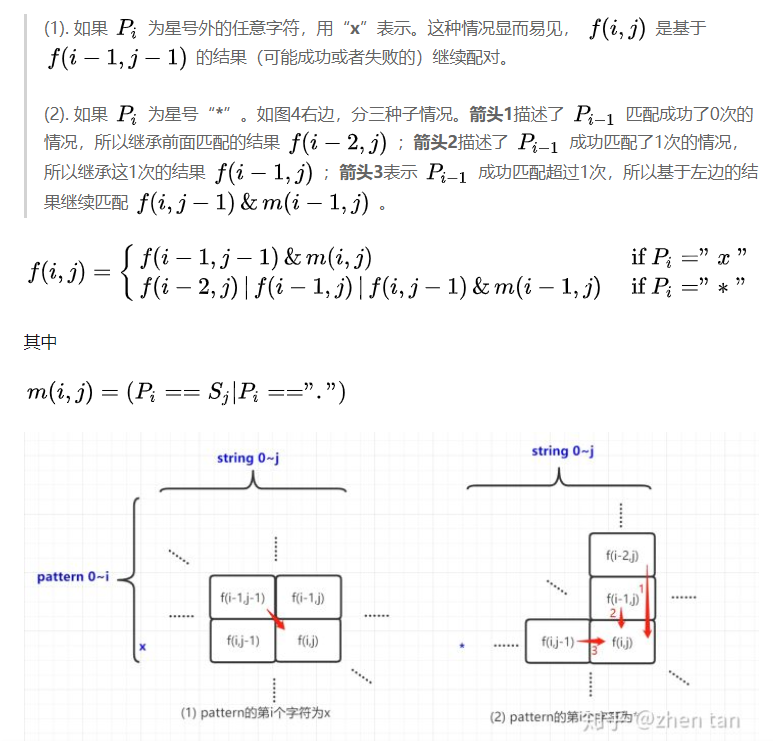
int dp_reg(char* str,char* pat,int str_size,int pat_size)
{
    //注意：由于在状态方程中存在-2，所以我们设置哨兵解决临界问题
    str_size += 1;
    pat_size += 1;
    char *newStr = (char*)malloc(str_size*sizeof(char));
    char *newPat = (char*)malloc(pat_size*sizeof(char));
    sprintf_s(newStr, str_size+1, "_%s", str);
    sprintf_s(newPat, pat_size + 1, "_%s", pat);

    int** subReg = (int**)malloc(sizeof(int*)*pat_size);    //初始化二维数组
    for (int i = 0; i < pat_size; i++){
        subReg[i] = (int*)malloc(sizeof(int)*str_size);
        memset(subReg[i], 0, str_size*sizeof(int));        //注意memset只能对字节赋初值，对整型无法赋值会变为0x01010101转换为十进制则是16843009    
    }
    subReg[0][0] = 1;
    
    //处理异常情况
    if (newPat[1] == '*')
        return 0;
    if (pat_size == str_size && pat_size == 1)
        return 1;
    if (pat_size == 1)
        return 0;

    //开始动态规划
    for (int i = 1; i < pat_size; i++){
        if (newPat[i] == '*')
            subReg[i][0] = subReg[i - 2][0];
        for (int j = 1; j < str_size; j++){
            //状态方程
            int cur_ch;
            if (newPat[i] != '*')
            {
                cur_ch = newPat[i] == newStr[j] | newPat[i] == '.';
                subReg[i][j] = subReg[i - 1][j - 1] & cur_ch;
            }
            else
            {
                cur_ch = newPat[i - 1] == newStr[j] | newPat[i] == '.';    //对于*号，我们要比较前面的字母
                //分为匹配0、1、大于1这几种情况
                //对于0，我们去匹配pat中前一个字母的状态-2
                //对于1，我们匹配pat当前要匹配的字母状态-1
                //对于大于1，我们匹配str前一个字母的状态
                subReg[i][j] = subReg[i - 2][j] | subReg[i - 1][j] | subReg[i][j - 1] & cur_ch;    //注意后面&是对前面所有的操作
            }
        }
    }

    return subReg[pat_size - 1][str_size - 1];
}

void main()
{
    char str[] = "aab";
    char pattern[] = "c*a*b";

    printf("%d\n", dp_reg(str, pattern, strlen(str), strlen(pattern)));
    system("pause");
}