# [洛谷1345] 奶牛的电信 （最大流最小割）

[洛谷1345] 奶牛的电信 （最大流最小割）

洛谷1345

题意

给出点的个数，边的条数，源点和汇点。

分别给出与边相连的点，边权为1。

求最少删去多少点使得源点和汇点不连通。

思路

• 割点转割边+最大流最小割

• 最大流最小割定理：最大流=最小割

• 割：删去一些边使得源点和汇点不连通

题目是求删点，最大流最小割算法删的是边，所以要割点转化为割边（最大流最小割其实并不能算一个算法，只是将求最小割转化为求最大流）

建模

将一个点拆成两个点，其中一个点负责连接入边，另外一个点负责连接出边，拆成的两个点之间边权为1，表示只能一个点只能删一次（如果这条边被删了，入边和出边无法连通表示点被删除）。由于求的是删除点的个数，其他的边置为INF。

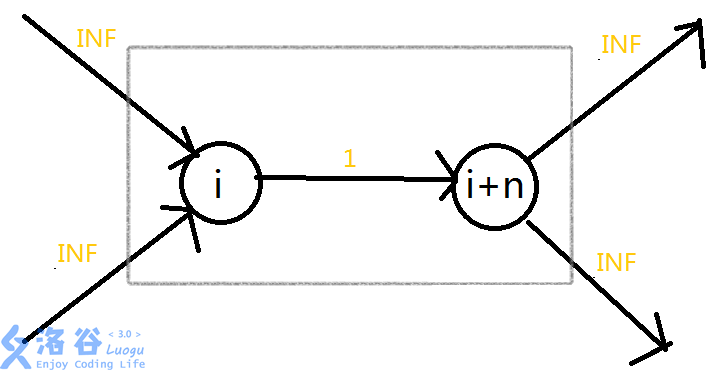
举个栗子

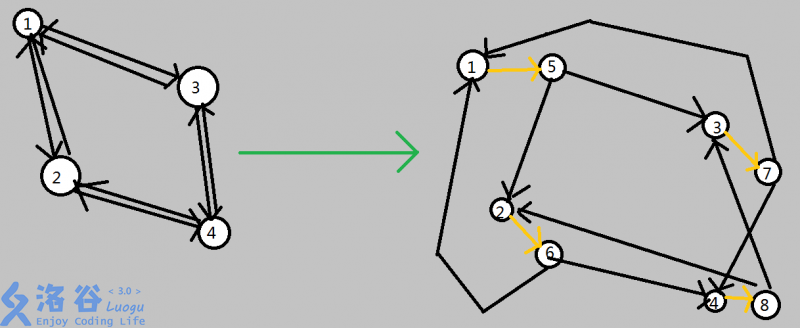
代码实现

这题我的代码建了反向边，但是有些Ac代码没有建反向边，我也不知道为什么可以不用建反向边，望路过的大佬指点指点。

#include <bits/stdc++.h>
using namespace std;
#define fre freopen("data.in","r",stdin);
#define ms(a) memset((a),0,sizeof(a))
#define go(i,a,b) for(register int (i)=(a);(i)<(b);++(i))
#define rep(i,a,b) for(register int (i)=(a);(i)<=(b);++(i))
#define sf(x) scanf("%d",&(x))
#define reg register
typedef long long LL;
const int inf=(100000);
const int maxn=1e2+5;
const int maxm=6e2+5;
struct node{int to,flow,next;}e[(maxn+maxm)<<1];
int n,m,s,t;
int head[maxn<<1],cur[maxn<<1],deep[maxn<<1];
int cnt;
queue<int> q;
inline void add(int x,int y,int w){
    e[cnt].to=y,e[cnt].flow=w,e[cnt].next=head[x];
    head[x]=cnt++;
}

inline bool bfs(){
    memset(deep,0,sizeof(deep));
    deep[s]=1;q.push(s);
    int u,v;
    while(!q.empty()){
        u=q.front();q.pop();
        for(int i=head[u];~i;i=e[i].next){
            v=e[i].to;
            if(!deep[v]&&e[i].flow){
                deep[v]=deep[u]+1;
                q.push(v);
            }
        }
    }
    return deep[t];
}
int dfs(int now,int nowFlow){
    if(now==t)return nowFlow;
    int totFlow=0;
//    if(now==10){
//        puts("bug\n");
//    }
    for(int i=cur[now],v;~i;i=e[i].next){
        cur[now]=i;v=e[i].to;
//        if(v==5){
//            puts("bug\n");
//        }
        if(deep[v]==deep[now]+1&&e[i].flow){
            int canFlow=dfs(v,min(nowFlow,e[i].flow));
            if(!canFlow)continue;
            totFlow+=canFlow,nowFlow-=canFlow;
            e[i].flow-=canFlow;e[i^1].flow+=canFlow;
            if(nowFlow<=0)break;
        }
    }
    if(totFlow<=0)deep[now]=-2;
    return totFlow;
}
inline void Dinic(){
    int maxFlow=0;
    while(bfs()){
      //  puts("bfs");
        memcpy(cur,head, sizeof(head));
        maxFlow+=dfs(s,inf);
      //  puts("dfs");
    }
    printf("%d\n",maxFlow);
}
int main(){
    scanf("%d%d%d%d",&n,&m,&s,&t);
    memset(head,-1,sizeof(head));
    rep(i,1,n){
        add(i,i+n,1);add(i+n,i,0);
    }
    s+=n;
    for(int i=0,x,y;i<m;++i){
        scanf("%d%d",&x,&y);
        add(x+n,y,inf);add(y+n,x,inf);
    }
    Dinic();
    return 0;
}