排序算法之合并排序

合并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

合并排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。合并排序也叫归并排序。 

 

摘自百科

 

 

声明排序方法，

public static void mergeSort(int[] A,int s,int e){}

因为要多次拆分数组为子序列，所以要用到递归拆分，递归首先结束条件。也就是当数组个数为1的时候，代表这个数组是有序的。

public static void mergeSort(int[] A,int s,int e){
        if(e-s<=1){
            //一个或0个则是有序序列
            return ;
        }
    }

然后进行数组拆分，计算数组的中间长度，二分法。

int mid = (e-s)/2;

然后使用自带方法进行拆切

int[] B1 = Arrays.copyOfRange(A,s,mid);
int[] B2 = Arrays.copyOfRange(A,mid,e);

切完后的数组只是对半切开，所以要进行递归拆切直到最后剩下有序的数组。

mergeSort(B1,0,mid);
mergeSort(B2,0,B2.length);

声明方法进行拆切后的数组排序与合并。

public static void doMergeSort(int[] A,int[] s,int[] e){}

声明两个下标，也就是合并数组的index.

int sJ = 0;
int eK = 0;

进行排序合并数组。

for (int i = 0; i < A.length; i++) {
     if(s[sJ]<e[eK]){
                A[i]=s[sJ];
                sJ++;
            }else{
                A[i]=e[eK];
                eK++;
            }
}    

如下图所示的对比后插入数组。

 

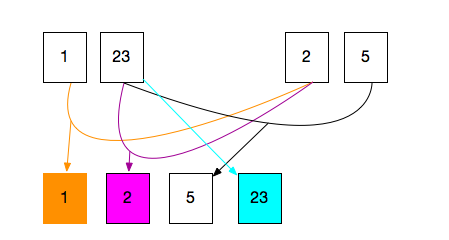
 首先1和2对别，1小，就插入第一个；

第二次23和2对比，2小，就插入第二个。

第三次，23和5对比，5小，就插入第三个。

第四次，23和没有数字对比，则插入最后。

这里需要注意的是，23对比的时候会提示数组越界。因为第二个数组已经用完了，所以无法参与对比。

这时候我们可以在代码中进行判断，如果第二个数组已经不存在数据则第一个数组胜出。第一个数组已经读到最后同样的道理。加个判断如下：

for (int i = 0; i < A.length; i++) {
            if(sJ>=s.length || eK>=e.length){
                if(sJ>=s.length){
                    A[i]=e[eK];
                    eK++;
                }else
                if(eK>=e.length){
                    A[i]=s[sJ];
                    sJ++;
                }
            } else if(s[sJ]<e[eK]){
                A[i]=s[sJ];
                sJ++;
            }else{
                A[i]=e[eK];
                eK++;
            }
        }

可以看到上面的代码很挫，进行代码修改，每个都加个边界值。如下代码所示：

public static void mergeSort(int[] A,int s,int e){
        if(e-s<=1){
            //一个或0个则是有序序列
            return ;
        }
        // 例如  [0-6] [0-3][3-6], [3-4] [4-6]
        // 计算切断中心下标
//        int mid = (e-s)/2+s;
        int mid = (e+s)/2;
        // 开始位置 ,结束位置  前半段
        mergeSort(A,s,mid);
        // 开始位置，结束位置  后半段
        mergeSort(A,mid,e);
        doMergeSort(A,s,e,mid);
    }

public static void doMergeSort(int[] A,int s,int mid,int e){
        // 把数组分为两部分，  s-mid  mid -e   然后进行排序合并
        int[] B1 = Arrays.copyOfRange(A,s,mid+1);
        int[] B2 = Arrays.copyOfRange(A,mid,e+1);
        // 防止越界添加边界值，数组多一位
        B1[B1.length-1]=B2[B2.length-1]=Integer.MAX_VALUE;
        int sJ = 0;
        int eK = 0;
        for (int i = s; i < e; i++) {
            if(B1[sJ]<B2[eK]){
                A[i]=B1[sJ];
                sJ++;
            }else{
                A[i]=B2[eK];
                eK++;
            }
        }
    }

 

 

 

 

 

 

 

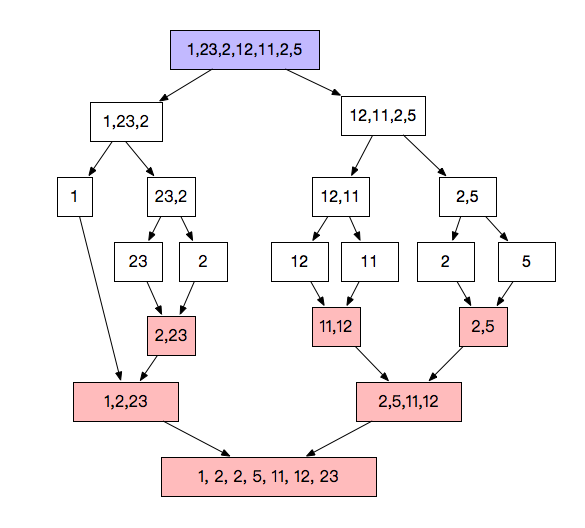
下面提供校验方法：

private static void checkSortArray(int[] array) {
        for (int i = 0; i < array.length-1; i++) {
            if(array[i]>array[i+1]){
                System.err.println("排序错误,排序错误,排序错误,排序错误");
                break;
            }
        }
    }

    private static int[] getReandowArray(int length) {
        int[] array = new int[length];
        for (int j = 0; j < length; j++) {
            array[j]=(int) (Math.random()*length);
        }
        return array;
    }