快速傅里叶变换(FFT)随笔
终于学会了FFT,水一篇随笔记录一下
前置知识网上一大堆,这里就不多赘述了,直接切入正题
01 介绍FFT
这里仅指出FFT在竞赛中的一般应用,即优化多项式乘法
一般情况下,计算两个规模为$n$的多项式相乘的结果,复杂度为$O(n^2)$,但是神奇的FFT可以将其优化至$O(nlogn)$
FFT的过程一般为:
多项式的系数表示$\longrightarrow$多项式的点值表示$\longrightarrow$多项式的系数表示
网上对每一步的叫法都有一定出入,这里称第一步变换为快速傅里叶变换,第二步为快速傅里叶逆变换
02快速傅里叶变换
先指出,接下来的每个$n$都是$2$的整数次幂
首先我们有一个已知系数表达的$n$项的多项式
$A(x)=a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1}$
要确定其的点值表达$(y_0,y_1,y_2,\dots,y_{n-1})$,朴素的做法就是取$n$个不同值代进去,这么做显然是$O(n^2)$
下面介绍快速傅里叶变换的做法
首先将多项式按照奇偶分类
$A(x)=(a_0+a_2x^2+\dots+a_{n-2}x^{n-2})+(a_1x+a_3x^3+\dots+a_{n-1}x^{n-1})$
$A(x)=(a_0+a_2x^2+\dots+a_{n-2}x^{n-2})+x\cdot(a_1+a_3x^2+\dots+a_{n-1}x^{n-2})$
设
$A_1(x)=a_0+a_2x+\dots+a_{n-2}x^{\tfrac{n-2}{2}}$
$A_2(x)=a_1+a_3x+\dots+a_{n-1}x^{\tfrac{n-2}{2}}$
不难发现
$A(x)=A_1(x^2)+xA_2(x^2)$
令$k<\frac{n}{2}$
将$\omega_{n}^k$代入得
$A(\omega_{n}^k)=A_1(\omega_{n}^{2k})+\omega_{n}^{k}A_2(\omega_{n}^{2k})$
$A(\omega_{n}^k)=A_1(\omega_{\tfrac{n}{2}}^{k})+\omega_{n}^{k}A_2(\omega_{\tfrac{n}{2}}^{k})$
将$\omega_{n}^{k+\frac{n}{2}}$代入得
$A(\omega_{n}^{k+\tfrac{n}{2}})=A_1(\omega_{n}^{2k+n})+\omega_{n}^{k+\tfrac{n}{2}}A_2(\omega_{n}^{2k+n})$
$A(\omega_{n}^{k+\tfrac{n}{2}})=A_1(\omega_{n}^{2k}\cdot\omega_{n}^{n})-\omega_{n}^{k}A_2(\omega_{n}^{2k}\cdot\omega_{n}^{n})$
$A(\omega_{n}^{k+\tfrac{n}{2}})=A_1(\omega_{n}^{2k})-\omega_{n}^{k}A_2(\omega_{n}^{2k})$
$A(\omega_{n}^{k+\tfrac{n}{2}})=A_1(\omega_{\tfrac{n}{2}}^{k})-\omega_{n}^{k}A_2(\omega_{\tfrac{n}{2}}^{k})$
显然的,这两个式子只有常数项不同
当$k$取遍$[0,\frac{n}{2}-1]$中所有值时$k+\dfrac{n}{2}$也取遍$[\dfrac{n}{2},n-1]$中所有值
因此,我们只需要在$[0,\dfrac{n}{2}-1]$中枚举$k$,这样就可以算出$A(\omega_{n}^i)\quad(i\in[0,n-1])$的所有值
如果我们已知$A_1(x),A_2(x)$在$\omega_{\tfrac{n}{2}}^0,\omega_{\tfrac{n}{2}}^1,\dots,\omega_{\tfrac{n}{2}}^{\tfrac{n}{2}-1}$的值,通过上面的两个式子就可以在$O(n)$的时间内求出$A(x)$
而求$A_1(x),A_2(x)$正好是求$A(x)$的子问题,并且可以递归求解
03快速傅里叶逆变换
在上面我们将一个多项式的系数表示转换成了点值表示,这里我们要研究将一个多项式的点值表示转换成系数表示
记$(a_0,a_1,\dots,a_{n-1})$是$A(x)$的系数向量,而我们已知$A(x)$的点值表达为$(A(x_0),A(x_1),\dots,A(x_{n-1}))$
设向量$(d_0,d_1,\dots,d_{n-1})$是以$(a_0,a_1,\dots,a_{n-1})$为系数向量时,快速傅里叶变换求得的点值表示
构造一个多项式$F(x)=d_0+d_1x+d_2x^2+\dots+d_{n-1}x^{n-1}$
设$(c_0,c_1,\dots,c_{n-1})$是$F(x)$在$x=\omega_n^{-k}$时的点值表示,即$c_k=F(\omega_n^{-k})$,也就是$c_k=\sum_{i=0}^{n-1}d_i(\omega_n^{-k})^i$
我们知道$d_k=A(\omega_n^k)$,也就是$d_k=\sum_{j=0}^{n-1}a_j(\omega_n^k)^j$
联立上面两个和式得
$c_k=\sum_{i=0}^{n-1} [\sum_{j=0}^{n-1}a_j(\omega_n^i)^j] (\omega_n^{-k})^i$
$\quad \:=\sum_{i=0}^{n-1} \sum_{j=0}^{n-1}a_j(\omega_n^j)^i (\omega_n^{-k})^i$
$\quad \:=\sum_{j=0}^{n-1} a_j \sum_{i=0}^{n-1} (\omega_n^j \omega_n^{-k})^i$
$\quad \:=\sum_{j=0}^{n-1} a_j \sum_{i=0}^{n-1} (\omega_n^{j-k})^i$
我们分情况讨论后面的一个和式$\sum_{i=0}^{n-1} (\omega_n^{j-k})^i$
$j \neq\ k$
那么后面的一个和式就转换为一个等比求和
$\sum_{i=0}^{n-1} (\omega_n^{j-k})^i=\frac{{(\omega_n^{j-k})}^0 [1-(\omega_n^{j-k})^n]}{1-\omega_n^{j-k}}$
$\qquad \qquad \quad \: \: \:=\frac{1-(\omega_n^{j-k})^n}{1-\omega_n^{j-k}}$
$\qquad \qquad \quad \: \: \:=\frac{1-(\omega_n^n)^{j-k}}{1-\omega_n^{j-k}}$
$\qquad \qquad \quad \: \: \:=\frac{1-1^{j-k}}{1-\omega_n^{j-k}}$
$\qquad \qquad \quad \: \: \:=\frac{0}{1-\omega_n^{j-k}}$
$\qquad \qquad \quad \: \: \:=0$
$j = k$
那么$\omega_n^{j-k} = 1$
$\sum_{i=0}^{n-1} (\omega_n^{j-k})^i = n$
由上面两种情况,我们知道当且仅当$j = k$时,整个式子才有值,其余情况都为$0$
所以有
$c_j=a_jn$
$a_j = \frac{c_j}{n}$
到这里,我们就求出了$A(x)$的系数表达
从整个分析过程看,我们是将$A(x)$的点值表示$(A(x_0),A(x_1),\dots,A(x_{n-1}))$当作一个新的多项式$F(x)$的系数表示,再对$F(x)$做快速傅里叶变换得到$(c_0,c_1,\dots,c_{n-1})$,然后再除以$n$就得到$A(x)$的系数表示了。需要指出的是,快速傅里叶变换中$x=\omega_n^k$但是在逆变换中代入的是$\omega_n^{-k}$
04实现
学会了前面的方法,具体实现就不难了
对于求$C(x)=A(x) \cdot B(x)$
将$A(x)$和$B(x)$都转化成点值表达,即$(a_0,a_1,\dots,a_{n-1})$和$(b_0,b_1,\dots,b_{n-1})$
对应相乘$(a_0b_0,a_1b_1,\dots,a_{n-1}b_{n-1})$,再将这一结果变换成$C(x)$的系数表达就完成了
贴一份C++的代码,这是洛谷上的FFT板子题P3803
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #define MAXN 4000006 using namespace std; class complex { public: complex(){} complex(double a,double b) { this->a=a; this->b=b; } double a,b; }a[MAXN],b[MAXN]; complex operator+ (complex x,complex y) { return complex(x.a+y.a,x.b+y.b); } complex operator- (complex x,complex y) { return complex(x.a-y.a,x.b-y.b); } complex operator* (complex x,complex y) { return complex(x.a*y.a-x.b*y.b,x.a*y.b+x.b*y.a); } const double pi=acos(-1.0); void FFT(int l,complex *arr,int f) { if(l==1) return; int dl=l>>1; complex a1[dl],a2[dl]; for(int i=0;i<l;i+=2) { a1[i>>1]=arr[i]; a2[i>>1]=arr[i+1]; } FFT(dl,a1,f); FFT(dl,a2,f); complex wn=complex(cos(2.0*pi/l),sin(2.0*pi/l)*f),w=complex(1.0,0.0); for(int i=0;i<dl;i++,w=w*wn) { arr[i]=a1[i]+w*a2[i]; arr[i+dl]=a1[i]-w*a2[i]; } } int n,m,N; int main() { scanf("%d%d",&n,&m); for(int i=0;i<=n;i++) scanf("%lf",&a[i].a); for(int i=0;i<=m;i++) scanf("%lf",&b[i].a); N=1; while(N<n+m+1) N<<=1; FFT(N,a,1); FFT(N,b,1); for(int i=0;i<N;i++) a[i]=a[i]*b[i]; FFT(N,a,-1); for(int i=0;i<n+m+1;i++) printf("%d ",(int)(a[i].a/N+0.5)); puts(""); return 0; }
闲着没事干,再贴一份Python的
import numpy as np pi = np.arccos(-1.0) def read(): def get_numbers(): try: read.s = input().split() read.s_len = len(read.s) if read.s_len == 0: get_numbers() read.cnt = 0 return 1 except: return 0 if not hasattr(read, 'cnt'): if not get_numbers(): return 0 if read.cnt == read.s_len: if not get_numbers(): return 0 read.cnt += 1 return eval(read.s[read.cnt - 1]) n = int(read()) m = int(read()) class Complex: # 复数类 def __init__(self, a=0.0, b=0.0): self.a = a self.b = b def __add__(self, other): return Complex(self.a + other.a, self.b + other.b) def __sub__(self, other): return Complex(self.a - other.a, self.b - other.b) def __mul__(self, other): return Complex(self.a * other.a - self.b * other.b, self.a * other.b + self.b * other.a) def fft(num, f, args): if num == 1: return div_num = num >> 1 a1 = [] a2 = [] for i in range(0, num, 2): a1.append(args[i]) a2.append(args[i + 1]) fft(div_num, f, a1) fft(div_num, f, a2) wn = Complex(np.cos(2.0 * pi / num), np.sin(2.0 * pi / num) * f) w = Complex(1.0, 0.0) for i in range(0, div_num): args[i] = a1[i] + w * a2[i] args[i + div_num] = a1[i] - w * a2[i] w = w * wn aa = [] bb = [] for j in range(0, n + 1): aa.append(Complex(float(read()), 0.0)) for j in range(0, m + 1): bb.append(Complex(float(read()), 0.0)) nn = 1 while nn < n + m + 1: nn <<= 1 for j in range(n + 1, nn): aa.append(Complex(0.0, 0.0)) for j in range(m + 1, nn): bb.append(Complex(0.0, 0.0)) fft(nn, 1, aa) fft(nn, 1, bb) for j in range(0, nn): aa[j] = aa[j] * bb[j] fft(nn, -1, aa) for j in range(0, n + m + 1): print(int(aa[j].a / nn + 0.5), end=' ')
无奈Python实在是太慢了……
05结语
总算是学会了快速傅里叶变换,某种程度上说是弥补了过去的某些遗憾吧。
这里贴一张大佬的图,解释了FFT的思路
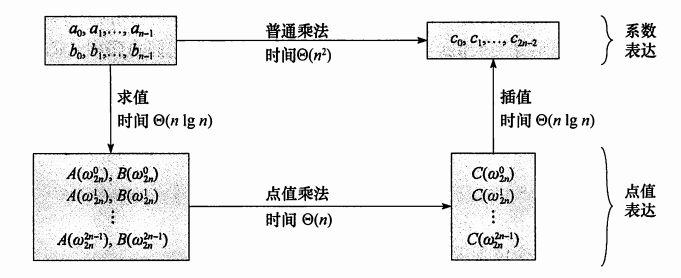
这里也推荐一下大佬的博客,以供参考
快速傅里叶变换(FFT)详解 - 自为风月马前卒 - 博客园 (cnblogs.com)
一小时学会快速傅里叶变换(Fast Fourier Transform) - 知乎 (zhihu.com)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号