【DP】送你一颗圣诞树

Description

再过三个多月就是圣诞节了，小R 想送小Y 一棵圣诞树作为节日礼物。因为他想让这棵圣诞树越大越好，所以当然是买不到能够让他满意的树的，因此他打算自己把这棵树拼出来。
现在，小R 开始画这棵树的设计图纸了。因为这棵树实在太大，所以他采用了一种比较方便的方法。首先他定义了m+ 1 棵树T0 到Tm。最开始他只画好了T0 的图纸：就只有一个点，编号为0。
接着，对于每一棵树Ti，他在第\(T_{ai}\) 棵树的第ci 个点和第\(T_{bi}\) 棵树的第di 个点之间连上了一条长度为li 的边。在Ti 中，他保持\(T_{ai}\) 中的所有节点编号不变，然后如果\(T_{ai}\) 中有s 个节点，他会把\(T_{bi}\) 中的所有节点的编号加上s。
终于，他画好了所有的树。现在他定义一颗大小为n 的树的美观度为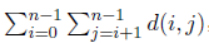
,其中d(i,j)为这棵树中i 到j 的最短距离。
为了方便小R 选择等究竟拼哪一棵树，你可以分别告诉他T1 到Tm 的美观度吗？答案可能很大，请对\(10^9\) + 7 取模后输出。

Input

第一行输入一个正整数T 表示数据组数。每组数据的第一行是一个整数m，接下来m 行每行五个整数ai, bi, ci, di, li，保证0 <= ai, bi < i， 0<= li<= 10^9，ci, di 存在。

Output

对于每组询问输出m 行。第i 行输出Ti 的权值

Sample Input

  1
  2
  0 0 0 0 2
  1 1 0 0 4

Sample Output

  2
  28

Hint

  对于30% 的数据，m <= 8
  对于60% 的数据，m <= 16
  对于100% 的数据，1 <= m<= 60，T<= 100

Solution

啊这道题题解好多
题目大意就是每次询问要将两棵树合并出一颗新树，然后问合并后这棵树上所有点之间的最短路之和
那么我们设\(size[x]\)表示第\(x\)棵树的大小，这个很容易求，设\(size[0]\)为1，然后每次加一下就好了
设\(top[k][x]\)为第k棵树中所有点到x点的路径和
计算就是\(Ans[i] = Ans[a[i]] + Ans[b[i]] + size[a[i]] * size[b[i]] * l[i] + (top[a[i]][c[i]] * size[b[i]]) + (top[a[i]][c[i]] * size[a[i]])\)
（其实就是原本的答案加上新连的这条边带来的贡献）
然后就要来讨论怎么求\(top\)了
我们设\(dis[k][x][y]\)为在第k棵树中，x到y的最短路
那么要分两种情况
1.x在树\(a[k]\)中， 那么\(top[k][x] = top[a[k]][x] + top[b[k]][d[k]] + (l[k] + dis[b[k]][d[k]][x]) * size[b[k]]\)
2.x在树\(b[k]\)中，其实和在左边也差不多，就是x记得减一下\(size[a[k]]\)
然后很恶心的，我们也要来求\(dis\)
若两个点都在不同树上，那\(dis[k][x][y]\)就可以拆成是\(a[k]\)中的\(c[k]\)到\(x\)的最短路径 + \(b[k]\)中的\(d[k]\)到\(y\)的最短路径
那就能得出
\(dis[k][x][y] = dis[a[k]][c[k]][x] + dis[b[k]][d[k]][y]\)
还有\(x\)在树\(b[k]\)中和\(y\)在树\(a[k]\)中的情况，这个很容易推出来，这里就不打了，实在不会可以看代码
哦对，记得mod多一点，还有很玄学的我用\(ll\)代替\(long\ long\)会\(WA\)
但是用了\(int\)代替\(long\ long\)就A了？？？？？？？？（看大佬博客都是这么打的）
然后还要用很玄学的\(pair\)和\(map\)，要不然会炸
这道题直接改到裂开，做的时候对细节多加注意
看在蒟蒻打了这么多题解的份上给个点赞呗?

Code

#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
#define N 65
#define mo 1000000007
#define int long long
using namespace std;

map <pair <int, int>, int> dis[N];
map <int, int> top[N];
int T, m, a[N], b[N], c[N], d[N], l[N], ans[N], size[N];

int disx(int k, int x, int y)
{
	if (x == y || k == 0) return 0;
	if (x > y) swap (x, y);
	pair<int, int>p = make_pair (x, y);
	if (dis[k][p] != 0) return dis[k][p];
	if (y < size[a[k]]) return disx(a[k], x, y);
	else if (x >= size[a[k]]) return disx(b[k], x - size[a[k]], y - size[a[k]]);
	else//x,y不同树
	{
		dis[k][p] = (disx(a[k], x, c[k]) + l[k]) % mo;
		dis[k][p] = (dis[k][p] + disx (b[k], y - size[a[k]], d[k])) % mo;
	}
	return dis[k][p];
}
int topx (int k, int x)
{
	if (k == 0) return 0;
	if (top[k][x] != 0) return top[k][x];
	if (x < size[a[k]])
	{
		top[k][x] = (topx(a[k], x) + topx(b[k], d[k])) % mo;
		top[k][x] = (top[k][x] + (l[k] + disx(a[k], c[k], x)) % mo * (size[b[k]] % mo) % mo) % mo;
	}
	else
	{
		top[k][x] = (topx (b[k], x - size[a[k]]) + topx (a[k], c[k])) % mo;//记得x-size[a[k]]
	    top[k][x] = (top[k][x] + (l[k] + disx (b[k], d[k], x - size[a[k]])) % mo * (size[a[k]] % mo) % mo) % mo;
	}
	return top[k][x];
}
void work ()
{
	scanf ("%intd", &m);
	size[0] = 1;
	for (int i = 1; i <= m; i++)
	{
		scanf ("%lld%lld%lld%lld%lld", &a[i], &b[i], &c[i], &d[i], &l[i]);
		dis[i].clear();
		top[i].clear();
		size[i] = size[a[i]] + size[b[i]]; 
		ans[i] = (ans[a[i]] + ans[b[i]]) % mo;
		ans[i] = (ans[i] + (size[a[i]] % mo) * (size[b[i]] % mo) % mo * l[i] % mo) % mo;
		ans[i] = (ans[i] + topx (a[i], c[i]) * (size[b[i]] % mo) % mo) % mo;
		ans[i] = (ans[i] + topx (b[i], d[i]) * (size[a[i]] % mo) % mo) % mo;
		printf("%lld\n", ans[i]);
	}
}

signed main()
{
	scanf ("%lld", &T);
	for (int i = 1; i <= T; i++)
	  work();
	return 0;
}