2025/5/4测试
AT_abc172_d [ABC172D] Sum of Divisors
题目描述
题意翻译
- \(f(x)\) 表示正整数 \(x\) 的因数个数
- 现在给你一个正整数 $ N $ ,让你求出 $ \sum_{K=1}^N\ K\times\ f(K) $ 。
输入格式
无
输出格式
- 共一行,输出 $ \sum_{K=1}^N\ K\times\ f(K) $ 的结果
- 最后别忘了输出回车
输入输出样例 #1
输入 #1
4
输出 #1
23
输入输出样例 #2
输入 #2
100
输出 #2
26879
输入输出样例 #3
输入 #3
10000000
输出 #3
838627288460105
说明/提示
- $ 1\ \leq\ N\ \leq\ 10^7 $
- $f(1)=1 $ , $ f(2)=2 $ , $ f(3)=2 $ , $ f(4)=3 $ , 所以答案为 $ 1\times\ 1\ +\ 2\times\ 2\ +\ 3\times\ 2\ +\ 4\times\ 3\ =23 $ 。
Translated by qinmingze
思路+AC代码
此题我知道的共有四种算法(如果打表也是一种算法)
算法1:我们看到约数个数很容易想到线性筛求约数个数,时间还是比较可观的(但前提是你得记住板子,好吧其实我没记住),我认为代码无须多言了。
AC code
#include<bits/stdc++.h>
using namespace std;
#define re register
#define int long long
#define endl '\n'
#define lid (id<<1)
#define rid (id<<1|1)
const int N=1e7+10;
inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch-'0');ch=getchar();}return x*f;}inline void write(int x){if(x<0)x*=-1,putchar('-');if(x>9)write(x/10);putchar(x%10+'0');return;}inline int max(int x,int y){return (x<y)?y:x;}inline int min(int x,int y){return (x<y)?x:y;}
int n,d[N],prime[N],vis[N],num[N],ans,cnt;
void get(int n)
{
d[1]=1;
for(int i=2;i<=n;i++)
{
if(!vis[i])
{
prime[++cnt]=i;
d[i]=2;
num[i]=1;
}
for(int j=1;i*prime[j]<=n;j++)
{
int m=i*prime[j];
vis[m]=1;
if(i%prime[j]==0)
{
d[m]=d[i]/(num[i]+1)*(num[i]+2);
num[m]=num[i]+1;
break;
}
else
{
d[m]=d[i]*2;
num[m]=1;
}
}
}
}
signed main()
{
n=read();
get(n);
for(int i=1;i<=n;i++) ans+=i*d[i];
write(ans) ;
return 0;
}
算法2:如果你忘了线性筛求约数个数想硬求是绝对会超时的,不过我们可以采用逆向思维,考虑每个数对它的倍数的贡献。即枚举1~n,令i的小于等于n的倍数的因子数+1.但是这种算法的时间复杂度显然高于线性筛.
AC code
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n;
int factor[10000005];
int res;
signed main()
{
freopen("sum.in","r",stdin);
freopen("sum.out","w",stdout);
cin >> n;
for (int i = 1; i <= n; i ++ )
{
for (int j = i; j <= n; j += i )
{
factor[j] ++ ;
}
}
for (int i = 1; i <= n; i ++ )
res += factor[i] * i;
cout << res;
return 0;
}
算法3:接着考虑一个数对它的倍数的贡献.设一个数为x,则x的贡献为x+2x+3x+4x...(这里指k*f(k)而不单指f(k)),我们发现这不就是一个等差数列吗?且公差为x,首项为x,项数为\(\lfloor \tfrac nx \rfloor\),末项为\(\lfloor \tfrac nx \rfloor\)×\(x\).根据等差数列求和公式即可算得.时间复杂度为\(O\)(\(n\)),十分优秀!(马亮也是十分短小精悍)
AC code
#include<bits/stdc++.h>
using namespace std;
#define re register
#define int long long
#define endl '\n'
#define lid (id<<1)
#define rid (id<<1|1)
inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch-'0');ch=getchar();}return x*f;}inline void write(int x){if(x<0)x*=-1,putchar('-');if(x>9)write(x/10);putchar(x%10+'0');return;}inline int max(int x,int y){return (x<y)?y:x;}inline int min(int x,int y){return (x<y)?x:y;}
int ans,n;
signed main()
{
freopen("sum.in","r",stdin);
freopen("sum.out","w",stdout);
n=read();
for(int i=1;i<=n;i++)
ans+=(i+n/i*i)*(n/i)/2;
cout<<ans;
return 0;
}
算法4:分块打表(我不会)
- T2 匹配

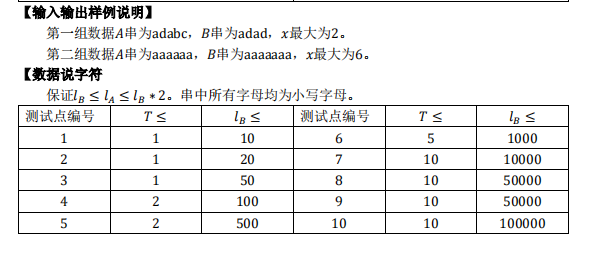
思路+AC代码
本题一眼hashing+二分,挂了...
实际上它并不能用二分,因为二分要满足单调性,但本题并不是说长度长的符合条件短的一定符合条件,因此不能用二分.
正解:其实就是纯hashing,不要忘了unsigned long long.
AC code
#include<bits/stdc++.h>
using namespace std;
#define re register
#define int long long
#define ull unsigned long long
#define endl '\n'
#define lid (id<<1)
#define rid (id<<1|1)
const int N=4e5+10;
const ull P=131;
//inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch-'0');ch=getchar();}return x*f;}inline void write(int x){if(x<0)x*=-1,putchar('-');if(x>9)write(x/10);putchar(x%10+'0');return;}inline int max(int x,int y){return (x<y)?y:x;}inline int min(int x,int y){return (x<y)?x:y;}
ull ha[N],hb[N],p[N];
int ans,la,lb,t;
string a,b;
char c;
ull get(ull h[],int l,int r)
{
return h[r]-h[l]*p[r-l];
}
bool check(int x)
{
if(get(ha,0,x)==get(hb,lb-x,lb)) return true;
return false;
}
signed main()
{
freopen("string.in","r",stdin);
freopen("string.out","w",stdout);
scanf("%lld",&t);
p[0]=1;
for(int i=1;i<=N;i++)p[i]=p[i-1]*P;
while(t--)
{
memset(ha,0,sizeof(ha));
memset(hb,0,sizeof(hb));
cin>>la>>lb;
cin>>a;cin>>c;
b=a.substr(0,lb)+c;
lb++;
for(int i=1;i<=la;i++) ha[i]=ha[i-1]*P+a[i-1];
for(int i=1;i<=lb;i++) hb[i]=hb[i-1]*P+b[i-1];
ans=0;
for(int k=1;k<=la&&k<=lb;k++)
{
if(check(k)) ans=max(ans,k);
}
cout<<ans;puts("");
}
return 0;
}
- T3 回家(
的诱惑)

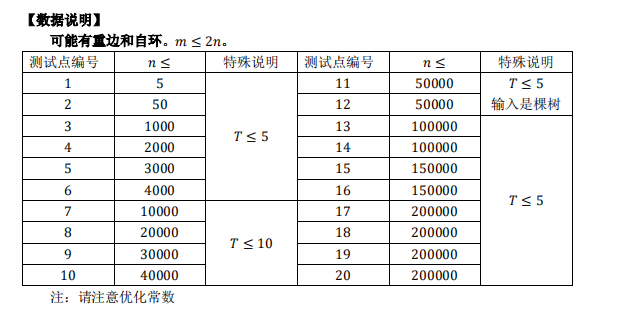

思路+暴力部分分+AC代码
算法1:暴力搜索,dfs删点,30pts
TLE code
#include<bits/stdc++.h>
using namespace std;
#define re register
#define int long long
#define endl '\n'
#define lid (id<<1)
#define rid (id<<1|1)
const int N=4e5+10;
inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch-'0');ch=getchar();}return x*f;}inline void write(int x){if(x<0)x*=-1,putchar('-');if(x>9)write(x/10);putchar(x%10+'0');return;}inline int max(int x,int y){return (x<y)?y:x;}inline int min(int x,int y){return (x<y)?x:y;}
int t,n,m,vis[N],ans;
vector<int> e[N];
priority_queue <int,vector<int>,greater< int> > q;
bool dfs(int s,int t,int cut)
{
if(s==t)return 1;
vis[s]=1;
for(int v:e[s])
{
if(vis[v])continue;
if(v==cut)continue;
if(dfs(v,t,cut))return 1;
}
return 0;
}
signed main()
{
freopen("home.in","r",stdin);
freopen("home.out","w",stdout);
t=read();
while(t--)
{
memset(e,0,sizeof(e));
ans=0;
n=read();m=read();
for(int i=1;i<=m;i++)
{
int u=read(),v=read();
if(u!=v) e[u].push_back(v),e[v].push_back(u);
}
for(int i=2;i<n;i++)
{
memset(vis,0,sizeof(vis));
if(!dfs(1,n,i))
ans++,q.push(i);
}
write(ans);puts("");
while(!q.empty())
{
int x=q.top();
write(x);cout<<" ";
q.pop();
}
puts("");
}
return 0;
}
正解:其实不难想到割点,但问题是并不是每个割点都是必经之路,例如:
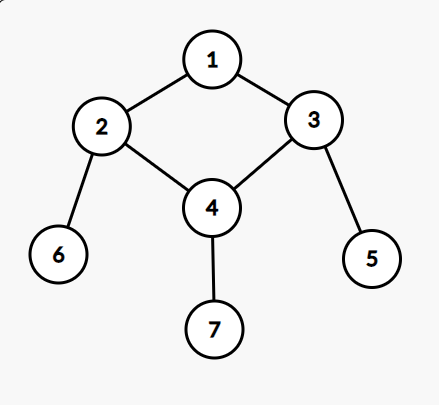
这里2和3都属于割点,但都不是必经之路.因为一个割点不一定把1号点和n号点分到两个不同的块去.不过可以肯定的是必经之路肯定是割点.
其实只要略微改动一下tarjan的模板,用追溯值反应区域,因为dfn[1]=1,显然<=low[x],那么只要low[n]<=dfnx即可保证该割点分1和n到两个不同块中.
AC code
#include<bits/stdc++.h>
using namespace std;
#define re register
#define int long long
#define endl '\n'
#define lid (id<<1)
#define rid (id<<1|1)
const int N=4e5+10;
inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch-'0');ch=getchar();}return x*f;}inline void write(int x){if(x<0)x*=-1,putchar('-');if(x>9)write(x/10);putchar(x%10+'0');return;}inline int max(int x,int y){return (x<y)?y:x;}inline int min(int x,int y){return (x<y)?x:y;}
vector<int> e[N];
int dfn[N],low[N],cut[N],cnt,num,crab[N],cr[N],root;
int n,m,t;
void tarjan(int x)
{
dfn[x]=low[x]=++num;
int flag=0;
for(int y:e[x])
{
if(!dfn[y])
{
tarjan(y);
low[x]=min(low[x],low[y]);
if(dfn[x]<=low[y])
{
flag++;
if(x!=root||flag>1)
if(!cut[x]&&dfn[x]<=low[n]&&x!=1&&x!=n)//注意这里的改动
cut[x]=true,cnt++;
}
}
else
low[x]=min(low[x],dfn[y]);
}
}
signed main()
{
freopen("home.in","r",stdin);
freopen("home.out","w",stdout);
t=read();
while(t--)
{
memset(e,0,sizeof(e));
memset(low,0,sizeof(low));
memset(dfn,0,sizeof(dfn));
memset(cut,0,sizeof(cut));
cnt=0,num=0;
n=read();m=read();
for(int i=1;i<=m;i++)
{
int u=read(),v=read();
if(u!=v) e[u].push_back(v),e[v].push_back(u);
}
for(int i=1; i<=n; i++)
if(!dfn[i])
{
root = i;
tarjan(i);
}
write(cnt);puts("");
for(int i=2;i<n;i++)
if(cut[i])
cout<<i<<" ";
if(cnt)cout<<endl;
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号