傅里叶变换入门

向量的延伸——数组

假设一个k维的向量\(\mathbf{u}\)，我们希望计算这个k维的向量在某个基向量\(\mathbf{v_i}\)上的投影：

\[u_{(v_{i})}=u_{1}v_{i,1}+u_{2}v_{i,2}+\cdots+u_{k}v_{i, k}=\sum_{n=1}^{k}u_{n}v_{i,n} \]

向量内积的定义——投影

假设有一个数组：\(f[n]=n^2+n\)，\(n\)取整数，可以得到\(f[1]=2\)，\(f[2]=6\)，\(f[3]=12 \cdots\cdots\)
让该数组中\(n\)的间隔逐渐密集，可以得到\(f[1]=2\)，\(f[1.1]=2.31\)，\(f[1.2]=2.64 \cdots\cdots\)
如果让\(n\)的细分越来越小，直到无穷小？
密集的极限就是\(n\)完全连续，得到连续函数\(f(x)=x^2+x\)

函数就是无穷维的数组！（线性代数角度理解积分变换的重中之重）

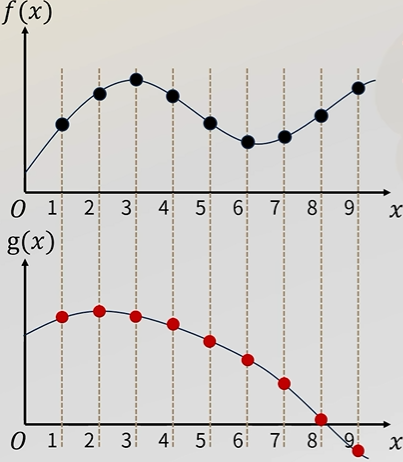
把函数当向量看，按照计算两个向量的内积（点乘）计算

\[\langle f(x),g(x)\rangle\approx f(1)g(1)+f(2)g(2)+\cdots+f(9)g(9)+\cdots \]

把这个函数上的点加密：

\[\langle f(x),g(x)\rangle\approx f(0.5)g(0.5)+f(1)g(1)+\cdots+f(9)g(9)+\cdots \]

这样会得到更加精确的函数内积，但这样取点越密，内积越大不对，实际上应该把每个相乘值乘上区间大小：

\[\langle f(x),g(x)\rangle\approx \frac{1}{2}(f(0.5)g(0.5)+f(1)g(1)+\cdots+f(9)g(9)+\cdots) \]

无穷维向量的投影

当函数上的点取的足够密集，实质上就是在计算两个函数间的投影
根据从离散到连续，求和到积分的思想，得到：

\[u_{(v_{i})}=\sum_{n=1}^{k}u_{n}v_{i,n} \]

向量内积——投影

\[\langle f(x),g(x)\rangle=\int_{-\infty}^{+\infty}f(x)g(x) \mathrm{d}x \]

函数内积——两个无穷维向量的投影

不要想成两个函数相乘，而是理解为对应点的值相乘再求和的极限形式

\[\langle f(x),g(x)\rangle\approx f(1)g(1)+f(2)g(2)+\cdots+f(n)g(n)+\cdots \]

\[\langle f(x),g(x)\rangle\approx0.01(f(0.01)g(0.01)+f(0.02)g(0.02)+\cdots+f(0.01n)g(0.01n)+\cdots \]

当取值密度趋向于无穷大，得到积分形态

函数的坐标变换——积分变换

按照之前的点乘坐标变换公式类比：

\[\frac{\langle f(x),g(x)\rangle}{\text{这是一个数}}=\int_{-\infty}^{+\infty}\frac{f(x)}{\text{原函数}}\cdot\frac{g(x)}{\text{一个基函数}}\mathrm{d}x \]

但现在只计算了原函数在一个基函数上的投影，因函数是无穷维的向量，所以如果希望用投影坐标复原原函数，那我们也必须在无穷多个基函数上求投影

\[\frac{F(\omega)}{\text{像函数}}=\int_{-\infty}^{+\infty}\frac{f(x)}{\text{原函数}}\frac{g(x,\omega)}{\text{正交函数组}}\mathrm{d}x \]

这就是函数的坐标变换——积分变换

既然像函数包含了原函数的所有坐标，那自然可以用像函数去复原原函数

\[\frac{f(x)}{\text{原函数}}= \int_{-\infty}^{+\infty} \frac{F(\omega)}{\text{像函数}} \frac{g(x,\omega)}{\text{正交函数组}}\mathrm{d}\omega \]

像函数\(F(\omega)\)其实就是一个坐标集合

复数、复变函数的内积问题

在实数空间内，上述公式成立，但在复数空间中，向量的内积等于一个向量与另一个向量的共轭进行点乘
一个向量和自身点乘，结果应该是这个向量模长的平方：

\[a\cdot a=\|a\|^{2} \]

假设不乘共轭，假设\(a=1+i\)，计算它和自身的点乘：

\[a\cdot a=(1+\mathrm{i})(1+\mathrm{i})=2\mathrm{i}\neq2 \]

只有乘共轭时，结果等于模长的平方：

\[a\cdot a^{*}=(1+\mathrm{i})(1-\mathrm{i})=1-\mathrm{i}^{2}=2=\|a\|^{2} \]

因此在复空间计算向量和函数内积时，默认对一个函数取共轭：

\[\langle f(x),g(x)\rangle=\int_{-\infty}^{+\infty}f(x)\cdot g^{*}(x) \mathrm{d}x \]

在复空间中，积分变换的形式为：

\[\frac{F(\omega)}{\text{像函数}}=\int_{-\infty}^{+\infty}\frac{f(x)}{\text{原函数}}\frac{g^{*}(x,\omega)}{\text{正交函数组}}\mathrm{d}x \]

这里是求向量的投影，所以要加上共轭

\[\frac{f(x)}{\text{原函数}}= \int_{-\infty}^{+\infty} \frac{F(\omega)}{\text{像函数}} \frac{g(x,\omega)}{\text{正交函数组}}\mathrm{d}\omega \]

这里是求向量的线性组合，所以不用加共轭

这个坐标变换，或者说积分变换有什么用? 我们究竟要用什么正交函数组作为基函数?

微分方程

物理学与工程学涉及的许多系统都是动力学系统，描述工具是微分方程

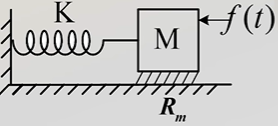
【1】弹簧-质量-阻尼 力学系统

\[\begin{gathered} f\left(t\right)-\mathrm{K}x-\mathrm{R}_{\mathrm{m}}v=\mathrm{M}a \\ f(t)-\mathrm{K}x-\mathrm{R}_{\mathrm{m}}\frac{\mathrm{d}x}{\mathrm{d}t}=\mathrm{M}\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}} \\ \mathrm{M}\frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}}+\mathrm{R}_{\mathrm{m}}\frac{\mathrm{d}x}{\mathrm{d}t}+\mathrm{K}x=f(t) \end{gathered}\]

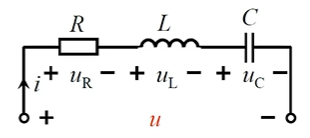
【2】电容-电阻-电感 电学系统

\[\begin{gathered} i=C \frac{du_{C}}{dt}\quad u_{R}=Ri=RC \frac{du_{C}}{dt}\quad u_{L}=L \frac{di}{dt}=LC \frac{\mathrm{d}^{2}u_{C}}{\mathrm{d}t^{2}} \\ LC \frac{\mathrm{d}^{2}u_{C}}{\mathrm{d}t^{2}}+RC \frac{\mathrm{d}u_{C}}{dt}+u_{C}=U \end{gathered}\]

都是类似的二阶常系数微分方程

差分and微分，求和and积分

差分就是对一个向量（数列）求后一项和前一项的差，求和就是前\(n\)项和
举个例子，有一串数组，22，17，16，14，17，18
依次用后一项减前一项得到差值：-5，-1，-2，3，1
这个操作实际上可以用矩阵达到：

import numpy as np

list_ex = np.array([22, 17, 16, 14, 17, 18])

# 创建一个差分矩阵
# 矩阵的形状为 (n, n)，用于计算相邻元素的差
n = len(list_ex )
diff_matrix = np.zeros((n, n))

# 填充差分矩阵
for i in range(n):
    diff_matrix[i, i] = -1      
    if i < n-1:
        diff_matrix[i, i+1] = 1  

print('Difference Matrix:\n', diff_matrix)

# 计算差分
list_diff = diff_matrix @ list_ex 

print("Original array:", list_ex )
print("Difference value:", list_diff)

Difference Matrix:
 [[-1.  1.  0.  0.  0.  0.]
 [ 0. -1.  1.  0.  0.  0.]
 [ 0.  0. -1.  1.  0.  0.]
 [ 0.  0.  0. -1.  1.  0.]
 [ 0.  0.  0.  0. -1.  1.]
 [ 0.  0.  0.  0.  0. -1.]]
Original array: [22 17 16 14 17 18]
Difference value: [ -5.  -1.  -2.   3.   1. -18.]

把数组与Difference Matrix相乘，去掉Difference value的最后一项即可
Difference Matrix是一个对角线上全为-1，右上对角线全为1，其余全为0的矩阵

再举一个例子，数组85，200，160，100，60，75，求前\(n\)项和：
逐项求和我们可以得到：85，285，445，545，605，680
也可以用矩阵达到这个操作：

import numpy as np

list_ex = np.array([85,200,160,100,60,75])

n = len(list_ex )
sum_matrix = np.zeros((n, n))

# 填充求和矩阵
for i in range(n):
    j = 0     
    while i >= j:
        sum_matrix[i, j] = 1  
        j += 1

print('Sum Matrix:\n', sum_matrix)

# 计算求和
list_sum = sum_matrix @ list_ex 

print("Original array:", list_ex )
print("Sum value:", list_sum)

Sum Matrix:
 [[1. 0. 0. 0. 0. 0.]
 [1. 1. 0. 0. 0. 0.]
 [1. 1. 1. 0. 0. 0.]
 [1. 1. 1. 1. 0. 0.]
 [1. 1. 1. 1. 1. 0.]
 [1. 1. 1. 1. 1. 1.]]
Original array: [ 85 200 160 100  60  75]
Sum value: [ 85. 285. 445. 545. 605. 680.]

我们知道求导本质上就是在无限密集情况下的差分，积分本质上就是在无限密集情况下的求和
又已知差分和求和都是矩阵，而函数本质上是无穷维的向量
那么求导和积分，本质上就是无穷维的矩阵：

求导和积分矩阵的特征向量

矩阵作用在向量上，不一定会导致向量方向改变。矩阵作用在某一些向量上时，向量方向不变，只有长度变化，这些向量称为矩阵的特征向量。

\[Ax=\lambda x \]

对于特征向量来说，矩阵作用等于数乘。
那么如果求导跟积分都是矩阵，二者的特征向量是什么？
显然是指数：

\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\mathrm{e}^{st}\right)=se^{st},\quad\int\mathrm{e}^{st} \mathrm{d}t=\frac{1}{s}e^{st}+C \]

当\(s\)为复指数\(s=\sigma+j\omega\)时，（用\(j\)避免与电流\(i\)弄混）

\[\Large \mathrm{e}^{st}=\mathrm{e}^{(\sigma+j\omega)t}=\mathrm{e}^{\sigma t}\mathrm{e}^{j\omega t}=\mathrm{e}^{\sigma t}(\cos\omega t+j\sin\omega t) \]

注意这里用到了欧拉公式：

\[e^{ix}=\cos x+i \sin x \]

三角函数和复指数的关系

基于欧拉公式：

\[e^{j\omega t}=\cos \omega t+j \sin \omega t \]

\[e^{-j\omega t}=\cos \omega t-j \sin \omega t \]

可以得到：

\[\cos \omega t = \frac{1}{2}(e^{j\omega t} + e^{-j\omega t}) \]

\[\sin \omega t = \frac{1}{2j}(e^{j\omega t} - e^{-j\omega t}) \]

基于三角函数辅助角公式：

\[\sin (\omega t+\varphi)=\cos \varphi \sin \omega t+\sin \varphi \cos \omega t \]

可以得到其复指数形式：

\[\begin{aligned} \sin (\omega t+\varphi) & =\frac{\cos \varphi}{2 j}\left(\mathrm{e}^{j \omega t}-\mathrm{e}^{-j \omega t}\right)+\frac{\sin \varphi}{2}\left(\mathrm{e}^{j \omega t}+\mathrm{e}^{-j \omega t}\right) \\ & =\frac{\sin \varphi-j \cos \varphi}{2} \mathrm{e}^{j \omega t}+\frac{\sin \varphi+j \cos \varphi}{2^{\circ}} \mathrm{e}^{-j \omega t} \end{aligned}\]

对于实数三角函数，在复指数形式上，在频率为\(\omega\)的点和频率为\(-\omega\)的点，振幅相等，相位相反。

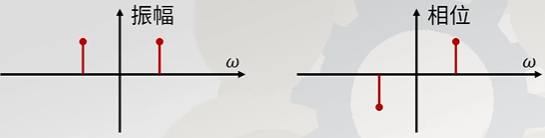
特征向量有什么用？

对于特征向量，矩阵作用相当于数乘；而求导和积分的运算是线性的：

\[\frac{df(x)}{dt}+\frac{dg(x)}{dt}=\frac{d[f(x)+g(x)]}{dt} \]

\[a\frac{df(x)}{dt}+b\frac{dg(x)}{dt}=\frac{d[af(x)+bg(x)]}{dt} \]

求导和积分的特征向量（特征函数）是复指数；
如果我们把一个函数表示为复指数的组合，那么对这个函数做求导和积分这样的复杂运算就可简化为代数运算，线性微分方程都变成代数方程。

用特征函数解微分方程

例1：

\[\frac{dx}{dt}+3x=0 \]

既然求导的特征函数是复指数，那么可以假设解为\(e^{{s_i}t}\)的线性组合，因为只有特征函数才能做到求导后形状不变，可以与\(3x\)（数乘）相消。然后我们把所有的\(s_i\)都找到，那么就可以知道原方程的解了。
假设其中一个解\(x=e^{st}\)，代入原方程得到：

\[se^{st}+3e^{st}=0 \]

由于\(e^{st} \neq 0\)，两边消掉得特征方程：

\[s+3=0,\quad s=-3 \]

这个方程没有多余的解了，因此得到原微分方程的解：

\[x=Ce^{-3t} \]

例2：

\[\frac{d^2x}{dt^2}+2\frac{dx}{dt}+2x=0 \]

根据上述同样的道理，假设其中一个解\(x=e^{st}\)，代入原方程得到：

\[s^2e^{st}+2se^{st}+2e^{st}=0 \]

由于\(e^{st} \neq 0\)，两边消掉得特征方程：

\[s^2+2s+2=0 \]

此时解变成复数了！

\[s_1=-1+j,\quad s_2=-1-j \]

也就是说，我们找到的两个线性无关的解为：

\[x_1=e^{(-1+j)t},\quad x_2=e^{(-1-j)t} \]

使用线性变换：

\[x'_1 = \frac{1}{2}(x_1+x_2)=e^{-t}cos t \]

\[x'_2 = \frac{1}{2j}(x_1-x_2)=e^{-t}sin t \]

可以得到方程的通解为：

\[x=C_1x'_1+C_2x'_2=e^{-t}(C_1cost+C_2sint)=Ae^{-t}sin(t+\varphi) \]

这个解是一个衰减振荡的形式

例3：

\[\frac{d^2x}{dt^2}+4\frac{dx}{dt}+4x=0 \]

假设其中一个解\(x=e^{st}\)，代入原方程得到：

\[s^2e^{st}+4se^{st}+4e^{st}=0 \]

由于\(e^{st} \neq 0\)，两边消掉得特征方程：

\[s^2+4s+4=0 \]

此时解存在重根，易知其中一个解为\(s=-2\)，此时需要使用一些手段找到另一个“消失的解”
假设\(x_1=e^{s_1t}, \quad x_2=e^{s_2t}\)是某线性微分方程的两个解
那么\(\Large x = \frac{e^{s_1t}-e^{s_2t}}{s_1-s_2}\)也应当是该微分方程的解（线性组合）
当\(s_1-s_2 \to 0\)时，趋向于重根状态
假设\(s_1 = s_2 + \Delta\)，取极限状态下：

\[\lim_{\Delta \to 0} \frac{e^{s_1t}-e^{s_2t}}{s_1-s_2} = \lim_{\Delta \to 0} \frac{e^{s_2 t}e^{\Delta t} - e^{s_2 t}}{\Delta} = \lim_{\Delta \to 0} e^{s_2 t} \frac{e^{\Delta t} - 1}{\Delta}(\frac{0}{0}) = \lim_{\Delta \to 0} e^{s_2 t} \cdot \left( \frac{1 + \Delta t - 1}{\Delta} \right) = te^{s_2 t} \]

也就是说在有重根状态下，一个解为\(x_1=e^{s_1t}\)，另一个解为\(x_2=te^{s_1t}\)
原微分方程通解：

\[x = Ae^{-2t} + Bte^{-2t} \]

用正弦函数作为正交基

周期函数可以表示为具有相同周期的复指数函数的线性组合
且这些函数两两正交归一：

\[\frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} e^{j m\omega t} e^{-j n \omega t} \, dt = 0 \quad \text{(} \omega = \frac{2\pi}{T}, \, m \neq n, \, m, n \in \mathbb{N} \text{)} \]

\[\frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} e^{j n\omega t} e^{-j n \omega t} \, dt = 1 \quad \text{(} \omega = \frac{2\pi}{T}, \, n \in \mathbb{N} \text{)} \]

注意这里是复函数求内积，是一个函数乘另一个函数的共轭

周期函数的频率分解——傅里叶级数

假定我们有一个周期函数\(f(t)\)，该函数具备周期\(T\)，
即频率为\(f_0=\frac{1}{T}\)，\(\omega_0=\frac{2\pi}{T}=2\pi f_0\)
我们希望找到这个函数在复指数基函数下每个频率\(f_0,2f_0,3f_0,\cdots,nf_0\)上的投影，怎么做？

\[F(n)=\left\langle f(t),\mathrm{e}^{jn2\pi f_{0}t}\right\rangle=\frac{1}{T}\int_{T}f(t)\mathrm{e}^{-jn2\pi f_{0}t}\ \mathrm{d}t \]

（周期函数求内积必须求单位周期内的结果）
现在假定我们知道了这个函数在复指数基下每个频率的投影坐标，如何复原原函数？

\[f(t)=F(0)+F(1)e^{j2\pi f_{0}t}+F(-1)e^{-j2\pi f_{0}t}+F(2)e^{j4\pi f_{0}t}+F(-2)e^{-j4\pi f_{0}t}+\cdots \]

\(n\)有正频率、负频率，用求和符号表示：

\[f(t)=\sum_{-\infty}^{+\infty}F(n)e^{jn2\pi f_{0}t} \]

求傅里叶级数的系数：（函数内积）

\[F(n)=\frac{1}{T}\int_{T}f(t)\mathrm{e}^{-jn2\pi f_{0}t}\ \mathrm{d}t \]

用傅里叶级数的系数复原原函数：（线性组合）

\[f(t)=\sum_{-\infty}^{+\infty}F(n)e^{jn2\pi f_{0}t} \]

再次用欧拉公式即可把以上公式转换为三角函数表达形式：

\[a_{0}=\frac{1}{T}\int_{T}f(t)\ \mathrm{d}t\quad a_{\mathrm{n}}=\frac{1}{T}\int_{T}f(t)\mathrm{cos}(n2\pi f_{0}t)\ \mathrm{d}t\quad b_{\mathrm{n}}=\frac{1}{T}\int_{T}f(t)\mathrm{sin}(n2\pi f_{0}t)\ \mathrm{d}t \]

\[f(t)=a_{0}+\sum a_{n}\cos(n2\pi f_{0}t)+\sum b_{n}\sin(n2\pi f_{0}t) \]

傅里叶变换公式推导

把\(F(n)\)和\(f(t)\)两公式合并：

\[f(t)=\sum_{n=-\infty}^{+\infty}\left(\frac{1}{T}\int_{T}f(t)\mathrm{e}^{-jn2\pi f_{0}t}\ \mathrm{d}t\right)e^{jn2\pi f_{0}t}=\sum_{n=-\infty}^{+\infty}\left(\int_{T}f(t)\mathrm{e}^{-jn2\pi f_{0}t}\ \mathrm{d}t\right)e^{jn2\pi f_{0}t}\cdot f_{0} \]

当函数周期逐渐变大，\(T\to\infty,f_{0}\to\mathrm{d}f\)，频率由离散的\(f_0\)变为连续的\(f\)，上式化为积分：

\[f(t)=\int_{-\infty}^{+\infty}\left(\int_{-\infty}^{+\infty}f(t)\mathrm{e}^{-j2\pi ft}\ \mathrm{d}t\right)e^{j2\pi ft}\mathrm{d}f \]

也就是把\(f(t)\)投影到一个连续的复指数函数上去，然后得到它的连续的正交基下的坐标是多少
令\(\omega = 2\pi f\)代入：

\[f(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\left(\int_{-\infty}^{+\infty}f(t)\mathrm{e}^{-j\omega t}\ \mathrm{d}t\right)e^{j\omega t}\mathrm{d}\omega \]

中间的括号内，把\(f(t)\)投影到不同频率上的这个，叫做频谱/频域，\(F(j\omega)\)或\(F(\omega)\)
傅里叶正变换：（负号来源是求共轭）

\[F(j\omega)=\int_{-\infty}^{+\infty}f(t)\mathrm{e}^{-j\omega t}\ \mathrm{d}t \]

傅里叶反变换：（\(2\pi\)来源是在\(d\omega\)和\(df\)之间转换得到的，这个系数放正反变换都行）

\[f(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(j\omega)e^{j\omega t}\mathrm{d}\omega \]