音速，马赫数和马赫锥

1、音速

音速也叫声速，声波在媒质（介质）中传播的速度。

• 声音的传播过程：物体震动会使得空气的压力时高时低，而使得空气分子产生疏、密变化，并由分子间的碰撞运动向外扩散出去。
• 声波是纵波：声波在传递时，空气分子的振动方向和波的传递方向是相同的，我们把这种波叫做"纵波"。
• 音速与介质的性质和状态有关。在压缩性小的介质中音速大于在压缩性大的介质中的音速。
• 声波一定要有介质才能传递出去，如果在真空状态，声波没有了传播的媒质，就无法听到声音了。

音速计算公式：
假设在汽缸中活塞自静止状态有一个突然的加速\(du\)；
活塞的加速运动产生一个压力波；并以速度\(c\)向右传播。

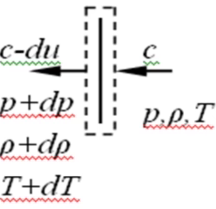
将坐标固定在音波上，选取控制体：

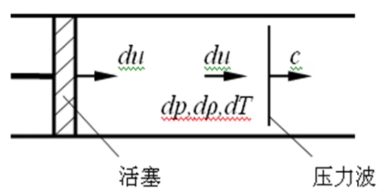
由连续性方程：

\[\rho cA=(\rho+d \rho)(c-du)A \]

略去小量\(d\rho du\)得到

\[du=\frac{d\rho}{\rho}c \]

由动量方程：

\[[p-(p+dp)]A=\rho Q[(c-du)-c] \]

由于\(Q=cA\)，上式简化：

\[-dpA=-\rho cAdu \]

\[du=\frac{dp}{\rho c} \]

比对两式，整理后得音速公式：

\[\frac{dp}{\rho c}=\frac{d\rho}{\rho}c => c=\sqrt{\frac{dp}{d\rho}} \]

关于音速的讨论

1. 音速体现了物质的可压缩性，越不容易压缩的物体，声音的传播越快
   在音速公式
   $$c=\sqrt{\frac{dp}{d\rho}}$$
   中，使密度发生\(d\rho\)改变所需的力\(dp\)越大，说明流体越不容易压缩，同时音速\(c\)越大

2. 声音的传播过程是一个等熵过程
   由等熵过程关系式，有
   $$p=C\rho^k => \frac{dp}{d\rho}=Ck\rho^{k-1}=k\frac{p}{\rho}$$
   得到
   $$c=\sqrt{k\frac{p}{\rho}}=\sqrt{kRT}$$
   对20°C的空气而言，由于\(k=1.4,R=287J/(kg\cdot K)\)，得到音速为
   \(c = \sqrt{1.4\times287\times293}=343m/s\)

   注：声音的传播不是等温过程

3. 不要把流体质点的运动与声音的传播相混淆

4. 不要把声音的传播过程跟气体流动过程相混淆

2、马赫数

马赫数定义是流速与音速之比

\[Ma=\frac{u}{c} \]

\[Ma \begin{cases} <1, & \text {亚音速流} \\ \approx1, & \text{跨音速流} \\ >1, & \text{超音速流}\end{cases} \]

亚音速和超音速流动的区别

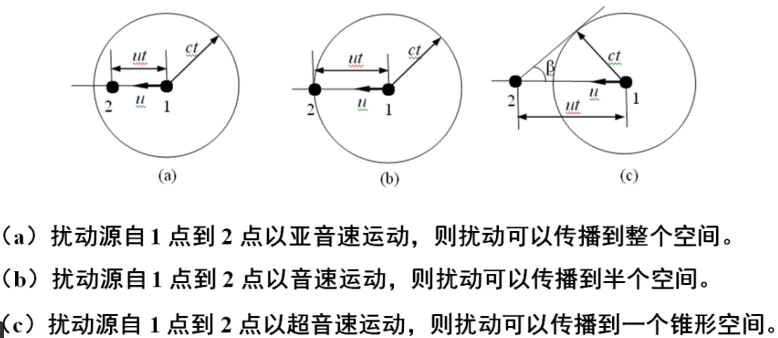
马赫锥

当波源运动速度高于波速时，波面的包络面呈圆锥状，称为马赫锥

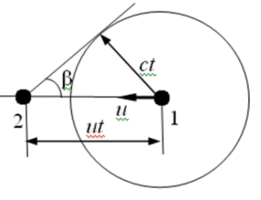
特点:扰动所能波及的区域限于一圆锥区域以内，这圆锥是一系列扰动球面的包络面，称为马赫锥;圆锥的半顶角称为马赫角。

\[sin\beta=\frac{ct}{ut}=\frac{1}{Ma} \]