NOIP算法初步笔记（1）——高精度计算（C语言描述）

一、定义

高精度运算，是指参与运算的数(加数，减数，因子……）范围大大超出了标准数据类型（整型，实型）能表示的范围的运算。

 

例如，求两个20000位的数的和。这时，就要用到高精度算法了。

 

本笔记中是常规做法思路，不含结构体定义类型bigint的方法。

 

二、高精度加（减）法

1.典型例题

 

 

2.编程思路

（1）首先要解决的就是存储200 位整数的问题。显然，任何C/C++固有类型的变量都无法保存它。最直观的想法是可以用一个字符串来保存它。字符串本质上就是一个字符数组，因此为了编程更方便，我们也可以用数组unsigned an[200]来保存一个200 位的整数，让an[0]存放个位数，an[1]存放十位数，an[2]存放百位数……

（2）那么如何实现两个大整数相加呢？方法很简单，就是模拟小学生列竖式做加法，从个位开始逐位相加，超过或达到10 则进位。也就是说，用unsigned an1[201]保存第一个数，用unsigned an2[200]表示第二个数，然后逐位相加，相加的结果直接存放在an1 中。要注意处理进位。另外，an1 数组长度定为201，是因为两个200 位整数相加，结果可能会有201 位。

（3）实际编程时，不一定要费心思去把数组大小定得正好合适，稍微开大点也无所谓，以免不小心没有算准这个“正好合适”的数值，而导致数组小了，产生越界错误。

3.代码实现

#include <stdio.h>
#include <string.h>
#define MAX_LEN 200
int an1[MAX_LEN+10];
int an2[MAX_LEN+10];
char szLine1[MAX_LEN+10];
char szLine2[MAX_LEN+10];
int main(void)
{
scanf("%s", szLine1);
scanf("%s", szLine2);
int i, j;
memset( an1, 0, sizeof(an1));
memset( an2, 0, sizeof(an2));
int nLen1 = strlen( szLine1);
for( j = 0, i = nLen1 - 1;i >= 0 ; i --)
an1[j++] = szLine1[i] - '0';
int nLen2 = strlen(szLine2);
for( j = 0, i = nLen2 - 1;i >= 0 ; i --)
an2[j++] = szLine2[i] - '0';
for( i = 0;i < MAX_LEN ; i ++ )
{ an1[i] += an2[i]; //逐位相加
if( an1[i] >= 10 )
{ //看是否要进位
an1[i] -= 10;
an1[i+1] ++; //进位
}
}
for( i = MAX_LEN; (i >= 0) && (an1[i] == 0); i -- ) ;
if(i>=0)
for( ; i >= 0; i--)
printf("%d", an1[i]);
else printf("0");
return 0;
}

 

三、高精度乘法

1.典型例题

 

 2.编程思路

（1）在程序中，用unsigned an1[200]和unsigned an2[200]分别存放两个乘数，用aResult[400]来存放积。计算的中间结果也都存在aResult中。aResult长度取400是因为两个200 位的数相乘，积最多会有400 位。an1[0], an2[0], aResult[0]都表示个位。

（2）计算的过程基本上和小学生列竖式做乘法相同。为编程方便，并不急于处理进位，而将进位问题留待最后统一处理。

3.样例举例

以 835×49 为例来说明程序的计算过程：

 

 

 

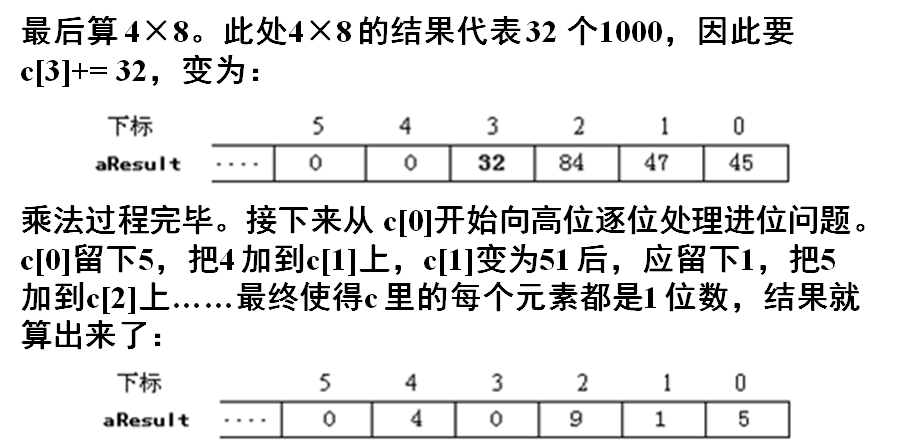
 4.总结规律：一个数的第i 位和另一个数的第j 位相乘所得的数，一定是要累加到结果的第i+j 位上。这里i, j 都是从右往左，从0 开始数。

 5.代码实现

#include <stdio.h>
#include <string.h>
#define MAX_LEN 200

int main(void)
{
int i, j;
int len1,len2;
int a[MAX_LEN+10],b[MAX_LEN+10],c[MAX_LEN*2+10];
char str1[MAX_LEN+10],str2[MAX_LEN+10];

for(i=0;i<MAX_LEN+10;i++) a[i]=b[i]=0;
for(i=0;i<MAX_LEN*2+10;i++) c[i]=0;
gets(str1); //按字符串形式读入第一个整数
gets(str2);
len1=strlen(str1);
for(j=0,i=len1-1; i>=0; i--)//把数字倒过来
a[j++]=str1[i]-'0';
len2=strlen(str2);
for(j=0,i=len2-1; i>=0; i--)//倒转第二个整数
b[j++]=str2[i]-'0';
for(i=0; i<len2; i++)//用第二个数乘以第一个数,每次一位
{
for(j=0; j<len1; j++)
c[i+j]+= b[i]*a[j]; //先乘起来,后面统一进位
}
for(i=0; i<MAX_LEN*2; i++)//循环统一处理进位问题
{
if(c[i]>=10)
{
c[i+1]+=c[i]/10;
c[i]%=10;
}
}
for(i=MAX_LEN*2; (c[i]==0)&&(i>=0); i--);//跳过高位的0
if(i>=0)
for(;i>=0;i--)
printf("%d", c[i]);
else
printf("0");
return 0;
}

四、高精度除法

1.典型例题

 

 2.编程思路

基本的思想是反复做减法，看看从被除数里最多能减去多少个除数，商就是多少。一个一个减显然太慢，如何减得更快一些呢？以7546 除以23 为例来看一下：开始商为0。先减去23 的100 倍，就是2300，发现够减3 次，余下646。于是商的值就增加300。然后用646 减去230，发现够减2 次，余下186，于是商的值增加20。最后用186 减去23，够减8 次，因此最终商就是328。

故核心是要写一个大整数的减法函数，然后反复调用该函数进行减法操作。 计算除数的10 倍、100 倍的时候，不用做乘法，直接在除数后面补0 即可。

 

3.代码实现（供参考）

#include <stdio.h>
#include <string.h>
#define MAX_LEN 200
char szLine1[MAX_LEN + 10];
char szLine2[MAX_LEN + 10];
int an1[MAX_LEN + 10]; //被除数, an1[0]对应于个位
int an2[MAX_LEN + 10]; //除数, an2[0]对应于个位
int aResult[MAX_LEN + 10]; //存放商，aResult[0]对应于个位
//长度为 nLen1 的大整数p1 减去长度为nLen2 的大整数p2
//结果放在p1 里，返回值代表结果的长度
//如不够减返回-1，正好减完返回 0
int Substract( int * p1, int * p2, int nLen1, int nLen2)
{
int i;
if( nLen1 < nLen2 )
return -1;
//判断p1 是否比p2 大，如果不是，返回-1
if( nLen1 == nLen2 )
{
for( i = nLen1-1; i >= 0; i -- )
{
if( p1[i] > p2[i] ) break; //p1>p2
else if( p1[i] < p2[i] ) return -1; //p1<p2
}
}
for( i = 0; i < nLen1; i ++ )
{ //要求调用本函数确保当i>=nLen2 时，p2[i] ＝ 0
p1[i] -= p2[i];
if( p1[i] < 0 )
{
p1[i]+=10;
p1[i+1] --;
}
}
for( i = nLen1 -1 ; i >= 0 ; i-- )
if( p1[i] )//找到最高位第一个不为0
return i + 1;
return 0;//全部为0，说明两者相等
}
int main()
{
int t, n;
scanf("%d", &n);
for( t = 0; t < n; t ++ )
{
scanf("%s", szLine1);
scanf("%s", szLine2);
int i, j;
int nLen1 = strlen( szLine1);
memset( an1, 0, sizeof(an1));
memset( an2, 0, sizeof(an2));
memset( aResult, 0, sizeof(aResult));
for( j = 0, i = nLen1 - 1;i >= 0 ; i --)
an1[j++] = szLine1[i] - '0';
int nLen2 = strlen(szLine2);
for( j = 0, i = nLen2 - 1;i >= 0 ; i --)
an2[j++] = szLine2[i] - '0';
if( nLen1 < nLen2 )
{
printf("0\n");
continue;
}
int nTimes = nLen1 - nLen2;
if(nTimes > 0)
{
for( i = nLen1 -1; i >= nTimes; i -- )
an2[i] = an2[i-nTimes];//朝高位移动
for( ; i >= 0; i--)//低位补0
an2[i] = 0;
nLen2 = nLen1;
}
for( j = 0 ; j <= nTimes; j ++ )
{
int nTmp;
//一直减到不够减为止
//先减去若干个 an2×(10 的 nTimes 次方)，
//不够减了，再减去若干个 an2×(10 的 nTimes-1 次方)，......
while( (nTmp = Substract(an1, an2+j, nLen1, nLen2-j)) >= 0)
{
nLen1 = nTmp;
aResult[nTimes-j]++; //每成功减一次，则将商的相应位加1
}
}
//输出结果，先跳过高位0
for( i = MAX_LEN ; (i >= 0) && (aResult[i] == 0); i -- );
if( i >= 0)
for( ; i>=0; i--)
printf("%d", aResult[i]);
else
printf("0");
printf("\n");
}
return 0;
}