RB-Tree(上)
RB-Tree(上)
RB-tree(红黑树)是加了平衡条件的二叉搜索树,需满足以下规则:
-
每个节点非红即黑。
-
根节点是黑色。
-
红节点不能有红色子节点(即不能连续红)。
-
从任一节点到其所有 NULL(叶端)路径上的黑节点数相同。
- 这些路径是指:从某个节点出发,往下走到“空指针”结束(即 NULL 节点)。
- 这些“NULL 节点”并不是真正存在于树中的实际节点,但在理论分析中,会将每个叶子节点的左右子指针(即指向 NULL)视为“虚拟叶子节点”。
- 这些“NULL”被视作黑色节点,这点在红黑树的定义中是默认的。
-
每个叶子节点(即 NULL 节点)都是黑色的。
-
在 红黑树的语境下:
-
NULL 被视作叶子节点,并且是黑色的。
-
一般来说红黑树中的“叶子节点”就是指的 NULL 节点(并不是没有孩子的真实节点)。
-
但有的时候是指实际节点,具体看情况。
-
-
新增节点设为红色,若违反规则需通过“变色”和“旋转”调整恢复平衡。
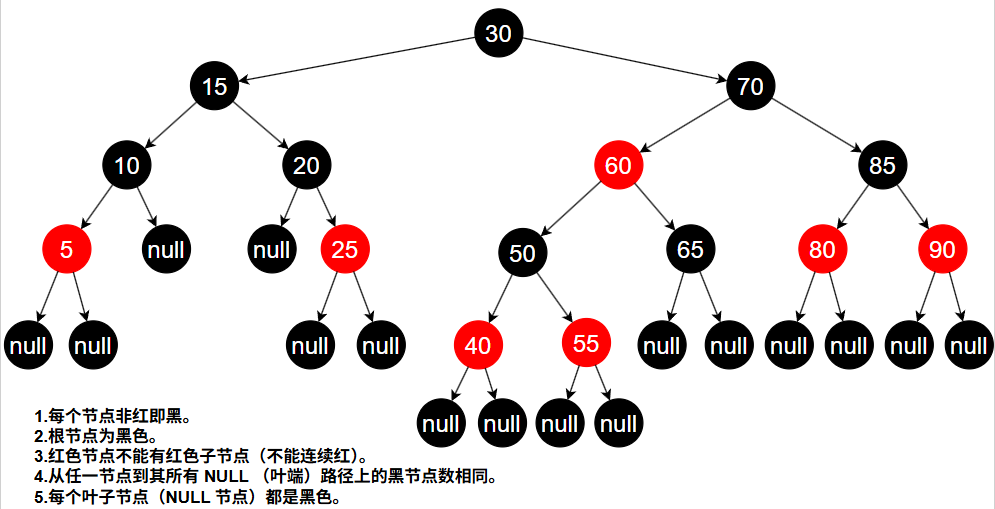
后续图示不再画出 NULL 节点。
AVL vs 红黑树的对比
| 特性 | AVL 树 | 红黑树 |
|---|---|---|
| 平衡条件 | 任一节点左右子树高度差 ≤ 1 | 任一路径黑节点数相同,不允许连续红 |
| 平衡“严格度” | 更严格(几乎是最平衡的) | 较宽松(可容忍部分不平衡) |
| 插入调整 | 可能需要多次旋转 | 最多一次旋转 + 多次变色 |
| 删除调整 | 较复杂,旋转多 | 简洁,最多三次旋转 |
| 查找效率 | 更快(因树更矮) | 略慢(树更高) |
| 应用场景 | 注重查找效率,如数据库索引 | 注重插入/删除效率,如操作系统、STL map/set |
插入节点
插入 3、8、35、75 后,都会违反红黑树的规则,因此需要调整结构。这些调整包括:旋转和变色,以恢复红黑树的五大规则(尤其是红红相连和黑高不一致的问题)。
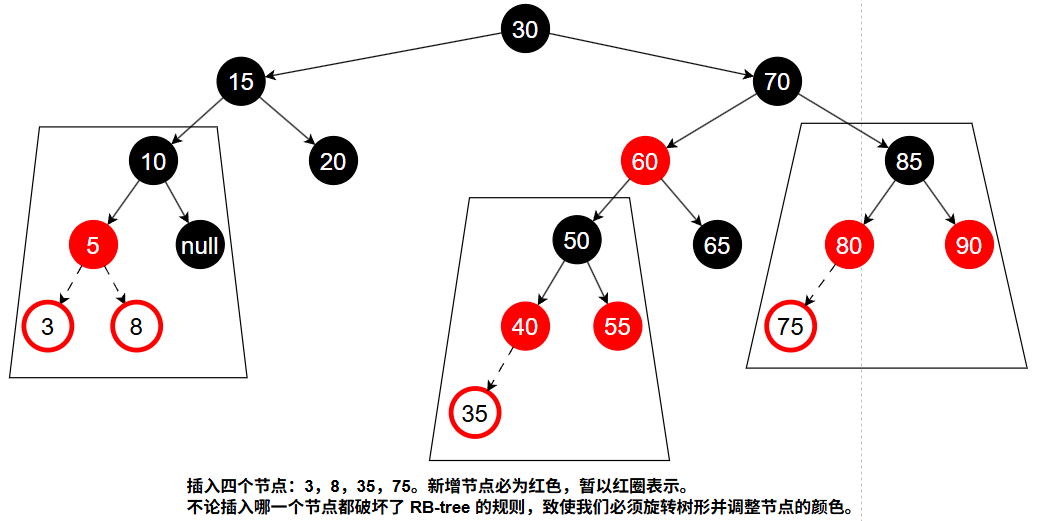
为便于讨论,我们为特定节点设定代称:
- 新插入节点为 X
- 父节点为 P
- 爷爷节点为 G
- 叔叔节点(P 的兄弟)为 S
- 曾爷爷节点为 GG
推论
- 由于按二叉搜索树规则,X 一定是叶节点;
- 根据红黑树规则 4,X 必须为红色;
- 若其父 P 也是红色,就违反了红黑树规则 3,必须进行调整(如果父节点是黑色,直接插入红色新节点,不需要任何旋转或染色操作;如果插入的就是根节点,那就把插入到红色节点变成黑色)。这时,G 必为黑色(因为原树满足红黑树规则)。
接下来根据插入节点 X 的位置 和叔叔节点 S、曾爷爷节点GG 的颜色,有三类典型处理情形。
情形一:插入的节点是根节点
处理方法:直接变黑。
情形二:插入节点的叔叔是黑色
叔叔节点 S 是黑色,且 X 是“外侧插入”
处理方法:单旋转加变色。
- 对 P 和 G 进行 一次单旋转
- 然后交换转轴 P 和旋转点 G 的颜色
这样就能重新满足红黑树的规则,尤其是规则 3(红色不能相邻)。这是最简单、最直接的一种调整方式。
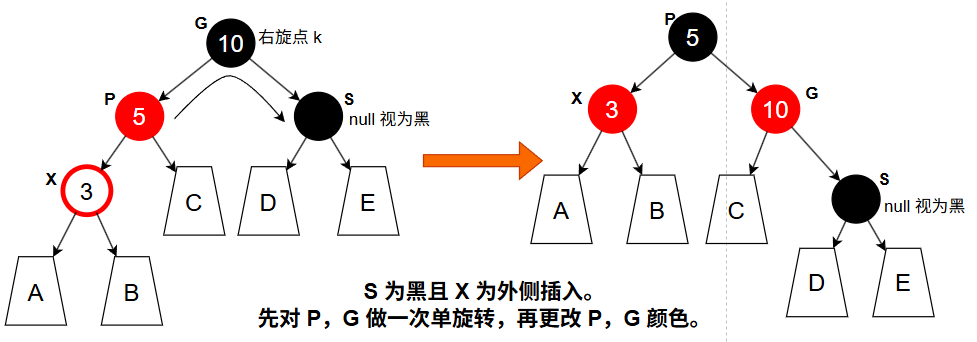
虽然此时可能出现子树高度差超过 1 的不平衡(如 A、B 为 null 而 D 或 E 非 null),但这无妨,因为红黑树的平衡要求本就比 AVL 树宽松。
经验表明,红黑树的平均搜索效率和 AVL 树几乎相同,实际效果很好。
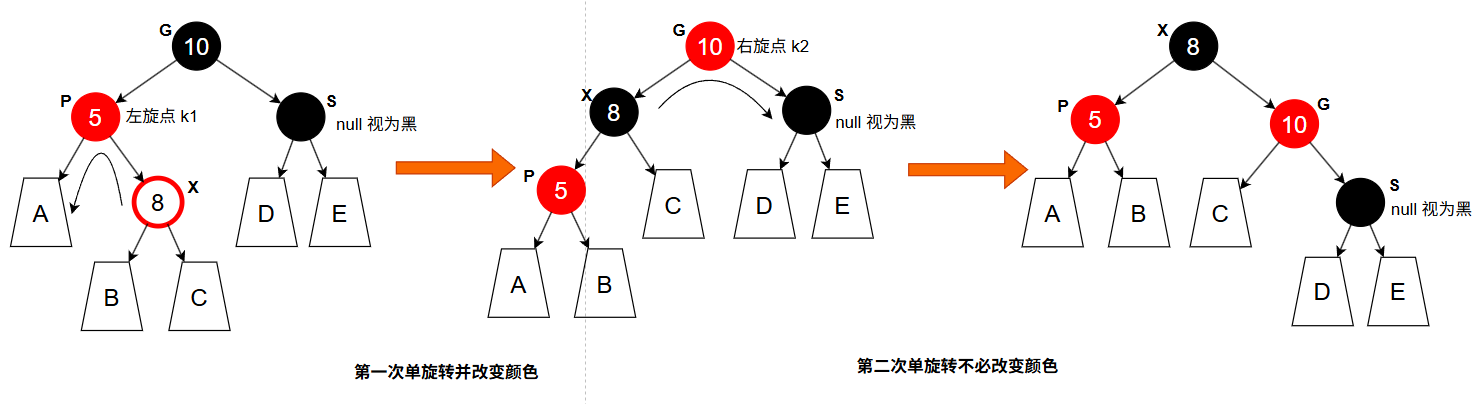
叔叔节点 S 是黑色,且 X 是“内侧插入”
处理方法:双旋转加变色。
- 对 P 和 X 进行 一次单旋转,并交换 G 和 X 的颜色
- 再对 G 进行 一次单旋转
情形三:插入节点的叔叔是红色
叔叔节点 S 是红色,且 X 是“外侧插入”
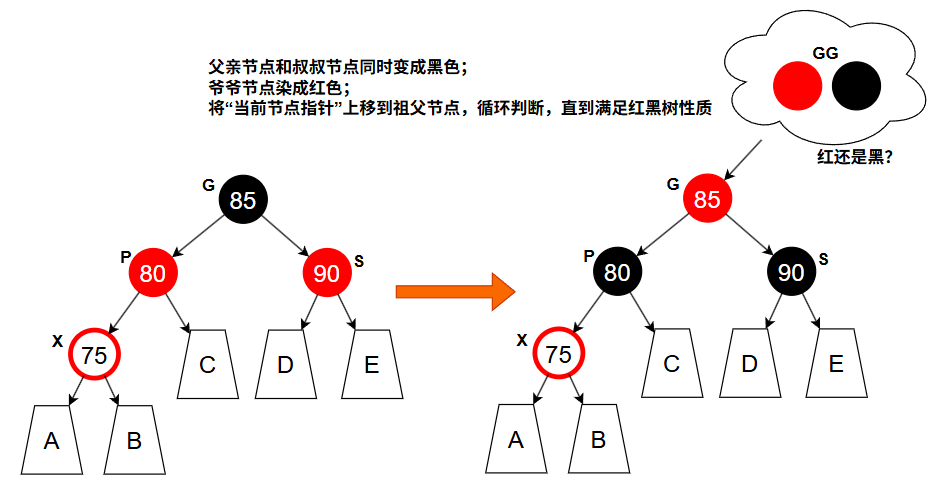
红黑树插入调整中,“叔叔节点 S 是红色”时,不论 X 是内侧插入还是外侧插入,这两种情况的处理方式是一样的——都是“重新染色并递归向上调整”。换句话说,叔叔是红色时,不旋转,只变色,并往上继续递归修正。
处理方法:
- 父节点和叔叔节点同时变为黑色
- 爷爷节点染成红色
- 将“当前节点指针”上移到爷爷节点,循环判断,直到满足红黑树性质(如根节点为黑,或没有连续红节点)
如果曾祖父 GG 是黑色,调整完成;若 GG 是红色,则把 G 当成新的插入节点,继续向上调整,直到没有连续红色父子节点为止。
小结
| 插入信息 | 处理办法 |
|---|---|
| 插入的节点是根节点 | 直接变黑。 |
| 插入节点的叔叔是黑色 | (LL,RR,LR,RL)旋转,然后变色。 |
| 插入节点的叔叔是红色 | 不旋转,只变色,把父亲节点,叔叔节点,爷爷节点都变色,然后当前节点指针上移到爷爷节点,循环判断。 |
Top-Down 插入优化策略
普通插入(Bottom-Up)
- 先一路找到插入位置,插入节点(红色)。
- 如果“父子皆红”才开始从插入点往上回溯修正。
- 回溯过程中可能会遇到多个节点需要旋转或变色。
- 问题:最坏情况下会一路递归到根,导致多次检查与栈操作。
Top-Down 插入
为了避免在插入过程中出现“父子节点同为红色”的情况,特别是当叔叔节点为红色时可能引发的向上颜色调整,可以采用一种 自顶向下(Top-Down) 的处理策略:
- 在向下走的过程中,一旦遇到某个节点 X 两个孩子都是红色,立刻:
- X 变红
- 两个孩子变黑
- 这样在到达插入位置之前,就已经打破了可能形成的“父子红冲突”。
- 新节点插入后,冲突范围被局限在很小的局部,通常只需要一次旋转(或者甚至不用)。
对比效果
逻辑本质
- 是同一个修正过程,只是把回溯改成了下行时的“预修正”。
- 所以它不会改变红黑树最终结构,只是改变调整的时机。
性能差别
- Bottom-Up:可能需要递归回溯 N 层(N 为树高度)。
- Top-Down:始终是 O(1) 栈空间(因为一路向下),没有显式回溯。
- 在需要频繁插入、且数据分布不平衡的情况下,Top-Down 的常数开销会小一些,尤其适合无递归的实现(例如在内核或嵌入式里)。
缺点
- 写法更复杂,要考虑沿途变色可能引起的旋转(尤其当父节点是红色时)。
- 有些情况下会多做一次颜色翻转(虽然不影响最终树形)。
这种变换能预先消除将来可能出现的红冲突,从而减少后续旋转和颜色调整的复杂度,也能避免向上递归调整,提升插入效率。它并不是“额外优化红黑树的平衡性质”,只是把调整从事后搬到事前,节省了回溯的栈操作,让插入过程可以一次从根到叶的线性遍历完成,适合要求无递归的实现。
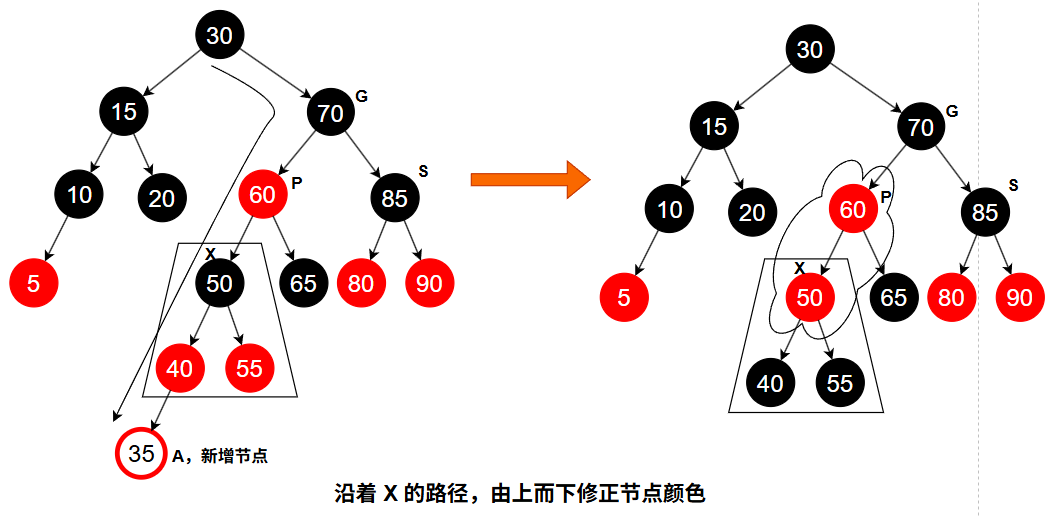
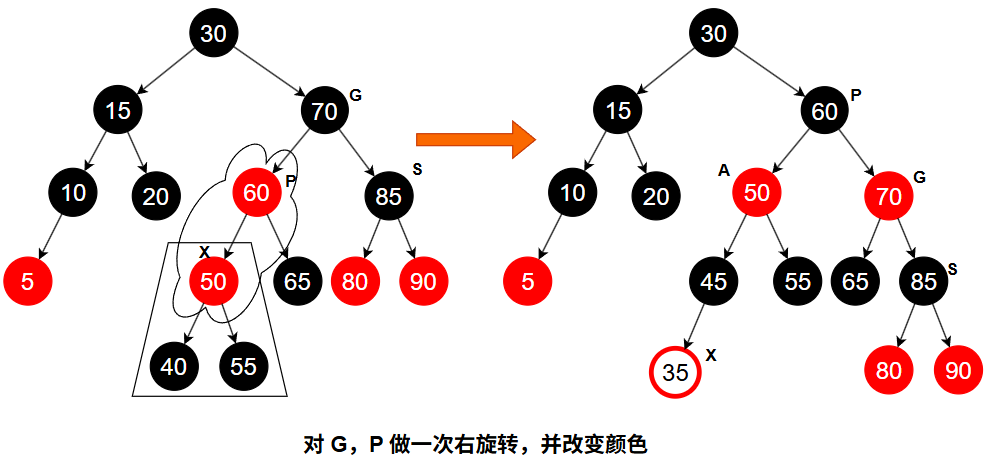
即使使用 Top-Down 插入法,在插入节点 A 的路径上先做了变色处理,但若插入 A 后,A 的父节点 P 是红色,仍会产生“父子皆红”的违规情况。此时:
- 若是“外侧插入”(A 和 P 同侧)→ 执行一次单旋转,并交换颜色。
- 若是“内侧插入”(A 和 P 异侧)→ 执行一次双旋转,并调整颜色。
完成这些操作后,红黑树性质恢复。接着,后续节点(如节点 35)插入就会很简单:
只需普通插入,或插入后配合一次简单的旋转即可。
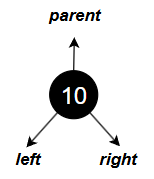
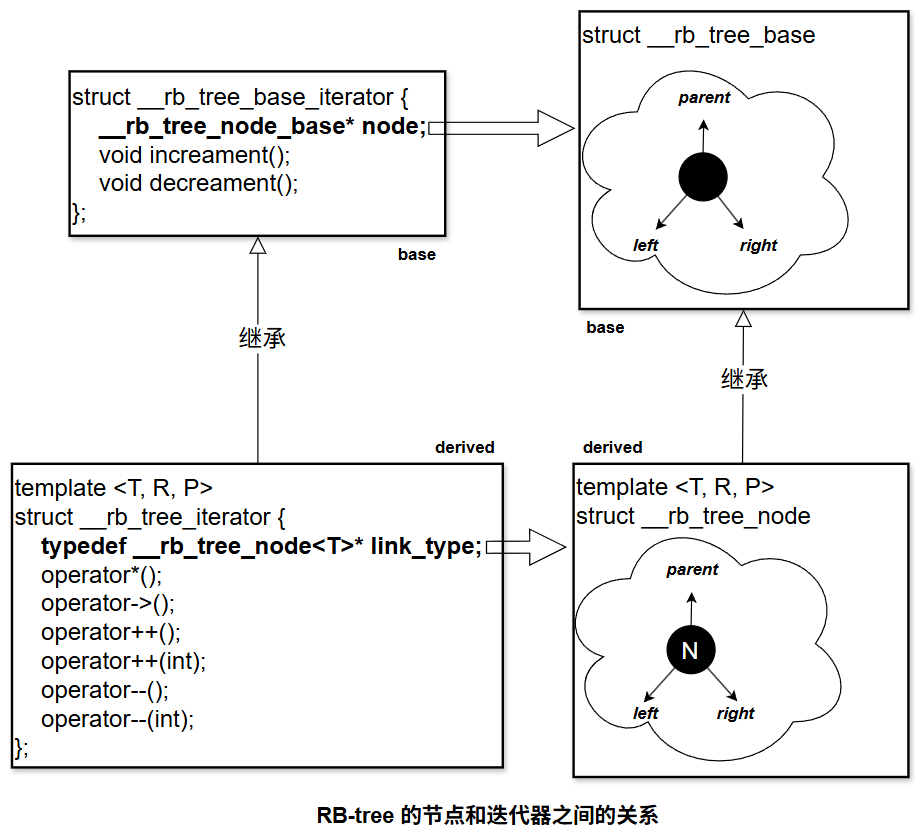
RB-tree 的节点设计
RB-tree 是具有红黑节点和左右子树的二叉搜索树。SGI STL 实现中采用双层节点结构,并设有 parent 指针,便于向上回溯。极值查找如 minimum()、maximum() 操作也非常简单高效。
// 定义颜色类型为 bool
typedef bool __rb_tree_color_type;
// 红色为 false (0),黑色为 true (1)
const __rb_tree_color_type __rb_tree_red = false;
const __rb_tree_color_type __rb_tree_black = true;
// 基础节点结构体,包含颜色、父子节点指针
struct __rb_tree_node_base {
typedef __rb_tree_color_type color_type; // 节点颜色类型(红或黑)
typedef __rb_tree_node_base* base_ptr; // 指向自身类型的指针别名
color_type color; // 节点颜色,非红即黑
base_ptr parent; // 指向父节点的指针(红黑树的操作常需要回溯父节点)
base_ptr left; // 指向左子节点的指针
base_ptr right; // 指向右子节点的指针
// 查找以 x 为根的子树中的最小值节点(一直往左走)
static base_ptr minimum(base_ptr x) {
while (x->left != 0) x = x->left;
// 一直向左走就能找到最小值
return x;
}
// 查找以 x 为根的子树中的最大值节点(一直往右走)
static base_ptr maximum(base_ptr x) {
while (x->right != 0) x = x->right;
// 一直向右走就能找到最大值
return x;
}
};
// 继承基础节点结构体,并添加 value 域(即模板值类型)
template <class Value>
struct __rb_tree_node : public __rb_tree_node_base {
typedef __rb_tree_node<Value>* link_type; // 指向自身类型的指针别名
Value value_field; // 存储的数据内容(节点的值)
};
- 红黑树节点由
__rb_tree_node_base提供通用结构,包括颜色和指针。 __rb_tree_node<Value>是模板化的节点,额外持有值字段value_field。minimum()和maximum()利用了二叉搜索树的特性,分别查找最小和最大值节点。
RB-tree 的迭代器
为了将 RB-Tree 实现为泛型容器,迭代器设计是关键,需支持以下操作:
- 类型分类(category)
- 前进(++)、后退(--)
- 提领(*)、成员访问(->)
SGI STL 采用了 双层结构 的设计:
- 节点:
__rb_tree_node继承自__rb_tree_node_base - 迭代器:
__rb_tree_iterator继承自__rb_tree_base_iterator
这种设计类似 slist,利于统一操作与灵活转换,也方便我们深入分析 RB-Tree 的行为和状态。
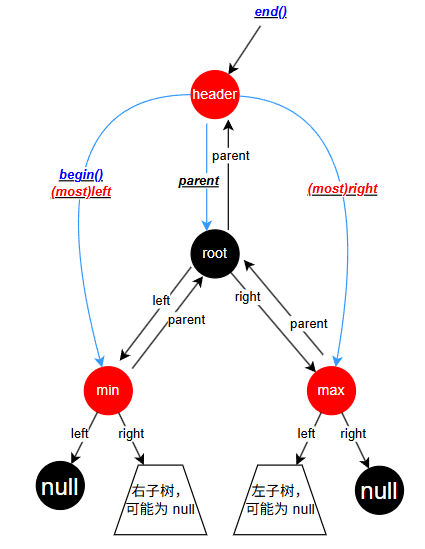
header 节点
header 的位置和作用
在 SGI STL 的 rb_tree 里,header 节点是一棵红黑树之外的特殊节点,它的结构是这样的:
header是基类__rb_tree_node_base类型的节点,它只包含最基础的指针和颜色信息,没有存储具体的值。- 普通的红黑树节点是
__rb_tree_node,它继承自__rb_tree_node_base,并额外存储了数据字段(Value)。
主要作用:
- 保存根节点指针(
header->parent):header->parent指向树的真正根节点。 - 保存最小节点指针(
header->left):header->left指向树中的最小节点,方便begin()常数时间返回。 - 保存最大节点指针(
header->right):header->right指向树中的最大节点,方便end()前一个迭代器的查找。 - 充当
end()迭代器的 node:迭代器到达最后一个节点的下一个位置时,node会指向header。
RB-Tree 迭代器特性与前后移动操作
- 属于双向迭代器,不支持随机访问。
- 提领(
*)与成员访问(->) 与list类似。 - 前进操作
operator++()会调用基类的increment() - 后退操作
operator--()会调用基类的decrement()
前后移动都遵循 二叉搜索树的中序遍历规则,实现上对根节点处理有些特殊技巧。
RB-tree 基础迭代器结构:
struct __rb_tree_base_iterator {
typedef __rb_tree_node_base::base_ptr base_ptr;
typedef bidirectional_iterator_tag iterator_category;
typedef ptrdiff_t difference_type;
base_ptr node; // 当前迭代器指向的节点指针
// 中序遍历的后继节点(++ 操作)
void increment() {
if (node->right != 0) {
// 情况 1:当前节点有右子树
// 后继是右子树中最左节点
node = node->right;
while (node->left != 0)
node = node->left;
} else {
// 情况 2:当前节点无右子树
// 向上回溯,寻找第一个祖先节点,使当前节点是该祖先的左子节点
base_ptr y = node->parent;
while (node == y->right) {
node = y;
y = y->parent;
}
// 退出循环时:
// 情况 2.1:y 是第一个使 node 成为其左子节点的祖先,
// 此时循环前的 node 的直接后继就是 y
// 情况 2.2:y 是 header(哨兵),循环后的 node 是根节点,
// 循环前的 node 实际是最大值节点,
// 经过下面的判断后,node 被设为 header,表示迭代器到达 end()
if (node->right != y)
node = y;
}
}
// 中序遍历的前驱节点(-- 操作)
void decrement() {
// 情况 1:当前迭代器指向 header(end())
// header 颜色为红色,且其父的父节点是 header 本身
if (node->color == _rb_tree_red && node->parent->parent == node) {
// 前驱是树中最大节点,位于 header->right
node = node->right;
} else if (node->left != 0) {
// 情况 2:当前节点有左子树
// 前驱是左子树中最右节点
base_ptr y = node->left;
while (y->right != 0)
y = y->right;
node = y;
} else {
// 情况 3:当前节点无左子树
// 向上回溯,找到第一个祖先节点,使当前节点是该祖先的右子节点
base_ptr y = node->parent;
while (node == y->left) {
node = y;
y = y->parent;
}
// y 是中序遍历的前驱节点
node = y;
}
}
};
RB-tree 正规迭代器结构(继承基层迭代器):
template <class Value, class Ref, class Ptr>
struct __rb_tree_iterator : public __rb_tree_base_iterator {
// 迭代器中元素的类型
typedef Value value_type;
// 解引用时返回的引用类型,可能是 Value& 或 const Value&
typedef Ref reference;
// 迭代器指针类型,可能是 Value* 或 const Value*
typedef Ptr pointer;
// iterator 和 const_iterator 类型定义,方便使用
typedef __rb_tree_iterator<Value, Value&, Value*> iterator;
typedef __rb_tree_iterator<Value, const Value&, const Value*> const_iterator;
typedef __rb_tree_iterator<Value, Ref, Ptr> self; // 当前迭代器类型自身别名
typedef __rb_tree_node<Value>* link_type; // 节点指针类型
// 构造函数
__rb_tree_iterator() {} // 默认构造,节点为空
__rb_tree_iterator(link_type x) { // 通过节点指针构造迭代器
node = x;
}
__rb_tree_iterator(const iterator& it) { // 通过非 const 迭代器构造 const 迭代器
node = it.node;
}
// 解引用操作符:通过迭代器访问节点的值
reference operator*() const {
return link_type(node)->value_field; // 节点的值成员变量,一般叫 value 或 value_field
}
#ifndef __SGI_STL_NO_ARROW_OPERATOR
// 箭头操作符,返回指向节点值的指针,方便通过迭代器访问成员
pointer operator->() const {
return &(operator*());
}
#endif
// 前置 ++ 运算符:移动到中序遍历的下一个节点
self& operator++() {
increment(); // 调用基类或成员函数完成节点跳转
return *this;
}
// 后置 ++ 运算符:移动到下一个节点,返回递增前的迭代器副本
self operator++(int) {
self tmp = *this; // 复制当前迭代器
increment();
return tmp; // 返回递增前的迭代器
}
// 前置 -- 运算符:移动到中序遍历的前一个节点
self& operator--() {
decrement(); // 调用基类或成员函数完成节点跳转
return *this;
}
// 后置 -- 运算符:移动到前一个节点,返回递减前的迭代器副本
self operator--(int) {
self tmp = *this; // 复制当前迭代器
decrement();
return tmp; // 返回递减前的迭代器
}
};
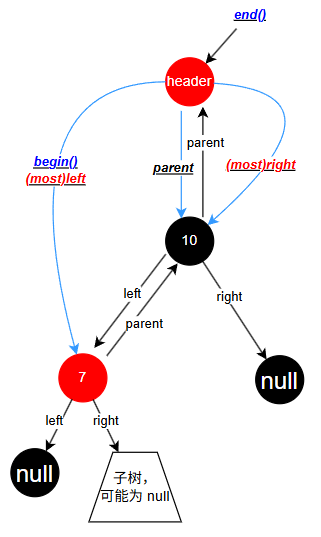
increment() 的状况 2.2:
当迭代器指向的是整棵树的最大节点,执行 ++ 时会指向 header,也就是 end()。
decrement() 的状况 1:
当迭代器是 end()(即指向 header)时,执行 --,实际返回的是最大节点(最右节点)。
RB-tree 的数据结构
下面是红黑树(RB-tree)的定义简述:
- 使用专属的空间配置器,每次分配一个节点大小的内存。
- 定义了多种类型,用于管理整棵红黑树的数据结构。
- 包含一个仿函数(functor),用于比较节点的大小,保证树的有序性。
- 提供了若干成员函数,用于插入、删除、查找等操作。
这些设计保证了红黑树的灵活性和高效性。
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc = allocator>
class rb_tree {
protected:
typedef void* void_pointer;
typedef __rb_tree_node_base* base_ptr; // 基础节点指针类型,指向红黑树节点基类
typedef __rb_tree_node<Value> rb_tree_node; // 红黑树节点具体类型,存储Value数据
typedef simple_alloc<rb_tree_node, Alloc> rb_tree_node_allocator; // 节点内存配置器,用于节点的分配和释放
typedef __rb_tree_color_type color_type; // 节点颜色类型,红或黑
public:
// 公开类型定义,方便外部访问
typedef Key key_type; // 键的类型
typedef Value value_type; // 节点存储值的类型
typedef value_type* pointer; // 指向值的指针类型
typedef const value_type* const_pointer; // 指向常量值的指针类型
typedef value_type& reference; // 值的引用类型
typedef const value_type& const_reference; // 常量值引用类型
typedef rb_tree_node* link_type; // 节点指针类型
typedef size_t size_type; // 容器大小类型
typedef ptrdiff_t difference_type; // 差值类型
protected:
// 内存管理相关函数
// 分配一个新的节点内存
link_type get_node() {
return rb_tree_node_allocator::allocate();
}
// 释放一个节点内存
void put_node(link_type p) {
rb_tree_node_allocator::deallocate(p);
}
// 创建节点(分配+构造)
link_type create_node(const value_type& x) {
link_type tmp = get_node(); // 先分配内存
__STLTRY {
construct(&tmp->value_field, x); // 构造节点数据部分
} __STL_UNWIND(put_node(tmp)); // 构造失败时释放内存
return tmp;
}
// 复制节点,复制值和颜色,但左右子节点置空
link_type clone_node(link_type x) {
link_type tmp = create_node(x->value_field); // 复制节点值
tmp->color = x->color; // 复制颜色
tmp->left = 0;
tmp->right = 0;
return tmp;
}
// 销毁节点(析构并释放内存)
void destroy_node(link_type p) {
destroy(&p->value_field);
put_node(p);
}
protected:
// 树的核心数据成员
size_type node_count; // 当前树中节点总数
link_type header; // 特殊节点,作为树的“头”,方便操作树结构
Compare key_compare; // 用于比较键值的仿函数
// 通过header节点访问红黑树中的重要节点:
// root节点、最左(最小)节点、最右(最大)节点
link_type& root() const { return (link_type&) header->parent; }
link_type& leftmost() const { return (link_type&) header->left; }
link_type& rightmost() const { return (link_type&) header->right; }
// 静态辅助函数,方便访问节点的成员指针和值
static link_type& left(link_type x) { return (link_type&)(x->left); }
static link_type& right(link_type x) { return (link_type&)(x->right); }
static link_type& parent(link_type x) { return (link_type&)(x->parent); }
static reference value(link_type x) { return x->value_field; }
static const Key& key(link_type x) { return KeyOfValue()(value(x)); }
static color_type& color(link_type x) { return (color_type&)(x->color); }
// 以上函数对 base_ptr 同样支持,方便类型转换和操作
// 查找子树的最小和最大节点
static link_type minimum(link_type x) { return (link_type)__rb_tree_node_base::minimum(x); }
static link_type maximum(link_type x) { return (link_type)__rb_tree_node_base::maximum(x); }
public:
// 迭代器类型定义,方便外部使用
typedef __rb_tree_iterator<value_type, reference, pointer> iterator;
private:
// 内部辅助函数声明
iterator __insert(base_ptr x, base_ptr y, const value_type& v);
link_type __copy(link_type x, link_type p);
void __erase(link_type x);
// 初始化树结构
void init() {
header = get_node(); // 分配header节点
color(header) = _rb_tree_red; // header颜色设为红,便于区分
root() = 0; // 空树时root为空
leftmost() = header; // header的left指向自己,表示空树
rightmost() = header; // header的right指向自己,表示空树
}
public:
// 构造函数,初始化空树,传入比较函数对象
rb_tree(const Compare& comp = Compare()) : node_count(0), key_compare(comp) {
init();
}
// 析构函数,清空树并释放header节点
~rb_tree() {
clear(); // 清空所有节点
put_node(header); // 释放header
}
// 访问器
// 返回比较函数对象
Compare key_comp() const { return key_compare; }
// 返回指向最小元素的迭代器
iterator begin() { return leftmost(); }
// 返回表示end()的迭代器(header节点)
iterator end() { return iterator(header); }
// 判断是否为空树
bool empty() const { return node_count == 0; }
// 返回节点数量
size_type size() const { return node_count; }
// 返回最大容量(通常是size_t最大值)
size_type max_size() const { return size_type(-1); }
// 插入接口(详细实现略)
// 保持节点值独一无二
pair<iterator, bool> insert_unique(const value_type& x);
// 允许节点值重复
iterator insert_equal(const value_type& x);
// ...
};
header节点是红黑树中一个特殊哨兵节点,用来简化树操作,比如空树时的根节点为空的情况等。KeyOfValue是一个仿函数,用来从Value中提取对应的Key,方便做键比较。- 内存管理使用
simple_alloc封装,负责节点内存分配与释放。 insert_unique和insert_equal分别对应不允许重复键和允许重复键的插入操作。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号