Trie树的应用,一道算法问题求解 问题分析
首先给大家看一下题目,题目出自 http://www.bianchengla.com/
原文如下:
Emergency 911
Alice 97 625 999
Bob 91 12 54 26
In this case, it’s not possible to call Bob, because the central would direct your call to the emergency line as soon as you had dialled the first three digits of Bob’s phone number. So this list would not be consistent.
- Input:
- The first line of input gives a single integer, 1 ≤ t ≤ 40, the number of test cases. Each test case starts with n, the number of phone numbers, on a separate line, 1 ≤ n ≤ 10000.
- Then follows n lines with one unique phone number on each line. A phone number is a sequence of at most ten digits.
- Output:
- For each test case, output “YES” if the list is consistent, or “NO” otherwise.
下面我对这道题目简单翻译一下,方便看英文不便的朋友:
给定一个电话号码的列表,来确定这些号码是否一致,一致的意思就是,这些号码中没有一个号码是另一个号码的前缀。
如下面的电话号码:
Emergency 911
Alice 97 625 999
Bob 91 12 54 26
在几个号码的例子中,我们不能呼叫Bob,因为当你输入Bob的电话号码前三位的时候,呼叫中心将会把你的呼叫转移到报警电话:911
输入:
第一行输入一个整数,1 ≤ t ≤ 40,测试用例的数量,每一个用例都会在另起一行的位置有一个整数n,1 ≤ n ≤ 10000。
接下来的每一行都是一个电话号码,每个电话号码最多10个字符。
输出:
如果一致,输出YES,否则输出NO
简单来说,这道题目的中心思想就是,给定一组字符串,我们来判断其中是否有两个字符串A和B,其中一个是否以另一个为起始。
比如 A = "1233455"
B = "1233"
这里,A以B起始,如果有这样的关系,我们就说,这组字符串是不一致的。
解决这个问题,有很多种方法,比如最直观的,就是通过几层循环的嵌套,逐个的比较各个字符串是否有这种关系。使用这种方法,虽然比较直观,但它的效率比较低下,大概估算了一下,遍历这个列表,就需要两层循环,然后进行字符串的比对又是一层循环。采用这种方式至少需要O(n3) 的时间复杂度。随着输入规模的增长,效率会越来越低。
类似这种问题,有一种结构非常适合,那就是Trie树,一般用在字典搜索等应用中。
关于Trie树,网上有很多现成的文章,所以这里就不详细说明了,只在下面简单介绍一下。有兴趣的朋友可以参考数据结构相关的资料。
根据我们的问题,假设现在有这几个电话号码:
1249
1395
1378
就会形成这样一颗Trie树:

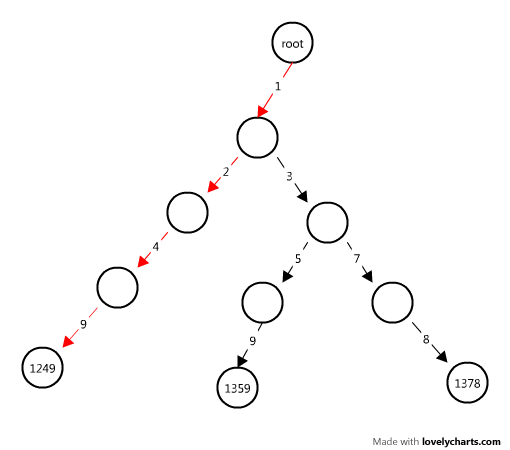
通过上面的图片,我们对Trie树有了一个比较直观的了解,由于我们的问题要处理的只是电话号码中的字符,所以每个字符可能的值只能是0-9,因此我们这里的Trie树,每个节点最多有10条边,分别对应数字0-9的匹配。
我们这里要做的主要有这两步:
1. 根据输入,将这组中的所有电话号码,构造成Trie树。
2. 遍历这颗Trie树,检查是否有被另一个字符串包含的字符串。
首先说第一步,构造Trie树不难理解,只是逐个分析输入字符串的每个字符,为它们构造相应的节点,还是以 "1249”,这个字符串为例,首先我们进入树的根节点,并找到字符串的第一个字符'1',先看一下根节点有没有边为'1'的子节点,如果有则遍历到这个节点,如果没有就创建该节点;然后我们遍历到边为1的那个子节点,并取到字符串的第二个字符'2',进行和上面相同的过程,直到取完整个字符串,并将最后一个节点标识为字符串的终结(这个对我们这道题很重要)。
接下来要进行第二步,检查是否有包含关系的字符串,这个过程非常简单,我们仔细观察一下我们上面Trie树,如果这组字符串没有包含关系,那么这颗树中只有叶子节点才会被标识为字符串的终结(在我们的Trie树中在这个节点上面写上相应的字符串,如上面图中的叶子节点),如果非叶子节点被标识为字符串终结,那么这颗树一定存在包含关系,从而证明这组电话号码是不一致的。相信这个应该不难理解,看看下面这幅图,在我们原有的Trie树中,又加入了另一个字符串"137",显然,它是包含于字符串"1378"的:
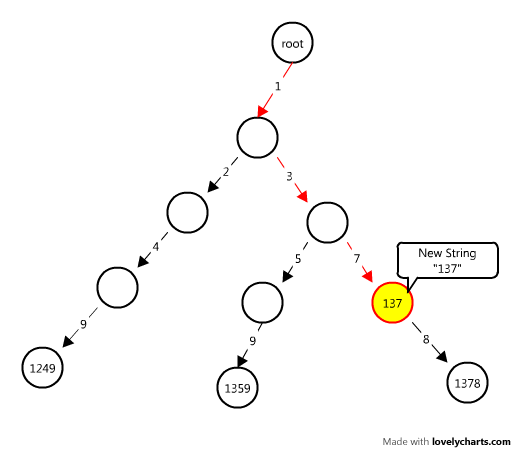
上图中,"137"与"1378",均在同一条路径上,明显可以看出"137"包含于"1378",这种情况下,较短的那个字符串一定是在非叶子节点上面结束的。
通过上面这两步,并结合Trie树结构,这个问题基本就解决了,我们可以看到无论是创建节点和遍历节点,都可以在线性的时间内完成,这样就大大的提高了运行的效率。不过使用Trie树来解决该问题,有一点不足的就是,这种数据结构比较消耗内存,这里我们只有0-9的10个数字,每个节点最多只会有10个子节点,如果字符集的规模再扩大的话,消耗的内存就会更高。当然提高了时间上的运行效率,一般情况下都会都空间上产生一些消耗,具体采用什么样的算法,也需要根据具体的需求而定。
这里给出了该问题求解的一个思路,在下一篇中将给出它的具体实现方式,感兴趣的朋友不妨先试试写一下这个程序,如果有更好的算法大家来一起交流![]() 。
。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号