省选集训—树上技巧选讲 by zdj

树链剖分的扩展方法

树链剖分一些扩展性质：

1. 基于重标号的深度优先搜索优化的树链剖分算法
2. 轻重边分治处理思想‘
3. 重边批量修改，轻边用了再查

NOI 轻重边

染色的方法比较神奇，我们考虑不这样处理。

其实还是相当于对于每个点以及其邻接点的转化，不妨让每个点代表其到父亲的边，并标记其是否是重边。

那么相当于给这条链上（不包括 lca） 赋值为 \(1\)，邻接点赋值为 \(0\)。

考虑标号时，先标记整条重链，然后从下往上/从上往下将链上的点的邻接点也标号。

这样就满足了一条重链除了链头之外，重链标号连续，重链的某个子段的邻接点标号连续。

那么就可以线段树暴力覆盖了，注意跳轻边的时候特别处理跳过去的重儿子。

集训队互测-简单树剖练习题

重链剖分，再用一个树状数组维护树上差分便于查找某个点的点权。

这样可以直接 \(O(\log n)\) 查到某条边边权。

我们考虑批量维护重边权值，而单独查询轻边权值

那么一次修改，重边权值批量变化 \(2k·|a_u-a_v|^m\)，差不变，可以线段树暴力打标记维护，仅有 \(O(\log n)\) 条重边需要单独单点修改

那么一次查询，只会查询 \(O(\log n)\) 条重边。

维护即可。

集训队互测-线段树与区间加

注意到一次操作在首次分裂成两半递归后，以左边的递归为例，每次走左儿子，那么就是给右儿子批量修改。

并且 \(a=\sum len·lz\)，所以这是不必要的，因此我们只需要维护 \(vb’·lz\)。

考虑 懒标记的下传，本质上是将每个点的懒标记变为到树根的懒标记的和

所以这启发我们不维护真实的懒标记值，而是维护每个点到树根的懒标记的和。

那么就相当于是子树加了（也就是往左走的给所有往左走时的右儿子子树加）

然后我们考虑怎么通过这个东西得到答案。

\(ans=\sum vb_i(lz_i-lz_{fa_i})=\sum lz_i(vb_i-vb_{lc}-vb_{rc})\)

这就行了。

可以重链剖分，然后先整体递归走左儿子非重儿子的左儿子，最后整体递归走右儿子非重儿子的右儿子。

这样我们可以保证：重链除了链头编号连续，重链上所有点的左非重儿子树编号连续，右非重儿子树编号连续。

因此可以 \(3\) 个区间表达一整个子树，接下来就是区间修改的事情了。

处理一车细节后可以通过。

树上杂题

CF1585G

显然的 SG 题目。

\(SG(u)=mex_{d=0}^{mnd}\lbrace b_d\rbrace\)，其中 \(b_d\) 定义为 \(\oplus_{v\in Subtree(u),d(u,v)=d+1}sg_v\)，注意可能这个点不存在。

根据长链剖分的相关结论，我们只需要快速计算仅有一个儿子的节点的 dp 值即可，且这本质上与在计算 \(son\) 的 dp 值后加入了一个 \(son\) 而已，可以直接 \(dp_u\leftarrow dp_{son}\)，然后继续向后枚举计算 mex。

至于有多个儿子的时候，我们只在乎其最浅儿子深度的这些点的 dp 值，如果可以合并这些结果就好了。

这是容易的，可以直接暴力合并，根据长链剖分，复杂度正确。
然后暴力计算就好了（SG值显然不会超过 \(2(mnd+1)\)）

CF772E

动态维护 \([1,i-1]\) 的虚树，现在考虑加入 \(i\)，一个很有意思的是，若询问 \(x,y\)，则回复可以让我们知道 \(i\) 是否在子树内，如果在，那么在 \(lca(x,y)\) 的哪个方向的子树也是知道的。

并且图三度化，那么可以点分治这个LCA的寻找，然后查找到 \(i\) 应该加入的位置。

细节比较多，需要注意实现。

永恒

考虑到 \(lcp\) 长度等价于 Trie 上 LCA 深度，那么如果可以计算出 Trie 树上每个节点的被计算次数就好了。

那么问题就变成了对于每个Trie树上的点 \(t\)，求所有的 \(x,y\)，满足 \(lca(b_x,b_y)=t\)，在原树上经过 \(x,y\) 的路径个数。如果 \(x,y\) 没有祖孙关系这将是容易的。

现在考虑转化为没有祖孙关系的问题，可以使用点分治，我们只需要单独处理当前分治中心对所有点的贡献，剩下的贡献都可以当作 \(sz_x·sz_y\)。

注意啊，这个 \(sz_x\) 是指原树上，断掉了 \(x\) 与当前点分治的那个父亲的边后的 \(sz\) 大小，需要特别说明。

那么这就容易了，将连通块内点建立虚树，然后暴力统计，至于 \(x,y\) 位于分治中心的同一个子树里的情况，可以再做一次进行容斥。

CF1930G

很唐啊，一直在想怎么在树上搞，但是事实说明计数题只需要充要条件，树形结果只是附加。

设 \(f_x\) 为以 \(x\) 为结尾的前缀最大值个数（\(x\) 是目前序列的最后一个）

目标 \(f_n\)。

考虑 \(f_x\to f_y\) 的条件是什么：

1. \(x<y\)，\(x\) 不小于 \(rt\to fa_y\) 的最大值。
2. 根到 \(x\) 的路径中，\(x\) 编号最大。
3. \(x\) 是 \(lca(x,y)\) 的 \(x\) 方向上子树里最大的点

可以考虑将每个点的儿子按照子树内编号最大值从小到大排序，然后做 \(dfs\)，这样每个点的有效时间都是一个时间段，在 dfs 的时候就可以求得部分点的失效时间，这样使用树状数组维护即可。

CF1876E

考虑一个特殊情况：外向树，这种情况每条边都可以赋值为一个颜色。

考虑将原图等效为一个外向树的图。

贪心地，如果我们定根将无向边全部变为外向边，考虑这时候的内向边会起到什么作用呢？

事实上就是将其与指向它的外向边染为同一个颜色，然后就等效为一个外向边了。

那么定根后的最大颜色数事实上还是外向边条数。

则这样可以快速换根求出答案，然后做一次 dfs 模拟进行染色就好了。

一个可能的疑问是如果我们找到了一个内向边，但是栈空了怎么办。

事实上这是不可能的，因为我们将两个点作为根的方案反转，只会影响这两个点之间的路径，因此最优的根，一定到每个点的路径上外向边不少于内向边，因此栈不可能为空。

CF1930H

首先答案是不在路径上的点的点权最小值。

我们问题化为将树进行两次标号，并使用这两次标号的结果将树上除掉这条路径的图划分为不超过 \(5\) 个区间。

使用入栈序和出栈序，画图不难发现。

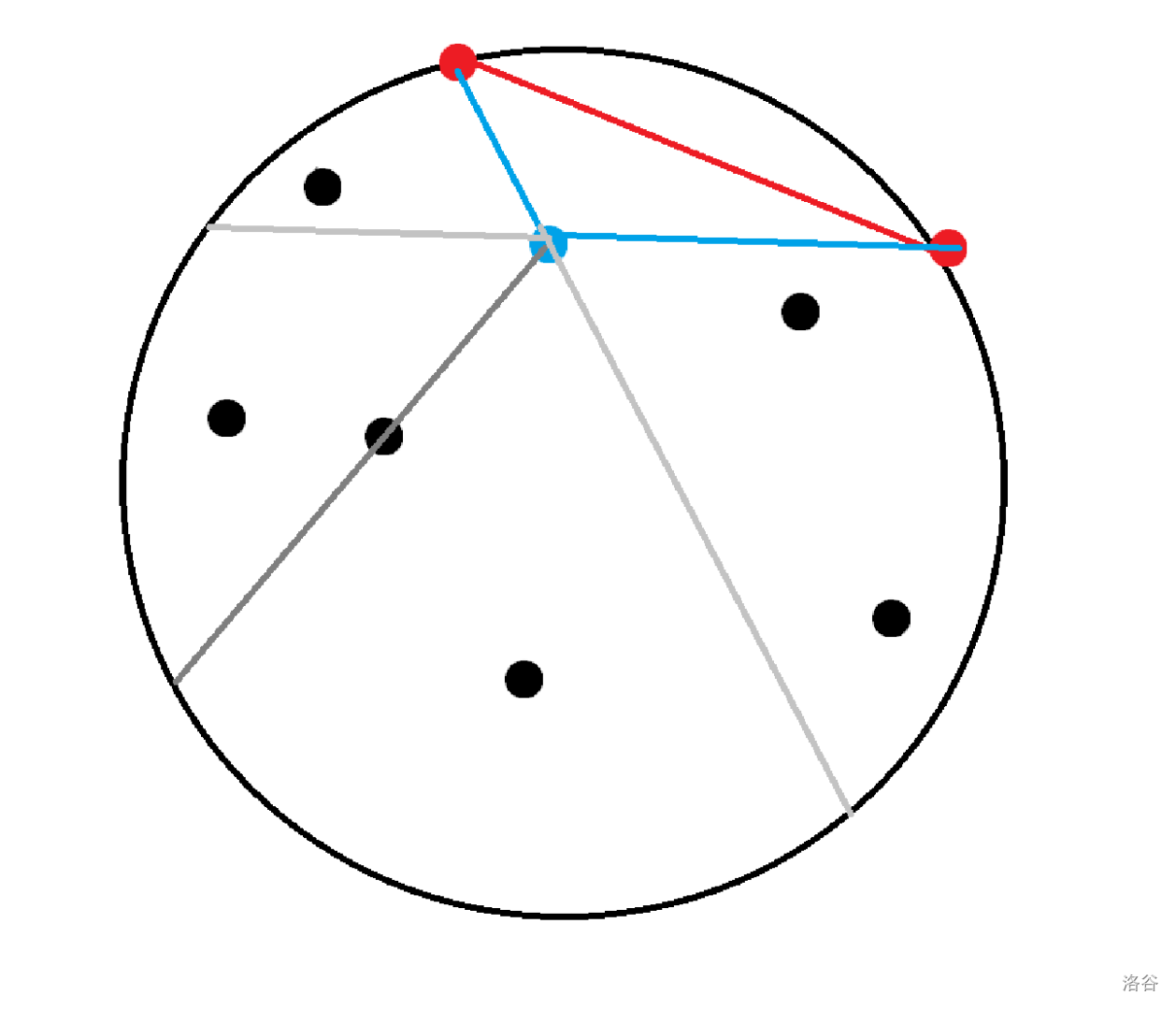
「CEOI2022」Drawing

可以有一个 \(O(n^2)\) 的暴力解法：任意定一个在凸包上的点作为根的代表点，然后 dfs 时，做极角排序，并按照各个儿子的 \(sz\) 在极角序里面划分，前 \(sz_1\) 个划给第一个子树，\(sz_1+1\sim sz_2\) 划给第二个子树……

并且第 \(sz_1\) 个钦定为第一个儿子的代表点，第 \(sz_2+sz_1\) 钦定为第二个儿子的代表点……递归即可解决。

这样做是 \(O(n^2\log n)\) 的，利用 nth-element 技术可以做到 \(O(n^2)\)。

优化划分过程，但是很遗憾的是用不了点分治（因为该点分治划分后分治中心并没有钦定）

一个神奇的想法是做链分治

递归处理，先拿出一整条重链，找到一个重链上的 \(mid\)，并将点集划分为断掉 \((mid,fa_{mid})\) 的两部分，两部分递归处理。

这样分治下去只有几种情况：当前点集，我知道链头的代表点/我知道链头和链底的代表点。

考虑将链底与链头的两个点取凸包上相邻的两个点，这样可以保证点集的划分。

接着我们如何确定 \(mid\) 呢？也就是保证 \((mid,fa_{mid})\) 无论 \(fa_{mid}\) 怎么取都不会导致相交。

那么取 \(mid\) 保证 \(mid,top,down\) 三点的三角形内不存在其他点，并将点集划分为按照 \(mid\) 极角排序（注意到这时候需要再特别预处理一下已经确定划分到左/右的点，保证 \(mid\) 是剩下的点的凸包）后的对应大小个。就可以保证无论 \(mid\) 怎么连，\((mid,fa_{mid})\) 与 \((mid,v),v\in Son(mid)\) 的边永远不会相交，并且两个点集也不可能再通过连边相交。

至于 \(mid\) 怎么取？首先从 \(up\) 极角序的对应 \(sz\) 个开始找，满足 \(up-down,mid-down\) 的夹角最小即可。

这样一定可以满足三角形内无点，且可以划分出对应大小个的点。

同时 \(mid\) 取这条重链的中点/带权中点都可以。