省选集训-模拟赛 3

A

\(2^n·n^2\) 的暴力枚举想必不用多说。

考虑暴力 dp，设 \(f_{i,S}\) 为 \([1,i]\) 里选了集合 \(S\) 的点，那么可以容易的 \(O(n)\) 扫描更新，做到 \(O(2^n·n)\)

注意到对于 \(f_{i,S}\) 以及更后面的状态而言，将 \(a_i\sim a_n\) 排序后的 \(b_1\sim b_{n-i+1},b_0=0,b_{n-i+2}=n+1\) 若已经选的数 \(x,y\) 满足 \(\exists i,b_{i-1}<x,y<b_i\)，则 \(x,y\) 是等效的。

这启发我们将 dp 状态重新定义为 \(f_{i,c_1,c_2,\dots }\)，表示选完 \([1,i]\) 后，在后面的这些段里面，已经选的数字落在每一段的数的个数。

这样看似很暴力，但是事实上可以分析：设当前有 \(m\) 段，\(l_1\sim l_m\)（左开右闭），而段长总和是 \(n\)，则状态数总和 \(\prod_{i=1}^ml_i\le \prod_{i=1}^m\overline{l}=(\frac{n}{m})^m\)

考虑求函数 \(f(x)=(\frac{n}{x})^x\) 的最值：

\[f(x)=e^{\ln f(x)}=e^{x\ln \frac{n}{x}}=(e^x)^{{\ln n-\ln x}} \]

该函数在 \(e\) 时取到最值，\((-\infty,e)\) 单调递增，\((e,+\infty)\) 单调递减，且 \(f(3)>f(2)\)，因此状态数最多是 \(O(n3^{\frac{n}{3}})\)，加上转移复杂度，实现精细可以做到 \(O(n^23^{\frac{n}{3}})\)

---

还存在一个折半法：考虑将前 \(26\) 个与后 \(9\) 个分治，按照后 \(9\) 个的范围将前 \(26\) 个划分为 \(9\) 段，其 \(2^{26}\) 种状态化简后并不多，将每个状态取最优的，再加上 \(2^9\times status\) 的枚举计算。

---

还存在一个抽象复杂度做法：可以基于 LIS/LDS 给出暴力枚举（在此基础上增加元素），而我们知道 \(\max(LIS,LCS)\ge \sqrt n\)，所以可以 \(2^{29}\) 左右。

---

B

考虑分治计算答案，设中间轴是 \(mid\)，我们考虑计算起点在 \([l,mid]\) 列中，终点在 \([mid+1,r]\) 列中。

容易发现，走回头路的情况只有一种：

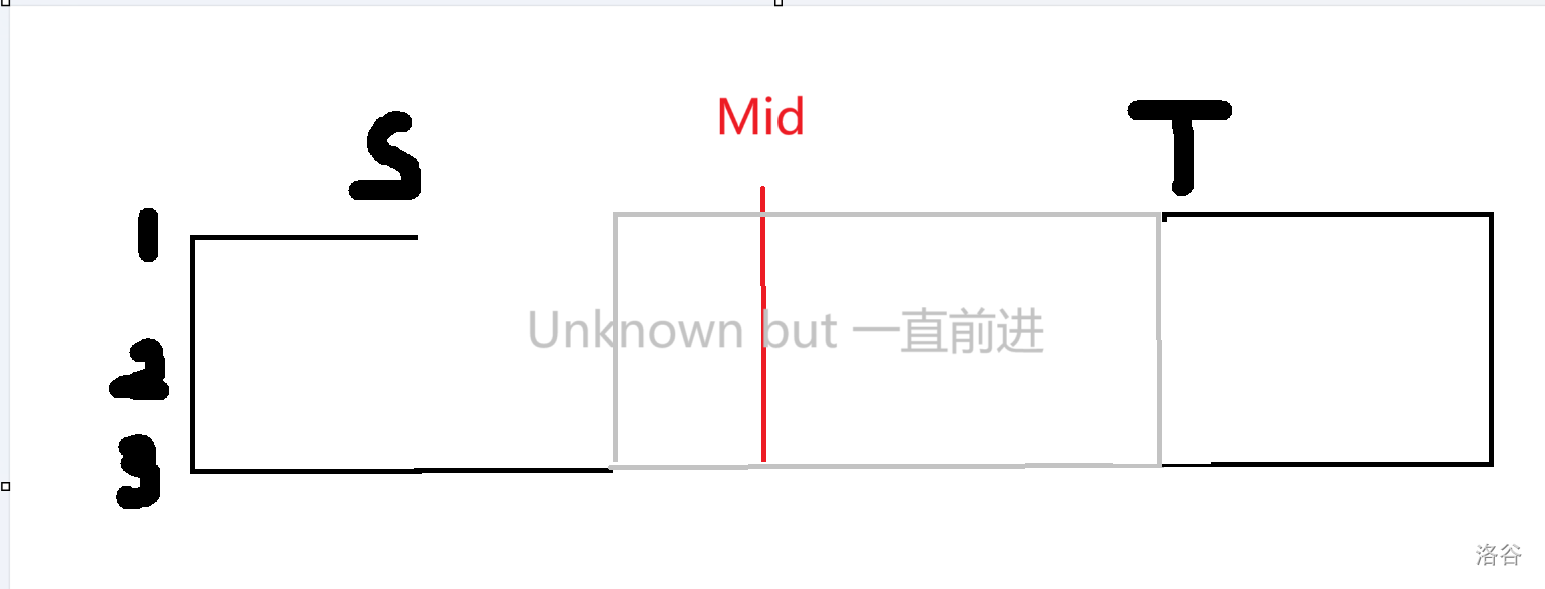
如果要走回头路，则必然是第一行与第三行之间转换，且 mid 左边至多一次，mid 右边至多一次。

而走回头路，最优的 U 字可以预处理（通过前缀和即可知晓，顺序扫一遍，每次相当于加入一条竖线，并给所有竖线加上若干权值）。

注意 U 字并不一定在 \([l,r]\) 范围内

那么现在我们就可以考虑计算了。

设 \(f_{i,j,k}\) 表示第 \(j\) 行第 \(k\) 列的元素到第 \(i\) 行 \(mid\) 列元素的最短路（\(k\le mid\) 不计算 \(val(i,mid)\)，\(k>mid\) 计算 \(val(i,mid)\)）

这个可以先简单 dp 不走回头路的情况（这一定不会超出 \([l,r]\) 范围，可以 \(O(n(r-l))\) 解决），然后再用 U 去更新决策

那么 \((x,y)\to (p,q)\) 的最短路可以描述为：

\[\min(f_{0,x,y}+f_{0,p,q},f_{1,x,y}+f_{1,p,q},f_{2,x,y}+f_{2,p,q}) \]

而我们需要计算的就是对于所有的 \(x\in [0,n-1],y\in [l,mid],p\in [0,n],q\in[mid+1,r]\) 这样的值的和。

其实挺容易的，我们考虑枚举 \(0/1/2\) 谁取到最小并计算。

我们优先让 \(0\) 取最小，其次让 \(1\) 取最小，最后让 \(2\) 取最小，这里是边界上的问题，稍加讨论即可。

那么以 0 取最小为例，事实上是：

\[\begin{cases} f_{0,x,y}+f_{0,p,q}\le f_{1,x,y}+f_{1,p,q}\\ f_{0,x,y}+f_{0,p,q}\le f_{2,x,y}+f_{2,p,q}\\ \end{cases} \implies \begin{cases} f_{0,x,y}-f_{1,x,y}\le f_{1,p,q}-f_{0,p,q}\\ f_{0,x,y}-f_{2,x,y}\le f_{2,p,q}-f_{0,p,q}\\ \end{cases} \]

这是一个二维偏序问题，容易计算。

因此本题 \(O(nm\log^2 m)\) 解决了。

---

C

做法很多啊，根据 lcm 有决策单调性（四边形不等式）等等。

讲一个独一无二的反贪做法：我们考虑从 \(i\to i+1\)。

首先每个 \(b\) 相同的肯定先取 \(c\) 最大的。

考虑在 \(i\) 的最优解中删掉 \(S\)，并加入 \(T\)，满足 \(1+\sum_{x\in S}b_x=\sum_{x\in T}b_x\)

且由于最优性，若存在 \(X\subseteq S,Y\subseteq T,\sum_{x\in X}b_x=\sum_{y\in Y}b_y\)，则可以同时去掉集合 \(X,Y\)。

根据这样的限制条件打表发现只有 27 个方案，枚举取最优即可。