任意多边形面积的计算

1-原理介绍

       原理论述1：

       书中给出定理：任意多边形的面积可由任意一点与多边形上依次两点连线构成的三角形矢量面积求和得出。

       矢量面积=三角形两边矢量的叉乘。

       如下图：

 

按定理，多边形面积由P点与A-G的各顶点连接所构成的三角形矢量面积构成，假定多边形顶点坐标顺序为A-G，逆时针为正方向，则有如下结论：

PAB,PBC,PCD均为顺时针，面积为负；

PDE，PEF，PFG，PGA均未逆时针，面积为正；

但无论正负，均可通过P点与顶点连线的矢量叉乘完成，叉乘结果中已包含面积的正负。

        原理论述2：

设Ω是m边形(如下图)，顶点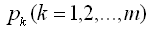沿边界正向排列，，坐标依次为

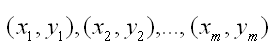
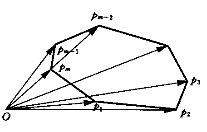
建立Ω的多边形区域向量图。

由图知坐标原点与多边形任意相邻的两个顶点构成一个三角形，而三角形的面积可由三个顶点构成的两个平面向量的外积求得。

任意多边形的面积公式

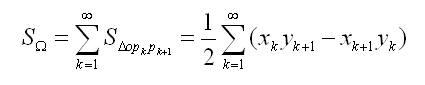
多边形计算公式的计算和原点的选取没有关系，通常可以选点（0,0）或者多边形的第一个点（这个时候比较直观了，看起来就是把多边形分成一个个三角形和加起来，读者自己可以画个图）就可以了。

2-程序设计

采用C++的vector（动态数组）存储顶点坐标。

为方便计算，直接将P点定为原点（0,0），则多边形顶点xy坐标即为向量在xy上分量。

循环计算多边形顶点坐标每一点与下一点之间的线段，及这两点与P连线的矢量所围成的三角形面积。

计算面积的函数代码如下：

C++的实现

iArea=iArea+(vecPoly[iCycle].x*vecPoly[(iCycle+1) % iCount].y-vecPoly[(iCycle+1) % iCount].x*vecPoly[iCycle].y);
int intAreaCalc(vector<myPoint> &vecPoly)
{
    int iCycle,iCount,iArea;
    iCycle=0;
    iArea=0;
    iCount=vecPoly.size();

    for(iCycle=0;iCycle<iCount;iCycle++)
    {    
        iArea=iArea+(vecPoly[iCycle].x*vecPoly[(iCycle+1) % iCount].y-vecPoly[(iCycle+1) % iCount].x*vecPoly[iCycle].y);
    }
    
    return abs(0.5*iArea);
}

注意，要注意的是最后一个顶点，要与第一个顶点练成三角形，可将循环变量对顶点总数求同余，则循环过程中的最后一点+1后，自然会成为第一个顶点，上述代码中的“% iCount”即为解决此问题。

C#的实现

      #region CalculateArea Function
        /// <summary>
        /// 计算多边形面积的函数
        /// (以原点为基准点,分割为多个三角形)
        /// 定理：任意多边形的面积可由任意一点与多边形上依次两点连线构成的三角形矢量面积求和得出。矢量面积=三角形两边矢量的叉乘。
        /// </summary>
        /// <param name="vectorPoints"></param>
        /// <returns></returns>
        public static float CalculateArea(List<PointF> vectorPoints)
        {
            int iCycle, iCount;
            iCycle = 0;
            float iArea = 0;
            iCount = vectorPoints.Count;

            for (iCycle = 0; iCycle < iCount; iCycle++)
            {
                iArea = iArea + (vectorPoints[iCycle].X * vectorPoints[(iCycle + 1) % iCount].Y - vectorPoints[(iCycle + 1) % iCount].X * vectorPoints[iCycle].Y);
            }

            return (float)Math.Abs(0.5 * iArea);
        }
        #endregion

参考文章
http://www.cnblogs.com/vbspine/archive/2013/03/28/2987818.html

http://blog.csdn.net/hemmingway/article/details/7814494