Matlab多项式回归实现
多项式回归也称多元非线性回归,是指包含两个以上变量的非线性回归模型。对于多元非线性回归模型求解的传统解决方案,仍然是想办法把它转化成标准的线性形式的多元回归模型来处理。
多元非线性回归分析方程
如果自变数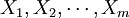 与依变数Y皆具非线性关系,或者有的为非线性有的为线性,则选用多元非线性回归方程是恰当的。例如,二元二次多项式回归方程为:
与依变数Y皆具非线性关系,或者有的为非线性有的为线性,则选用多元非线性回归方程是恰当的。例如,二元二次多项式回归方程为:
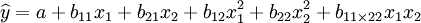
令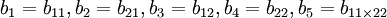 ,及
,及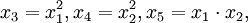 于是上式化为五元一次线性回归方程:
于是上式化为五元一次线性回归方程:
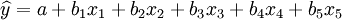
这样以来,便可按多元线性回归分析的方法,计算各偏回归系数,建立二元二次多项式回归方程。
-参考文献:智库百科,点击打开
多元二项式回归Matlab实现方法
1、多元二项式回归Matlab命令
rstool(x,y,'model',alpha)
输入参数说明:
x:n*m矩阵;
Y:n维列向量;
alpha:显著性水平(缺省时为0.05);
mode:由下列4个模型中选择1个(用字符串输入,缺省时为线性模型)
'model'对应的字符串有:'linear'%线性常数和线性项(默认值)
'interaction'%常数、线性和相互作用项
'quadratic'%纯二次拟合函数
'purequadratic'%
2、实例演示说明
设某商品的需求量与消费者的平均收入、商品价格的统计数据如下,建立回归模型,预测平均收入为1000、价格为6时的商品需求量
需求量(y) 100 75 80 70 50 65 90 100 110 60
收入(x1) 1000 600 1200 500 300 400 1300 1100 1300 300
价格(x2) 5 7 6 6 8 7 5 4 3 9
解法一:选择纯二次模型'model'='quadratic'
y=β0+β1x1+β2x2+β11x1^2+β22x2^2
%直接用多元二项式回归如下
x1=[1000 600 1200 500 300 400 1300 1100 1300 300];%1*10矩阵
x2=[5 7 6 6 8 7 5 4 3 9];%1*10矩阵
y=[100 75 80 70 50 65 90 100 110 60]';%1*10矩阵
x=[x1' x2'];%10*2矩阵
rstool(x,y,'purequadratic')
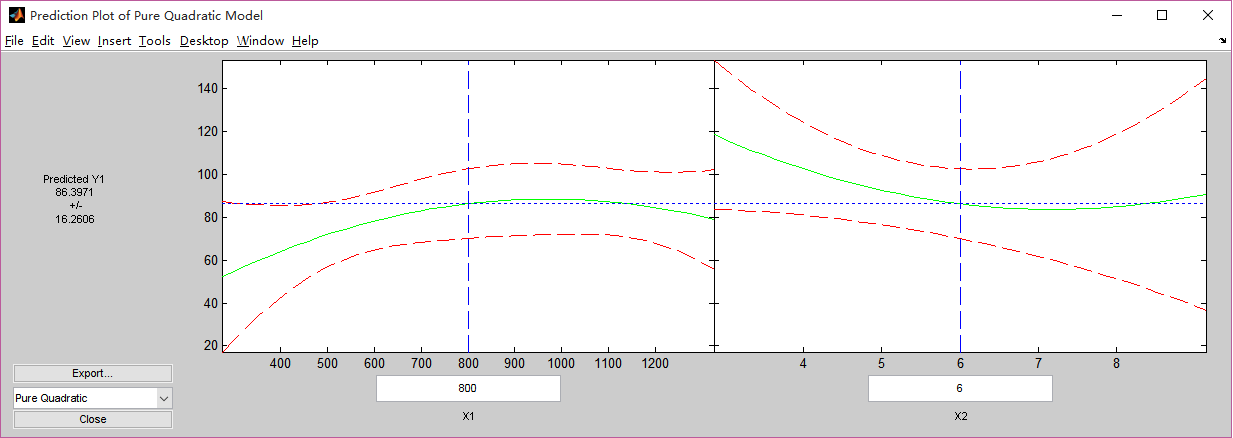
在x1对应的文本框中输入1000,X2中输入6,敲回车键,此时图形和相关数据会自动更新
此时在GUI左边的“Predicted Y1”下方的数据变为88.47981,表示平均收入为1000、价格为6时商品需求量为88.4791
点击左下角的Export按钮,将会导出回归的相关参数beta、rmse和residuals到工作空间(workspace)
在Export按钮下面可以选择回归类型
在Matlab命令窗口中输入
>>beta, rmse
beta =
110.5313%常数项
0.1464
-26.5709
-0.0001
1.8475
rmse =
4.5362%均方根误差
由此得回归模型为:y=110.5351+0.1464x1-26.5709x2-0.0001x1^2+1.8475x2^2
解法二:将上面的模型转换为多元线性回归
y=β0+β1x1+β2x2+β11x1^2+β22x2^2 疑问:为什么没有变量x1*x2呢?官方例子有:地址
>>X=[ones(10,1) x1' x2' (x1.^2)' (x2.^2)'];
>>[b,bint,r,rint,stats]=regress(y,X);
>>b,stats
b =
110.5313
0.1464
-26.5709
-0.0001
1.8475
stats =
0.9702 40.6656 0.0005 20.5771%相关系数R^2、F值、与F值对应的概率(P值)、误差方差估计值



 浙公网安备 33010602011771号
浙公网安备 33010602011771号