ARC117F Gateau 题解

ARC117F Gateau 题解

题解区好像都没有对 dp 详细解释，本文将稍细致地说一说 dp 部分。

题目大意

给定一个长度为 \(2N\) 的环，环上每个节点有属性值 \(B_i\ (i=0,\dots,2N-1)\) 和 \(2N\) 个限制，第 \(i\) 个限制形如 \(\sum\limits_{j=i}^{i+N-1}B_j\geq A_i\)，向环上的节点赋值，使得 \(B\) 满足全部 \(m\) 个限制，且 \(\sum\limits_{i=0}^{2N-1}B_i\) 最小。

Solve

前置芝士：差分约束。

考虑扩环成链，在链尾添加一个等价于 \(0\) 节点的编号为 \(2N\) 的节点，并令 \(S\) 为 \(B\) 的前缀和序列，则限制转化到 \(S\) 上。

设 \(ans=\sum\limits_{i=0}^{2N-1}B_i\)，则：

• \(S_{2N}-S_0=ans\)，即连一条从 \(0\) 到 \(2N\) 的边权为 \(ans\) 的有向边和一条边权为 \(-ans\) 的反向边。

• 对于 \(1\leq i\leq N+1\)，限制转化为：\(S_{i+N-1}-S_{i-1}\geq A_i\iff S_{i-1}-S_{i+N+1}\leq -A_i\)，即连一条从 \(i+N+1\) 到 \(i-1\) 的边权为 \(-A_i\) 的有向边。

• 对于 \(N+1 \leq i \leq 2N\)，限制转化为: \(S_{2N}-S_{i-1}+S_{N-(2N-i+1)=i-N-1}-S_0\geq A_i\iff S_{i-1}\leq S_{i-N-1}+ans-A_i\)，即连一条从 \(i-N-1\) 到 \(i-1\) 的边权为 \(ans-A_i\) 的有向边。（这种情况相当于，把 \(i-1\sim i-N-1\) 都赋值过之后，要给其他地方留至少 \(A_i\)）

• 最后，别忘了对于 \(1\leq i\leq 2N\)，都有 \(S_i\geq S_{i-1}\)，即连一条从 \(i\) 到 \(i-1\) 的边权为 \(0\) 的有向边。

建出的图长这个样子，以 \(N=3\) 为例。

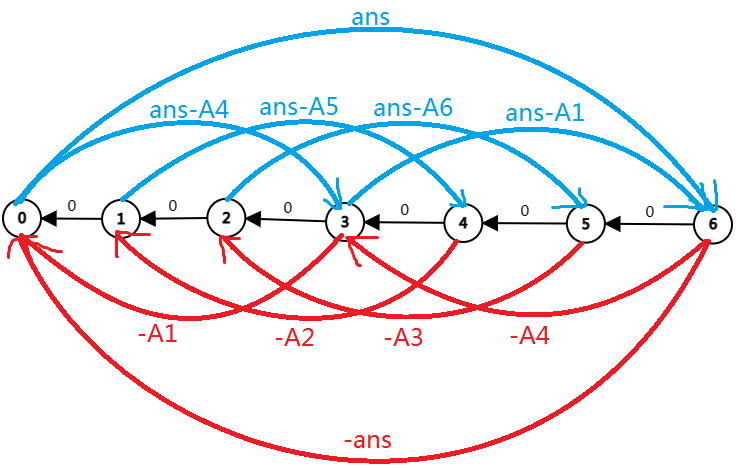
红边为负边权，从右到左，蓝色为正边权，从左到右。

接下来，考虑二分 \(ans\)，若有负环则不合法。

二分下界应取 \(\max\limits_{i=1}^N\{A_i+A_{i+N}\}\)，这样可以免去二元环的考虑。

用 \(\text{SPFA}\) 判负环是 \(O(nm)\) 的，不可行，考虑手动找负环。

负环一定由一些红边和蓝边组成，分两种情况：蓝红蓝（先蓝后红），红蓝红（先红后蓝）。

记以 \(i\) 为起点的蓝边边权为 \(e1_i\)，以 \(i\) 为终点的红边边权为 \(e2_i\)。

• 对于先蓝后红，设 \(f_{i,0/1}\) 表示前 \(i\) 个节点，当前这一步是【（先走红边到前面）从 \(i\) 往右走蓝边 / 前面走蓝边跳到了 \(i\) 右边又走红边走回 \(i\)】的最小环，有转移方程：

\[f_{i,0}=\min\{f_{i-1,0},e1_i,f_{i-1,1}+e1_i\}\\ f_{i,1}=\min\{f_{i-1,1},f_{i-1,0}+e2_i\} \]

• 对于先红后蓝，类似地，设 \(g_{i,0/1}\) 表示前 \(i\) 个节点，当前这一步是【（先走红边到前面）从 \(i\) 往右走蓝边 / 前面走蓝边跳到了 \(i\) 右边又走红边走回 \(i\)】的最小环，有转移方程：

\[g_{i,0}=\min\{f_{i-1,0},f_{i-1,1}+e1_i\}\\ g_{i,1}=\min\{f_{i-1,1},e2_i,f_{i-1,0}+e2_i\} \]

两种情况有什么区别呢？

对于 \(f\)，我们规定在走红边之前必须至少走一条蓝边，所以我们的 \(f_{i,1}\) 不能与 \(e2_i\) 取 \(\min\)，但 \(f_{i,0}\) 可以与 \(e1_i\) 取 \(\min\)，即可以让蓝边与黑边单独成环。

对于 \(g\)，我们规定在走蓝边之前必须至少走一条红边，所以我的们的 \(g_{i,0}\) 不能与 \(e1_i\) 取 \(\min\)，而 \(g_{i,1}\) 可以与 \(e2_i\) 取 \(\min\)，即可以让红边单独成环。

有一个问题：红边怎么单独成环？只需要最后走最上边那条蓝边即可，处理也十分容易，让最后的 \(g_{n,1}\) 加上 \(ans\) 就行了。

全图的最小环即为 \(\min\{f_{n,0}，g_{n,1}+ans\}\)，因为前 \(n\) 个点经过往又跳再跳回来的操作就一定包含了所有情况。

Code

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{
	int x=0;
	short f=1;
	char c=getchar();
	while(c<'0'||c>'9')	{if(x=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')	x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return x*f;
}
const int N=1.5e5+10,M=3e5+10,inf=1e18;
int l,r=inf,n,a[M],m,mid,f[M][2],g[M][2];
int e1[M]/*正边*/,e2[M]/*负边*/;
inline bool chk()
{
	for(int i=0;i<=n;i++)	e1[i]=mid-a[i+n+1];
	f[0][0]=e1[0];f[0][1]=inf;
	g[0][0]=inf;g[0][1]=e2[0];
	for(int i=1;i<=n;i++)
	{
		f[i][0]=min(f[i-1][0],e1[i]);
		f[i][0]=min(f[i][0],f[i-1][1]+e1[i]);
		f[i][1]=min(f[i-1][1],f[i-1][0]+e2[i]);
		g[i][1]=min(g[i-1][1],e2[i]);
		g[i][1]=min(g[i][1],g[i-1][0]+e2[i]);
		g[i][0]=min(g[i-1][0],g[i-1][1]+e1[i]);
	}
	return f[n][0]>=0&&g[n][1]+mid>=0;
}
signed main()
{
	n=read();m=n<<1;
	for(int i=0;i<m;i++)	a[i]=read();
	a[m]=a[0];a[m+1]=a[1];
	for(int i=0;i<=n;i++)	e2[i]=-a[i+1];
	for(int i=1;i<=n;i++)	l=max(l,a[i]+a[i+n]);
	while(l<r)
	{
		mid=l+r>>1;
		if(chk())	r=mid;
		else	l=mid+1;
	}
	return printf("%lld",l),0;
}