ABC359D&E&G 题解

ABC359D Avoid K Palindrome

题目大意

给定一个长度为 \(N\) 的字符串 \(S\)，由 A，B 或 ? 组成。可以在 ? 处任意填 A 或 B。再给定一个常数 \(K\)，问有多少种填法可以使 \(S\) 的每一个长度为 \(K\) 的子串都不是回文串，即成为一个好串。

Solve

注意到 \(K\leq10\)，考虑暴力 \(\text{DFS}\) 或状压 \(\text{DP}\)。由于状态转移比较直观，这里用状压。

令 \(dp_{i,s}\) 表示 \(S\) 的前 \(i\) 位是好串，以 \(i\) 结尾的长度为 \(K\) 的子串状态为 \(s\) 的方案数。\(s\) 二进制下的第 \(j\) 位为 \(1\) 表示 \(S\) 对应的这一位是 A，否则是 B。

对于遍历到的 \(i\)，枚举第 \(i-1\) 位的状态 \(now\)，进行状态转移。

• 若 \(S_i\) 为 A 或 ?，则第 \(i\) 位的状态 \(nxt\) 为 \(now\) 删去最左侧的一位，左移一位，再将对应 \(S_i\) 的最右侧的一位变为 \(1\)，二进制表示为 now<<1&(1<<k)-1|1。
• 若 \(S_i\) 为 B 或 ?，则第 \(i\) 位的状态 \(nxt\) 为 \(now\) 删去最左侧的一位，左移一位，二进制表示为 now<<1&(1<<k)-1。

若 \(nxt\) 不是回文，则令 \(dp_{i,nxt}\) 加上 \(dp_{i-1,now}\)。

Code

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{
	short f=1;
	int x=0;
	char c=getchar();
	while(c<'0'||c>'9')	{if(c=='-')	f=-1;c=getchar();}
	while(c>='0'&&c<='9')	x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return x*f;
}
#define mod 998244353
int n,m,dp[1010][1024]={1},res,ans,k;
char s[1010];
bool f[1024];//预处理出哪些状态不是回文串
signed main()
{
	n=read();m=1<<(k=read());
	scanf("%s",s+1);
	for(int now=0;now<m;now=-~now)
	{
		f[now]=0;
		for(int i=0;i<(k>>1);i=-~i)
			if((now>>i&1)^(now>>(k-1-i)&1))
			{
				f[now]=1;
				break;
			}
	}
	for(int i=1;i<=n;i=-~i)
		for(int now=0;now<m;now=-~now)
		{
			int nxt=now<<1&m-1;
			if(s[i]=='A'||s[i]=='?')
				if(i<k||f[nxt|1])//i<k时特判
					dp[i][nxt|1]=(dp[i][nxt|1]+dp[i-1][now])%mod;//注意取模
			if(s[i]=='B'||s[i]=='?')
				if(i<k||f[nxt])
					dp[i][nxt]=(dp[i][nxt]+dp[i-1][now])%mod;
		}
	for(int now=0;now<m;now=-~now)
		ans=(ans+dp[n][now])%mod;
	return printf("%lld",ans),0;
}

ABC359E Water Tank

题目大意

给定一个长度为 \(N\) 的序列 \(H\)，和一个长度为 \(N+1\) 初始为 \(0\) 的序列 \(A\)。每一轮在 \(A\) 上进行如下操作：

• 将 \(A_0\) 的值增加 \(1\)。
• 依次遍历 \(1\sim N\)，若 \(A_{i-1}>A_i\) 且 \(A_{i-1}>H_i\)，则将 \(A_{i-1}\) 减 \(1\)，将 \(A_i\) 加 \(1\)。

求对于 \(i=1,2,\dots,N\)，需要多少轮操作能使 \(A_i>0\)。

Solve

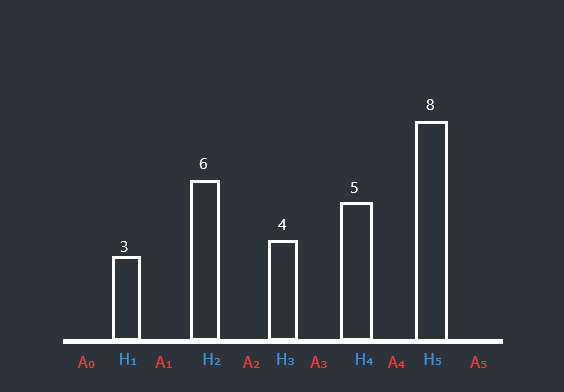
如果要使 \(A_1>0\)，首先要将 \(A_0\) 填满，耗费 \(3\)，再向 \(A_1\) 填 \(1\)。

如果要使 \(A_2>0\)，要将 \(H_2\) 左侧的都填满，共耗费 \(12\)。

如果要使 \(A_5>0\)，要将 \(H_5\) 左侧的都填满，共耗费 \(40\)。

以此类推，若 \(H_i\) 是前缀最大值，那么就要耗费 \(i\times H_i\) 的代价把 \(H_i\) 左侧全填满，也就是填成一个矩形。

那如果 \(H_i\) 不是前缀最大值呢？以 \(H_4\) 为例。

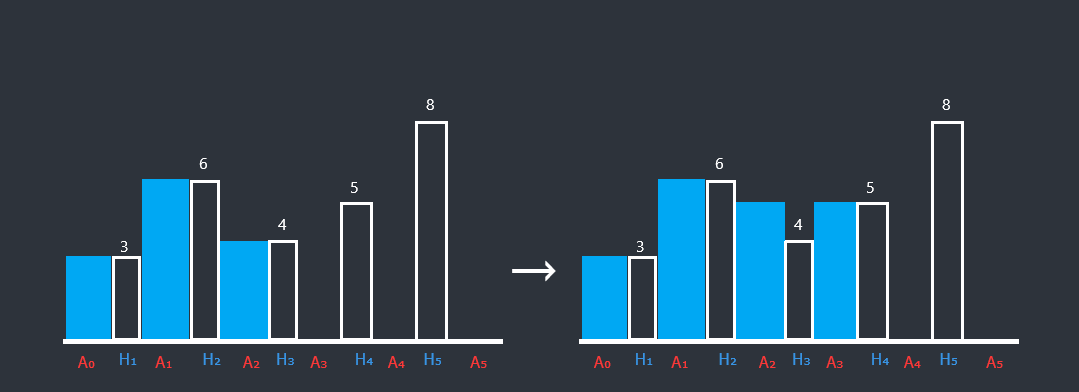
忽略墙的厚度，则相当于把 \(H_2\) 和 \(H_4\) 间填成一个矩形，共耗费 \(H_4\times(4-2)\)。

以此类推，若 \(H_i\) 不是前缀最大值，那么需要去找 \(H_i\) 左侧第一个比它高的 \(H_j\)，花费即为 \(H_i\times(i-j)\)。

单调栈实现之。

Code

// LUOGU_RID: 163040327
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{
	short f=1;
	int x=0;
	char c=getchar();
	while(c<'0'||c>'9')	{if(c=='-')	f=-1;c=getchar();}
	while(c>='0'&&c<='9')	x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return x*f;
}
int n,h[200010],sum[200010];
stack<int>s;
signed main()
{
	n=read();
	for(int i=1;i<=n;i=-~i)
	{
		h[i]=read();
		while(!s.empty()&&h[s.top()]<=h[i])	s.pop();
		if(s.empty())	sum[i]=i*h[i];
		else	sum[i]=sum[s.top()]+(i-s.top())*h[i];
		printf("%lld ",sum[i]+1);
		s.push(i);
	}
	return 0;
}

ABC359G Sum of Tree Distance

题目大意

给定一棵 \(N\) 个节点树，和每个点的权值 \(A_i\)。求 \(\sum\limits_{i=1}^{N-1}\sum\limits_{j=i+1}^Ndis(i,j)\times[A_i=A_j]\)。

Solve

点分治板子啊。

对于分治出的以 \(u\) 为根的子树，令 \(dep[u]\) 为 \(0\)。\(dep\) 是子树中每个点的深度，也就是到根节点的距离。

用 \(sum_i\) 统计所有点权为 \(i\) 的点到子树的根的距离之和，再用 \(cnt_i\) 统计所有点权为 \(i\) 的点的个数，当遍历到点 \(v\) 时，让答案加上 \(sum_{A_v}+cnt_{A_v}\times dep_v\)，也就是加上之前遍历过的点到 \(v\) 点的距离和。然后在遍历完这一分支之后修改 \(sum\) 和 \(cnt\) 数组以实现容斥即可，没啥细节。

Code

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{
	short f=1;
	int x=0;
	char c=getchar();
	while(c<'0'||c>'9')	{if(c=='-')	f=-1;c=getchar();}
	while(c>='0'&&c<='9')	x=(x<<1)+(x<<3)+(c^48),c=getchar();
	return x*f;
}
int n,v[200010],ans;
vector<int>e[200010];
int mn,root,siz[200010];
int dep[200010],sum[200010],now,cnt[200010];
bool vis[200010];
vector<int>a,b;
void get_siz(int u,int fa)
{
	siz[u]=1;
	int mx=0;
	for(auto i:e[u])
		if(i!=fa&&!vis[i])
			get_siz(i,u),
			mx=max(mx,siz[i]),siz[u]+=siz[i];
	mx=max(mx,now-siz[u]);
	if(mx<mn)	mn=mx,root=u;
}
inline int get_rt(int u)/*找重心*/
{
	mn=n;now=siz[u];
	get_siz(u,0);
	return root;
}
void get_dis(int u,int fa)
{
	a.push_back(u);
	for(auto i:e[u])
		if(i!=fa&&!vis[i])
			dep[i]=-~dep[u],
			get_dis(i,u);
}
inline void calc(int u)
{
	dep[u]=1;
	a.clear();
	get_dis(u,0);
	for(auto i:a)
		ans+=sum[v[i]]+dep[i]*cnt[v[i]];
}
void solve(int u)
{
	vis[u]=1;
	cnt[v[u]]=-~cnt[v[u]];/*别忘了算上子树的根*/
	for(auto i:e[u])
		if(!vis[i])
		{
			calc(i);
			for(auto i:a)
				sum[v[i]]+=dep[i],cnt[v[i]]=-~cnt[v[i]],
				b.push_back(i);
		}
	for(auto i:b)	sum[v[i]]-=dep[i],cnt[v[i]]--;
	b.clear();cnt[v[u]]--;
	for(auto i:e[u])
		if(!vis[i])	solve(get_rt(i));
}
signed main()
{
	siz[1]=n=read();
	for(int i=1,a,b;i<n;i=-~i)
		a=read(),b=read(),
		e[a].push_back(b),e[b].push_back(a);
	for(int i=1;i<=n;i=-~i)	v[i]=read();
	solve(get_rt(1));
	return printf("%lld",ans),0;
}

（点分治的写法可能有些丑，凑合着看吧。）