ARC175 A~C 题解
ARC175A Spoon Taking Problem
题目大意
有 \(n\) 个人围成一个环,第 \(i\) 个人左手边是第 \(i\) 个勺子,右手边是第 \(i\%n+1\) 个勺子。每个人的惯用手用一个字符 \(a_i=\) L/R/? 表示,即左手/右手/未知。
给定 \(1\sim n\) 的一个排列 \(P_1,\dots,P_n\) 表示这 \(n\) 个人行动的顺序。第 \(i\) 个人行动时,若他两边的勺子都没被拿走,他将拿走惯用手那边的,否则拿走有勺子那边的。
问存在多少种惯用手组合,使得每个人恰好拿到一个勺子。
Solve
有一个性质:所有人要么都拿左手边,要么都拿右手边的。因为对于相邻的两人,如果左边的选左手,右边的选右手,那么他们之间的勺子就没人拿了,显然是非法的。
接下来考虑什么情况会对答案产生贡献。
当全部选左手时,如果一个人的右边已经被选过,此时不管他的惯用手是什么,他都只能选左手。所以有:
记答案为 \(ans\),初值为 \(1\)。用 \(vis_i\) 表示第 \(i\) 个勺子是否被选过。若 \(a_i=\) ? 且 \(vis_{i\bmod n+1}=1\),则 \(ans=ans\times2\)。
什么情况会无解呢?显然,如果一个人惯用手为右手且到他行动时右手的勺子未被拿走,那么他会选择右手边的,此时不符合全部选左手。即:
若 \(a_i=\) R 且 \(vis_{i\bmod n+1}=0\),则 \(ans=0\)。
全部右手时同理。
Code
#include<bits/stdc++.h>
#pragma GCC optimize(1,2,3,"Ofast","inline")
using namespace std;
#define int long long
#define mod 998244353
inline int read()
{
short f=1;
int x=0;
char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
inline int readc()
{
char c=getchar();
while(c==' '||c=='\n') c=getchar();
return c;
}
int n,p[200010],ans;
char a[200010];
bool vis[200010];
inline int calc(int op/*全部左(0)/右(1)手*/)
{
int sum=1;
for(int i=1;i<=n;i=-~i) vis[i]=0;
vis[p[1]+op]=1;
for(int i=2;i<=n;i=-~i)
{
if((!vis[p[i]%n+1]&&!op&&a[p[i]]=='R')
||(!vis[p[i]]&&op&&a[p[i]]=='L'))
return 0;
if((vis[p[i]%n+1]&&!op&&a[p[i]]=='?')
||(vis[p[i]]&&op&&a[p[i]]=='?'))
sum=(sum<<1)%mod;
if(!op) vis[p[i]]=1;
else vis[p[i]%n+1]=1;
}
return sum;
}
signed main()
{
n=read();
for(int i=1;i<=n;i=-~i) p[i]=read();
for(int i=1;i<=n;i=-~i) a[i]=readc();
if(a[p[1]]=='L'||a[p[1]]=='?') ans+=calc(0);
if(a[p[1]]=='R'||a[p[1]]=='?') ans=(ans+calc(1))%mod;
return printf("%lld",ans),0;
}
ARC175B Parenthesis Arrangement
题目大意
给定一个长度为 \(2n\) 括号序列,对这个括号序列进行若干次以下操作,使得括号匹配。
- 交换序列中的任意两个元素,代价为 \(a\)。
- 修改序列中的任意一个元素,代价为 \(b\)。
Solve
小贪一波。
首先记序列中左括号个数为 \(cnt\),则:
- 若 \(cnt<n\) 即左括号不够,则我们从左端开始填,将前 \(n-cnt\) 个右括号改为左括号是最优的。
- 若 \(cnt>n\) 即右括号不够,则我们从右端开始填,将后 \(cnt-n\) 个左括号改为右括号是最优的。
显然这些操作二是必要的,代价为 \(|n-cnt|\times b\)。
接下来,对于处理出的左右括号数量相等的序列,将 \(a\) 与 \(2b\) 取 \(\min\) 后,执行交换操作一定比执行修改操作要优,这是显然的,因为修改一个元素一定要修改另一个元素使得左右括号数量相等,而这就相当于一次交换操作。
考虑将左括号设为 \(-1\),右括号设为 \(1\)。遍历序列,记录一个前缀和 \(sum\)。若遍历至第 \(i\) 位时 \(sum>0\),则说明需要进行操作,那么考虑贪心:
将这个右括号与最后一个左括号交换一定是最优的。因为交换前后序列的所有括号匹配数一定不会减少且会加 \(1\)。而与任何一个其他位置的左括号交换,括号匹配数有可能减少/不变/加 \(1\)。
Code
// LUOGU_RID: 153163957
#include<bits/stdc++.h>
#pragma GCC optimize(1,2,3,"Ofast","inline")
using namespace std;
#define int long long
inline int read()
{
short f=1;
int x=0;
char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
int n,a,b,cnt,ans,sum=0,res=0;
string s;
signed main()
{
n=read();a=read();b=read();
a=min(a,b<<1);cin>>s;
for(int i=0;i<s.size();i=-~i) if(s[i]=='(') cnt=-~cnt;
if(cnt<n)
for(int i=0,j=0;i<s.size()&&j<n-cnt;i=-~i)
if(s[i]==')') s[i]='(',j=-~j;
if(cnt>n)
for(int i=s.size()-1,j=0;i&&j<cnt-n;i--)
if(s[i]=='(') j=-~j,s[i]=')';
for(int l=0,r=s.size()-1;l<s.size()&&l<r;l=-~l)
{
if(s[l]=='(') sum--;
else sum=-~sum;
if(sum>0)
{
while(s[r]==')'&&r>l) r--;
if(r>l) res=-~res,sum-=2;
}
}
return printf("%lld",abs(n-cnt)*b+res*a),0;
}
ARC175C Jumping Through Intervals
题目大意
给定 \(n\) 个区间 \([l_i,r_i]\)。构造一组 \(A_i\in[l_i,r_i]\),使得邻的 \(A_i\) 的差的和,即 \(\sum\limits_{i=1}^{n-1}|A_i+A_{i+1}|\) 最小。若有多组解,输出字典序最小的一组。
Solve
令 \(f_i(x)\) 表示前 \(i\) 个数,第 \(A_i=x\) 时的最小的相邻两项之差的和。那么 \(f_1(x),x\in[l_1,r_1]=0\)。即 \(f_1(x)\) 的图象是一条在 \(y\) 轴上的线段。
而 \(f_i(x),i\in[2,n]\) 的图象显然是这样的图象的一部分:
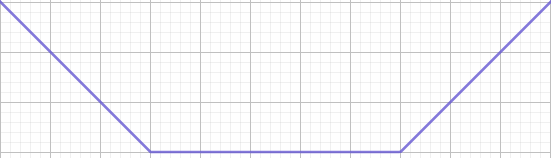
以 \(f_2(x)\) 为例,其图象为:(此时 \([l_1,r_1]=[4,9],[l_2,r_2]=[1,12]\))
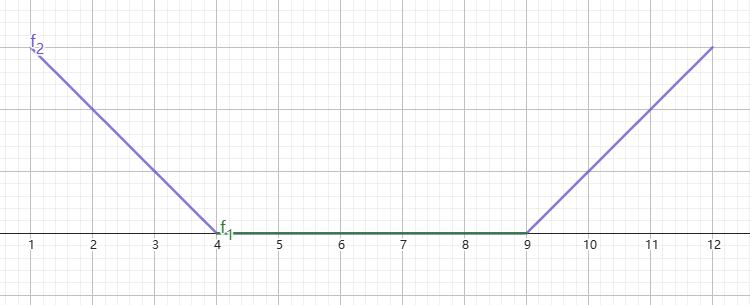
对于 \(x\in[l_2,r_2]\cap[l_1,r_1]=[4,9]\),显然可以直接从 \(f_1(x)\) 上转移过来,代价为 \(0\);否则,从\([l_1,r_1]\) 上最靠近 \(x\) 的点,即 \(l_1\) 或 \(r_1\) 上转移过来最优,代价为 \(l_1-x\) 或 \(x-r_1\)(同无交时)。如果 \([l_2,r_2]\neq[1,12]\),那也不影响图象的总体形状,只是在上边截取一部分或延长一端。
而对于这么个图象,我们只需要记录住它的拐点(即上图中 \((4,0)\) 和 \((9,0)\))就可以知道这个图象长什么样子了。记 \([l_i,r_i]\) 的拐点为 \(a_i\) 和 \(b_i\),则 \([a_i,b_i]\) 上 \(f_i(x)\) 最小,考虑怎么状态转移。
首先,我们有 \([a_1,b_1]=[l_1,r_1]\)。
对于 \(i\in[2,n]\):
- 若 \(r_i<a_{i-1}\),即 \([l_i,r_i]\) 和 \([a_{i-1},b_{i-1}]\) 无交且在其左侧,则此时当且仅当 \(x=r_i\) 时 \(f_i(x)_\min=f_{i-1}(l_{i-1})+l_{i-1}-r_i\),故 \(a_i=b_i=r_i\)。
- 若 \(l_i>b_{i-1}\),即 \([l_i,r_i]\) 和 \([a_{i-1},b_{i-1}]\) 无交且在其右侧,同理有 \(a_i=b_i=l_i\)。
- 否则 \([l_i,r_i]\) 和 \([a_{i-1},b_{i-1}]\) 有交,则对于 \(x\in[l_i,r_i]\cap[a_{i-1},b_{i-1}]\),\(f_i(x)_\min=f_{i-1}(x)\)。故 \([a_i,b_i]=[l_i,r_i]\cap[a_{i-1},b_{i-1}]\),即 \(a_i=\max(l_i,a_{i-1})\),\(b_i=\min(r_i,b_{i-1})\)。
处理完拐点之后,我们来确定这个字典序最小的序列,但这时候就有一个问题:\([a_i,b_i]\) 是由 \([a_{i-1},b_{i-1}]\) 转移来的,但时我们确定字典序是按照从 \(1\) 到 \(n\) 的顺序确定的,这样就会有后效性。所以我们在处理 \([a_i,b_i]\) 时令 \([a_n,b_n]=[l_n,r_n]\),倒着转移即可。
倒着转移完成后,显然 \(A_1=a_1\)。那么在确定 \(A_2\) 的时候,就变成了这样一个问题:
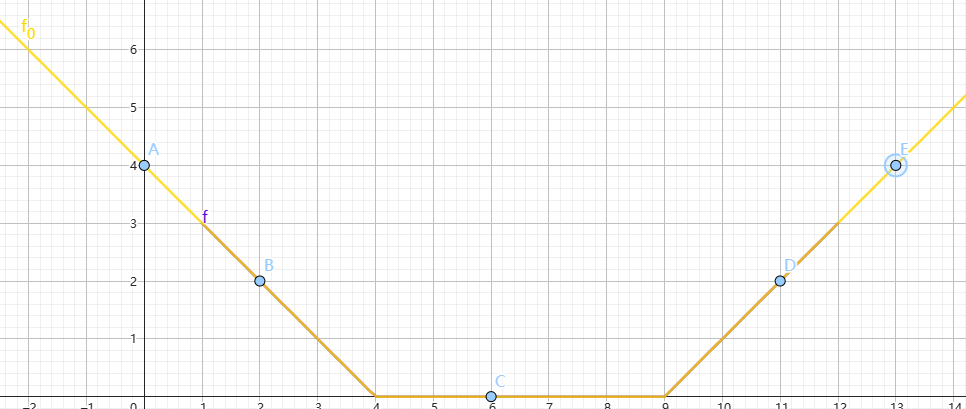
如图,在 \(f_0\) 上给定一点 \(P\in\{A,B,C,D,E\}\),在 \(f_2(x)\) 上找一点 \((x,f_2(x))\),使得 \(g_2(x)=f_2(x)+|x-x_P|\) 最小,若有多个合法的 \(x\),取最小的。
- 若 \(P=A\in{(-\infty,l_2]}\),对于 \(x\in[l_2,a_2]\),\(g_2(x)\) 为定值。因为 \(x\) 每减小 \(1\),\(f_2(x)\) 就增大 \(1\),\(|x-x_A|\) 减小 \(1\),和不变。所以应取 \(x=l_2\)。
- 若 \(P=B\in[l_2,a_2]\),对于 \(x\in[x_B,a_2]\),\(g_2(x)\) 为定值,原因同上。故应取 \(x=x_B\)。
- 若 \(P=C\in[a_2,b_2]\),显然当 \(x=x_C\) 时 \(g_2(x)\) 最小,应取 \(x=x_C\)。
- 若 \(P=D\in[b_2,r_2]\),对于 \(x\in[b_2,x_D]\),\(g_2(x)\) 为定值,原因与第一种情况类似。应取 \(x=b_2\)。
- 若 \(P=E\in[r_2,\infty)\),对于 \(x\in[b_2,r_2]\),\(g_2(x)\) 为定值。应取 \(x=b_2\)。
整理一下并从 \(A_2\) 推广到所有 \(A_i,i\in[2,n]\),有:\(A_i=\begin{cases}l_i&(A_{i-1}<l_i)\\A_{i-1}&(l_i\leq A_{i-1}\leq b_i)\\b_i&(A_{i-1}>b_i)\end{cases}\)。
Code
(代码中 \([a_i,b_i]\) 和 \([l_i,r_i]\) 意义相反。)
// LUOGU_RID: 153163957
#include<bits/stdc++.h>
#pragma GCC optimize(1,2,3,"Ofast","inline")
using namespace std;
#define int long long
inline int read()
{
short f=1;
int x=0;
char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
int a[500010],b[500010],l[500010],r[500010],n,ans[500010];
signed main()
{
n=read();
for(int i=1;i<=n;i=-~i) a[i]=read(),b[i]=read();
l[n]=a[n];r[n]=b[n];
for(int i=n-1;i;i--)
{
if(b[i]<l[-~i]) l[i]=r[i]=b[i];
else if(a[i]>r[-~i]) l[i]=r[i]=a[i];
else l[i]=max(l[-~i],a[i]),r[i]=min(r[-~i],b[i]);
}
printf("%lld ",ans[1]=l[1]);
for(int i=2;i<=n;i=-~i) printf("%lld ",ans[i]=clamp(ans[i-1],a[i],r[i]));
return 0;
}
注:clamp(a,b,c):若 \(a\in[b,c]\) 则返回 \(a\),否则返回 \(b,c\) 中与 \(a\) 的差较小的一个。

 有趣 ,爱写,多出
有趣 ,爱写,多出

 浙公网安备 33010602011771号
浙公网安备 33010602011771号