[数据结构] 排序算法的原理代码及可视化演示

排序算法

本文汇总了核心排序算法及其代码实现：
  - 插入法：直接插入排序，折半插入排序，2-路插入排序（折半插入的改进版）（待更新），希尔排序（待更新）
  - 交换法：冒泡排序，快速排序
  - 选择法：简单选择排序，树形选择排序（待更新），堆排序（待更新）
  - 2-路归并排序
  - 计数排序
  - 桶排序（待更新）
  - 基数排序

1. “插入”

1.1. 直接插入排序

public static void insertSort(int[] nums){
    for(int i = 1;i<nums.length;i++){
        int j = i;
        while(j > 0 && nums[j]<nums[j-1] ){
            int temp = nums[j-1];
            nums[j-1] = nums[j];
            nums[j] = temp;
            j--;
        }
    }
}

1.2. 折半插入排序

public static void binaryInsertSort(int[] nums){
    for(int i=1;i<nums.length;i++){
        int j = i;
        int num = nums[j];
        int left = 0,right = i-1;
        while(left<=right){
            int mid = (left+right)/2;
            if(num >= nums[mid]){
                left = mid + 1;
            }else {
                right = mid - 1;
            }
        }
        for(j=i;j>right+1;j--){
            nums[j]=nums[j-1];
        }
        nums[right+1] = num;
    }
}

2. “交换”

2.1. 冒泡排序

public static void bubbleSort(int[] nums) {
    for(int i = 0;i<nums.length;i++){
        int j=nums.length-1;
        while(j>i){
            if(nums[j]<nums[j-1]){
                int temp = nums[j-1];
                nums[j-1] = nums[j];
                nums[j] = temp;
            }
            j--;
        }
    }
}

2.2. 快速排序

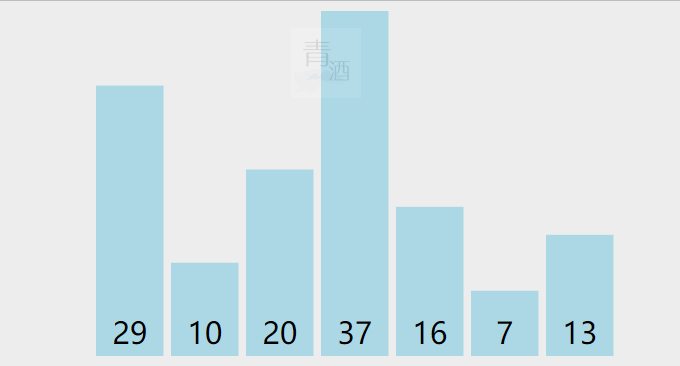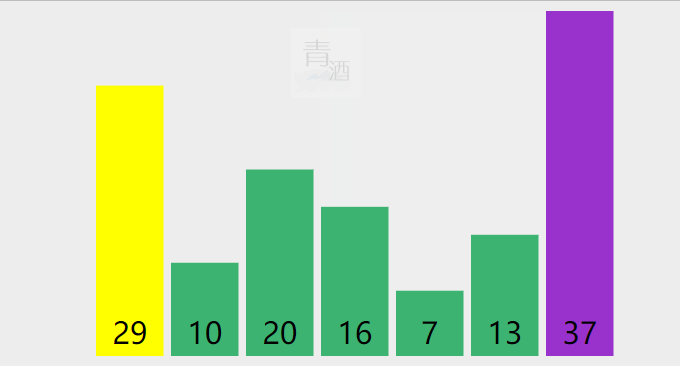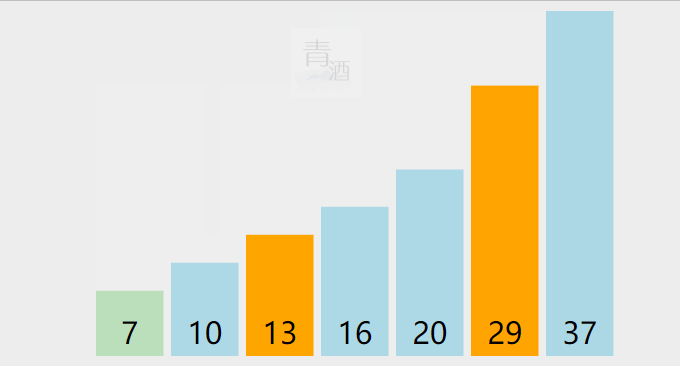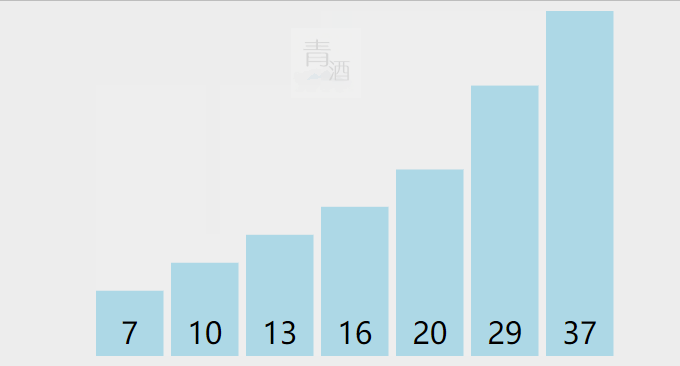
public static void quickSort(int[] nums, int left, int right) {
    if (left < right) {
        int pivot = sort(nums, left, right);
        quickSort(nums, left, pivot - 1);
        quickSort(nums, pivot + 1, right);
    }
}

private static int sort(int[] nums, int left, int right) {
    int point = nums[left];
    int i = left, j = right;
    while (i < j) {
        while (i < j && nums[j] > point) {
            --j;
        }
        if (i < j) {
            nums[i++] = nums[j];
        }
        while (i < j && nums[i] < point) {
            i++;
        }
        if (i < j) {
            nums[j--] = nums[i];
        }
    }
    nums[i] = point;
    return i;
}

3. “选择”

3.1. 简单选择排序

public static void selectSort(int[] nums){
    for(int i=0;i<nums.length;i++){
        int min = nums[i];
        int index = i;
        for(int j=i;j<nums.length;j++){
            if(nums[j]<min){
                min = nums[j];
                index = j;
            }
        }
        int temp = nums[index];
        nums[index] = nums[i];
        nums[i] = temp;
    }
}

3.2. 树形选择排序（待更新）

3.3. 堆排序（待更新）

4. “归并”

4.1. 2-路归并排序

public static void mergeSort(int[] nums,int left,int right){
    int mid = (left+right)/2;
    if(left<right){
        mergeSort(nums,left,mid);
        mergeSort(nums,mid+1,right);
    }
    merge(nums,left,mid,right);
}
private static void merge(int[] nums,int left,int mid,int right){
    if(left<right){
        int[] tempArr = new int[nums.length];
        for(int i=left;i<=right;i++){
            tempArr[i]=nums[i];
        }
        int p=left,q=mid+1,t=left;
        while(p<=mid && q<=right) {
            if (tempArr[p] <= tempArr[q]) {
                nums[t++] = tempArr[p++];
            }else{
                nums[t++] = tempArr[q++];
            }
        }
        while(p<=mid){
            nums[t++]=tempArr[p++];
        }
        while(q<=right){
            nums[t++]=tempArr[q++];
        }
    }
}

5. 计数排序、桶排序、基数排序

5.1. 计数排序

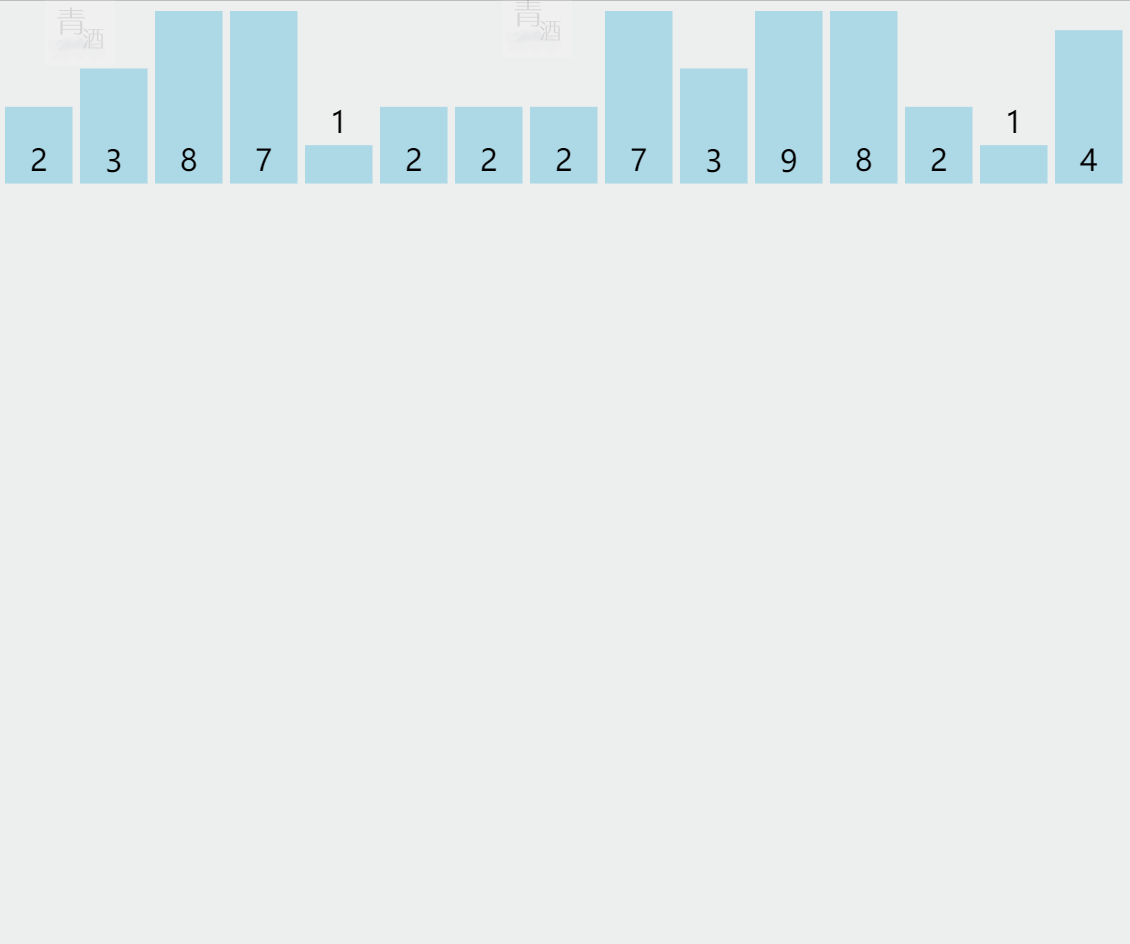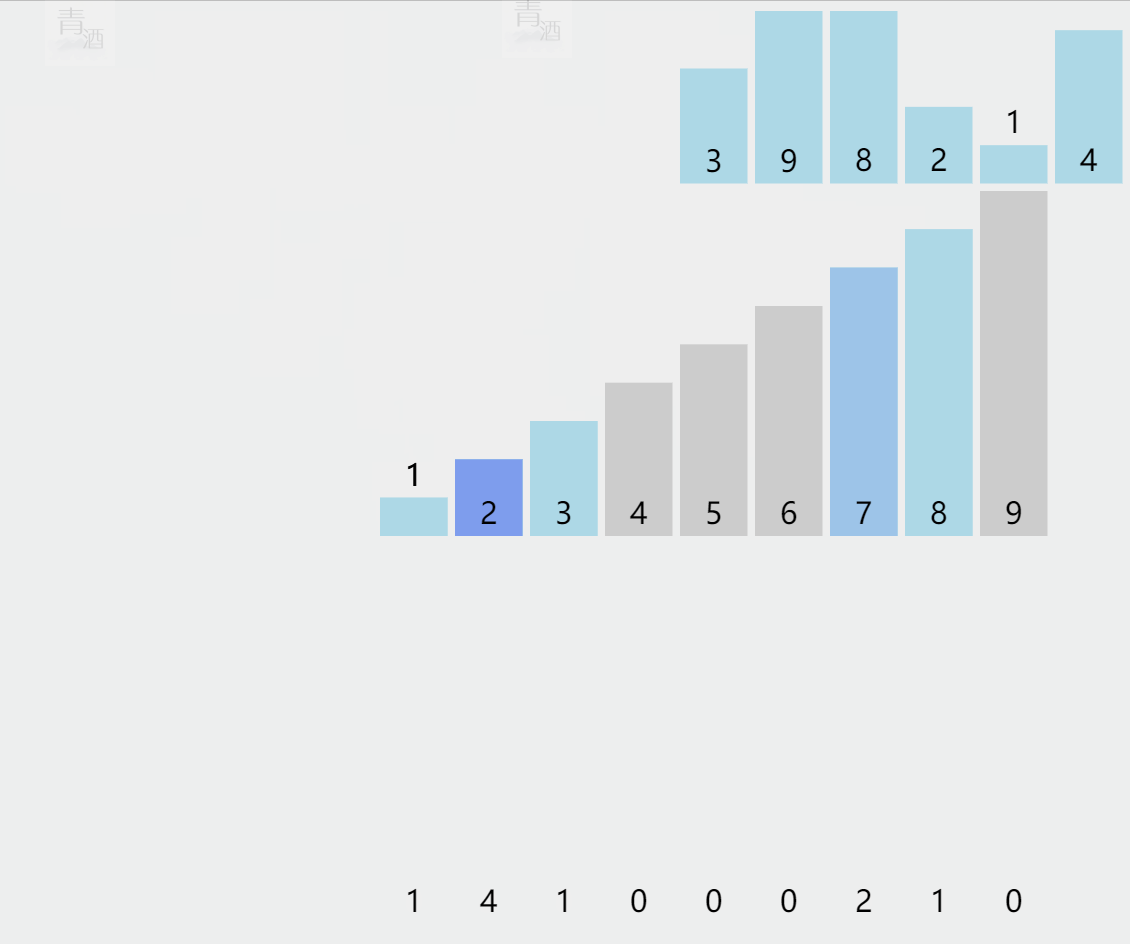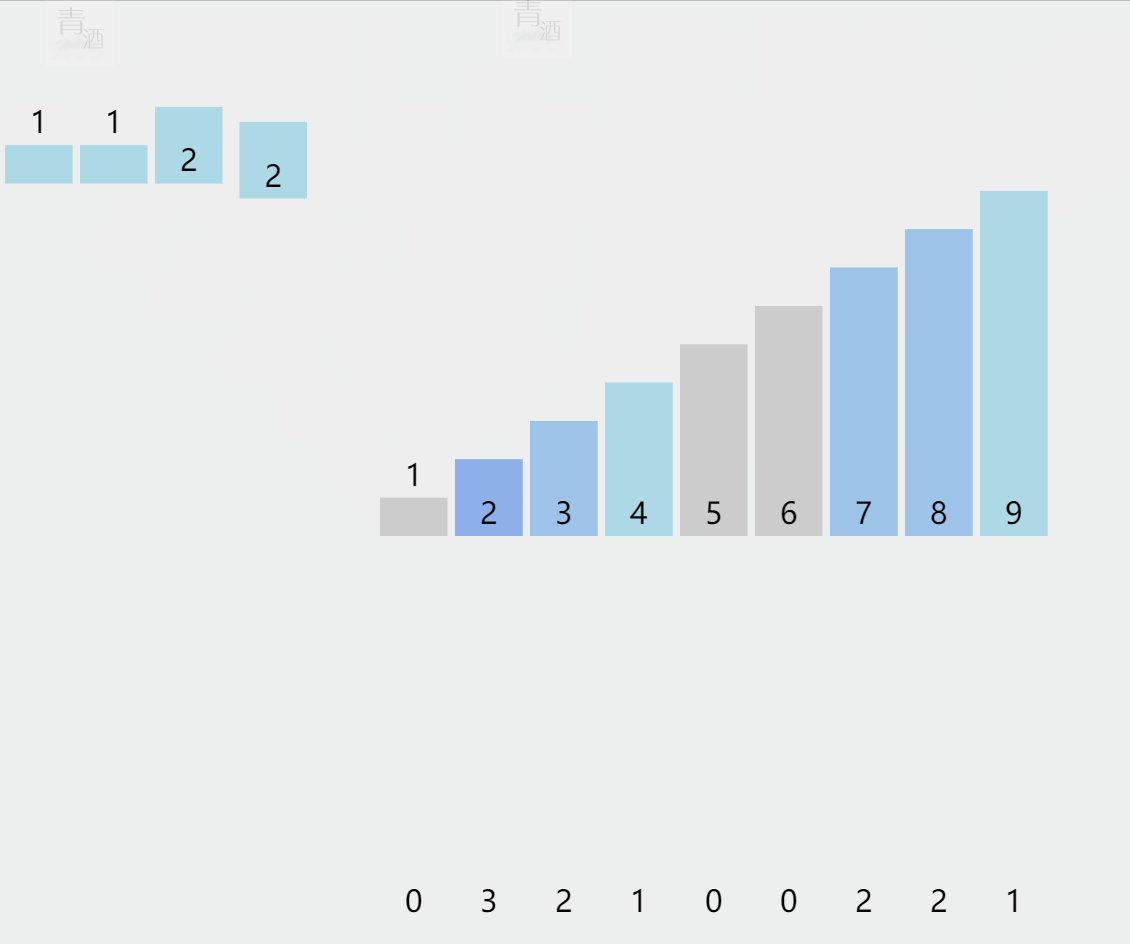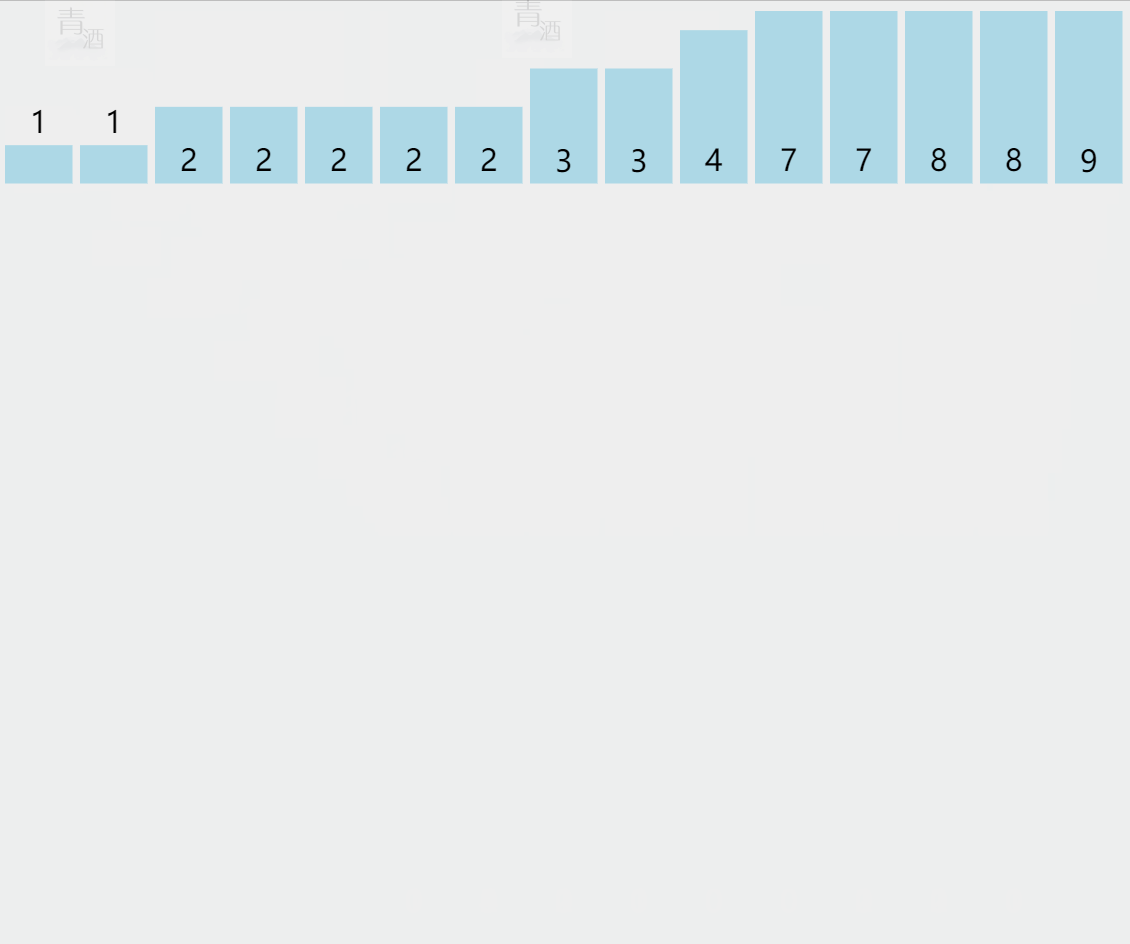
（代码待补充）

5.2. 桶排序（待更新）

5.3. 基数排序

（代码待补充）

---

===后续仍在持续更新===

---

Reference

各排序过程的可视化展示，可访问此网站：Data Structure Visualizations

 

声明：文章图片使用请先获得许可。