图像尺度问题及其描述方法
----------------------------------------------------------------- 尺度不变性 -------------------------------------------------
使得拍摄的物体在任何尺度下都能检测到一致(同一对)关键点.
每个特征点都对应一个尺度因子,一般情况下,不同特征点(同一对)的尺度因子之间的比率应该等于图像尺度的比率
-------------------------------------------------------------- 衡量尺度不变性的方法 -------------------------------------------
必须先要明确这样一个问题:在一幅图像中,只有在一定的尺度范围内,一个物体才有意义。举一个例子,树枝这个概念,只有在几厘米到几米的距离去观察它,才能感知到它的确是树枝;如果在微米级或者千米级去观察,就不能感知到树枝这个概念了,这样的话可以感知到的是细胞或者是森林的概念。因而,如果想要描述现实世界的结构,或者将三维物体映射到二维的图像上去,多尺度表示将会至关重要。这里需要强调一点,事物是实实在在的存在的,但是通过图像这个媒介,观察者可以感知到的概念是不同的,这点很有意思,将实物进行抽象化的转化是图像处理方面很有趣的地方。
1.图像金字塔
图像金字塔是比较老的方法,最开始多用于图像分割,以一些列金字塔形状排列,对同一张图像进行分辨率逐渐降低的操作,它的一个很大的好处是,自下而上每一层的像素数都不断减少,这会大大减少计算量;而缺点是自下而上金字塔的量化变得越来越粗糙,而且速度很快。加上其他的操作常用的金字塔有高斯金字塔和拉普拉斯金字塔,实际中是包含降采样和平滑操作的。
2. 高斯金字塔
因为高斯核是唯一的线性核,也就是说使用高斯核对图像模糊不会引入其他噪声。高斯金字塔是向下采样的,即每次都是降低分辨率(实际上是每次都对图像尺寸减半)。实际中先使用高斯核对图像进行卷积操作(平滑处理),然后删除所有偶数行和偶数列来降低分辨率(这样就变为了原来1/4),因为高斯滤波器是一种低通滤波器(使用低通滤波器的好处还能去除高频噪声),据说高斯核是唯一可以产生多尺度空间的核,那利用小波变换产生的多尺度是咋回事?暂且先搁置下这块。但金字塔中使用了不同尺度的高斯函数进行平滑,所以高斯金字塔仍然可以跨越很大的频率范围.下面是用到的可变高斯函数和与图像做卷积处理的方式

![]()
其中(x,y)是空间坐标,σ是尺度坐标,它的大小决定了图像的平滑程度,不同尺度图像对应不同的σ(σ取值在0.5最清晰-1.6最模糊,论文中取的是1.6),大的σ对应低分辨率图像,小的σ对应高分辨率图像,实时上这跟低分辨率图像因为锯齿更多所以需要更高的平滑程度是相对应的,原则上就是需要任何制度下都是没啥锯齿的图像了。
注:这里将高斯函数进行下详细分析,高斯函数分为一维高斯函数和二维高斯函数,公式如下
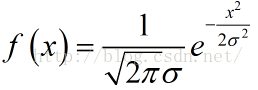
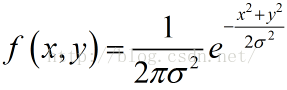
二维高斯模糊具有圆对称性,具有线性可分的性质,即一幅图像进行多次连续高斯模糊的效果和一次更大的高斯模糊效果是相同的,大的高斯模糊的半径是所用多个高斯模糊半径平方和的平方根。例如,使用半径分别为 6 和 8 的两次高斯模糊变换得到的效果等同于一次半径为 10 的高斯模糊效果,另外高斯函数的可分离性是指使用二维矩阵变换得到的效果也可以通过在水平方向进行一维高斯矩阵变换加上竖直方向的一维高斯矩阵变换得到。
3. 高斯差分尺度空间(金字塔)(DOG)
3.1 高斯拉普拉斯算子
首先要说下LOG(laplaci an of gaussian)特征,也成为LOG算子。LOG是目前来说尺度变换最好的,很精确(具体为什么是最好的还没有深刻的认识)。 他是将高斯算子和拉普拉斯算子(梯度的散度)结合的一个算子,Laplace算子在图像中作为边缘检测算子,具有旋转不变性,一个二维图像函数的拉普拉斯变换是各向同性的二阶导数,通过对图像求图像的二阶导数的零交叉点来实现边缘检测,是对图像进行微分操作来实现边缘检测,因此对噪声和离散点比较敏感。公式定义为:
由于拉普拉斯是一种微分算子,它的应用可增强图像中灰度突变的区域,减弱灰度的缓慢变化区域。因此,锐化处理可选择拉普拉斯算子对原图像进行处理,产生描述灰度突变的图像,再将拉普拉斯图像与原始图像叠加而产生锐化图像,这种简单的锐化方法既可以产生拉普拉斯锐化处理的效果,同时又能保留背景信息。更为详细的有关拉普拉斯算子的资料可以参照网址 https://blog.csdn.net/li_wen01/article/details/72864291 。因为Laplace算子的性质使得对噪声和离散点也具有增强的效果(对这些比较敏感),所以需要事先通过高斯滤波进行降噪处理,这便是LOG算子。
利用高斯核要继续建立高斯拉普拉斯金字塔,高斯金字塔一般选取4 阶(阶或组用Octave表示)每一阶有5 层(层用Interval表示)的结构。首先对两幅图像进行归一化处理以使得两幅图像的的平均灰度值相等,之后将图像的分辨率扩大到原来的两倍再对其进行尺度因子为σ的高斯模糊,令处理得到的图像作为高斯金字塔第一阶的第一层,这里取图像的2 倍是为了得到更多的特征点。
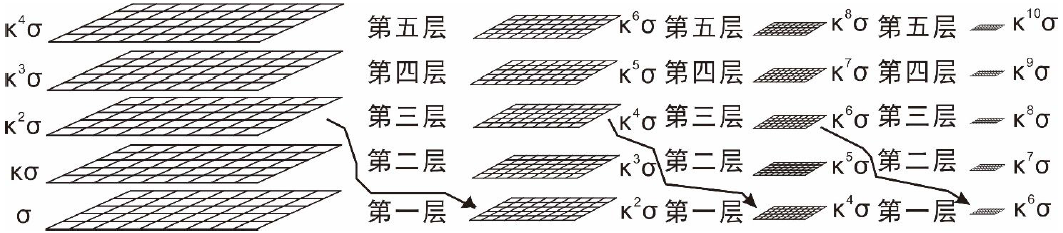
同一阶相邻两层的尺度因子比例是k,则第一阶的第二层的尺度因子是kσ(这里k如何取值还没有弄清楚),以此类推得到第一阶的各层的尺度因子。第2 阶的第一层是由第1 阶的中间层即第3 层进行子抽样得到的(因为与拉普拉斯金字塔不同,高斯金字塔是一种下采样的金字塔,所以采样的方法是下层图像先用高斯核进行卷积运算,之后从图像中删掉偶数行和偶数列就得到上层待运算的图像),其尺度因子也是k2σ,同样第3 阶的第一层是由第2 阶的中间层子采样得到的,这样循环操作得到高斯金字塔。高斯金字塔包含了一些列的低通滤波器,每两层之间的截止频率是以因子2 为间隔的,所以高斯金字塔可以涵盖很大的频率范围。
这样(o(Octave),s(Interval))就能够确定高斯金字塔中的唯一一幅图像了,这是个三维空间,两维坐标,一维是图像。根据lowe的论文,(o,s)作用于一幅图像是通过公式,其中s表示第几层,S表示总共的层数。
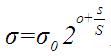
通过公式也可以看出,尺度空间是连续的,两个变量控制着δ的值,其中在第一个八度中有 1<(o+s/S)<=2 ,同理在第二个八度中有2<(o+s/S)<=3,以此类推,δ中的关键部分(o+s/S)部分是逐渐增大的(具体实现时,有些高斯金字塔中这个值是增大,但不是逐渐均匀增大,只能说是连续的)。
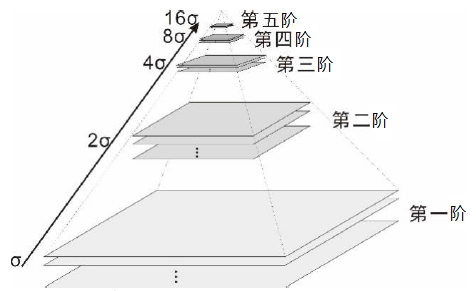
另一种说法是对于上面的高斯金字塔图中第一阶中的图像的尺度分别是δ,kδ,k^2δ......,第二阶尺度分别是2δ,2kδ,2k^2δ........,同理第三阶的尺度分别是4δ,4kδ,4k^2δ........。这个序列是通过下式来确定的(这种说法的解释是最完整的):
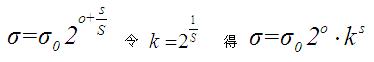
所以每增加一阶,δ都要扩大2倍,在一阶内,k的上标s来区分不同的高斯核。
3.2 用DOG近似替代LOG
LOG计算比较费劲(为什么这么说还不是很清楚),所以用DOG来近似替代,DOG和LOG只差了一个常数,所以保持了最大值和最小值的不变。
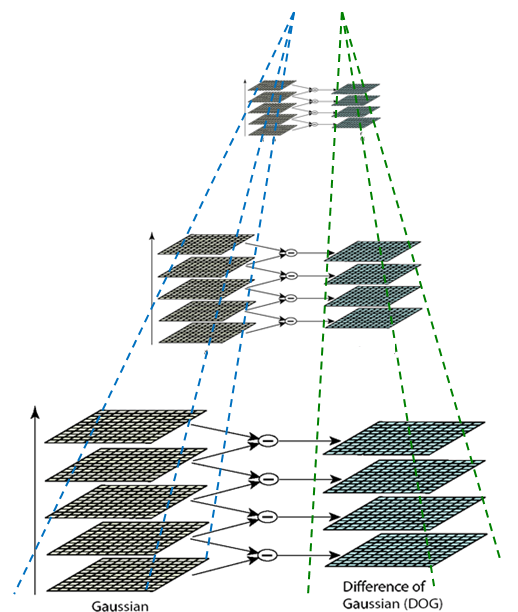
为了有效的在尺度空间检测到稳定的关键点(这点至今也不是很理解稳定的关键点具体是什么),提出了高斯差分尺度空间(DOG scale-space),利用不同尺度的高斯差分核与图像卷积生成,处理方式如下

示意图如下
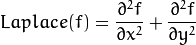


 浙公网安备 33010602011771号
浙公网安备 33010602011771号