十六届蓝桥杯省赛C++A组A-F
题目文件链接 解压密码 65Tg7d9d
题解仅供参考,黑客那道在洛谷T一个点
A: 寻找质数
本题总分:5分
【问题描述】 如果一个正整数只能被1和它本身两个数整除,就称为一个质数。最小的 几个质数依次是2,3,5,7,11,13,··· 请问,第2025 个质数是多少?
【答案提交】 这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个 整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路
筛质数,从小到大就行了,一般来说小于等于 n 的质数个数为 n/ln(n) , (acwing上听的,查了一下是素数定理)最后的数不会太大
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
int primes[2030];
signed main()
{
int cnt = 0;
for(int i = 2; ; i ++)
{
bool flag = true;
for(int j = 0; j < cnt; j ++)
if(i % primes[j] == 0)
{
flag = false;
break;
}
if(flag)primes[cnt ++] = i;
if(cnt == 2025)break;
}
cout<<primes[2024]<<endl; //17609
return 0;
}
B: 黑白棋
本题总分:5分
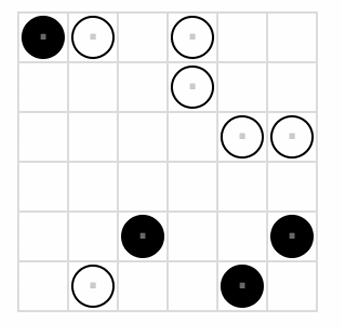
【问题描述】 小蓝最近迷上了一款名为“黑白棋填充”的游戏。该游戏在一个方形网格棋 盘上进行,其中部分格子已经填有黑色或白色的棋子,而其他格子为空,等待 玩家填入棋子。 游戏规则是,玩家需要按照以下规则填满整个棋盘,才能算作胜利:
- 黑白棋子数量均等: 在每一行和每一列中,黑色棋子和白色棋子的数量必须相等。
- 相邻棋子限制: 在棋盘的任何一行或一列中,不能有超过两个相同颜色的棋子连续排列 (即不允许出现“黑黑黑”’或“白白白”的情况)。
- 行列唯一性: 每一行的棋子排列方式必须是唯一的,不能与棋盘中的任何其他行完全相 同。 每一列的棋子排列方式必须是唯一的,不能与棋盘中的任何其他列完全相 同。 行与列之间的棋子排列不作比较,即行可以与列相同,无需满足行列间的 唯一性。

思路
已经填好了一些棋子,然后要让最后的符合规则,本来用的dfs 一行完成check一下,一列完成check一下,然后跑了好长时间没跑出来,耗了半小时没耗出来然后去做后面了,后面该做的做完又回来看了一下,干脆直接枚举完再check一下,不容易出错,然后就出了。。。
前两道题还是得写得越简单越清晰越好
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 10;
int g[N][N];
#define int long long
bool arr(vector<int> &v)
{
for(int i = 0; i + 2 < 6; i ++)
if(v[i] == v[i + 1] && v[i + 1] == v[i + 2])return false;
int cnt = 0;
for(int i = 0; i < 6; i ++)
if(v[i] == 1)cnt ++;
if(cnt != 3)return false;
return true;
}
bool check(int state)
{
memset(g, 0, sizeof g);
g[1][1] = g[5][3] = g[5][6] = g[6][5] = 1;
g[1][2] = g[1][4] = g[2][4] = g[3][5] = g[3][6] = g[6][2] = 2;
int cnt = 0;
for(int i = 1; i <= 6; i ++)
for(int j = 1; j <= 6; j ++)
if(!g[i][j])
{
g[i][j] = (state >> cnt & 1) ? 1 : 2;
cnt ++;
}
map<vector<int>, bool> r, c;
for(int i = 1; i <= 6; i ++) //r
{
vector<int> v;
for(int j = 1; j <= 6; j ++)
v.push_back(g[i][j]);
if(!arr(v))return false;
if(r[v])return false;
r[v] = true;
}
for(int j = 1; j <= 6; j ++)
{
vector<int> v;
for(int i = 1; i <= 6; i ++)
v.push_back(g[i][j]);
if(!arr(v))return false;
if(c[v])return false;
c[v] = true;
}
return true;
}
signed main()
{
g[1][1] = g[5][3] = g[5][6] = g[6][5] = 1;
g[1][2] = g[1][4] = g[2][4] = g[3][5] = g[3][6] = g[6][2] = 2;
for(int i = 0; i < 1 << 26; i ++)
if(check(i))break;
for(int i = 1; i <= 6; i ++)
{
for(int j = 1; j <= 6; j ++)
{
cout<<abs(g[i][j] - 2);
}
cout<<endl;
}
return 0;
}
/*
101001
010011
101100
010110
011001
100110
101001010011101100010110011001100110
*/
C: 抽奖
时间限制: 1.0s 内存限制: 256.0MB 本题总分:10分




思路
模拟题, 把编号 -1,每次转的时候加一下模一下n就行了
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int a[N], b[N], c[N];
int check(int x, int y, int z)
{
if(a[x] == b[y] && a[x] == c[z])return 200;
else if(a[x] == b[y] || a[x] == c[z] || b[y] == c[z])return 100;
else if(a[x] == b[y] - 1 && b[y] + 1 == c[z])return 200;
else
{
vector<int> v = {a[x], b[y], c[z]};
sort(v.begin(), v.end());
if(v[0] + 1 == v[1] && v[1] + 1 == v[2])return 100;
}
return 0;
}
int main()
{
int n;cin>>n;
for(int i = 0; i < n; i ++)cin>>a[i];
for(int j = 0; j < n; j ++)cin>>b[j];
for(int i = 0; i < n; i ++)cin>>c[i];
int m;cin>>m;
int id1 = 0, id2 = 0, id3 = 0;
long long ans = 0;
while(m --)
{
int a1, b1, c1;
cin>>a1>>b1>>c1;
id1 = (id1 + a1) % n, id2 = (id2 + b1) % n, id3 = (id3 + c1) % n;
ans += check(id1, id2, id3);
}
cout<<ans<<endl;
return 0;
}
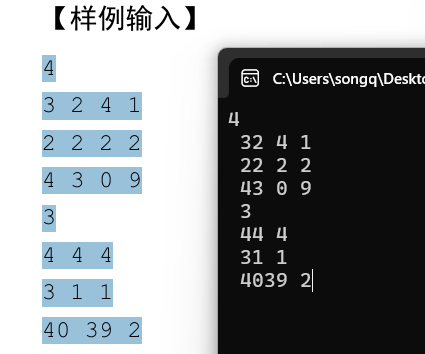
/*
4
3 2 4 1
2 2 2 2
4 3 0 9
3
4 4 4
3 1 1
40 39 2
*/
D: 红黑树
时间限制: 1.0s 内存限制: 256.0MB 本题总分:10分
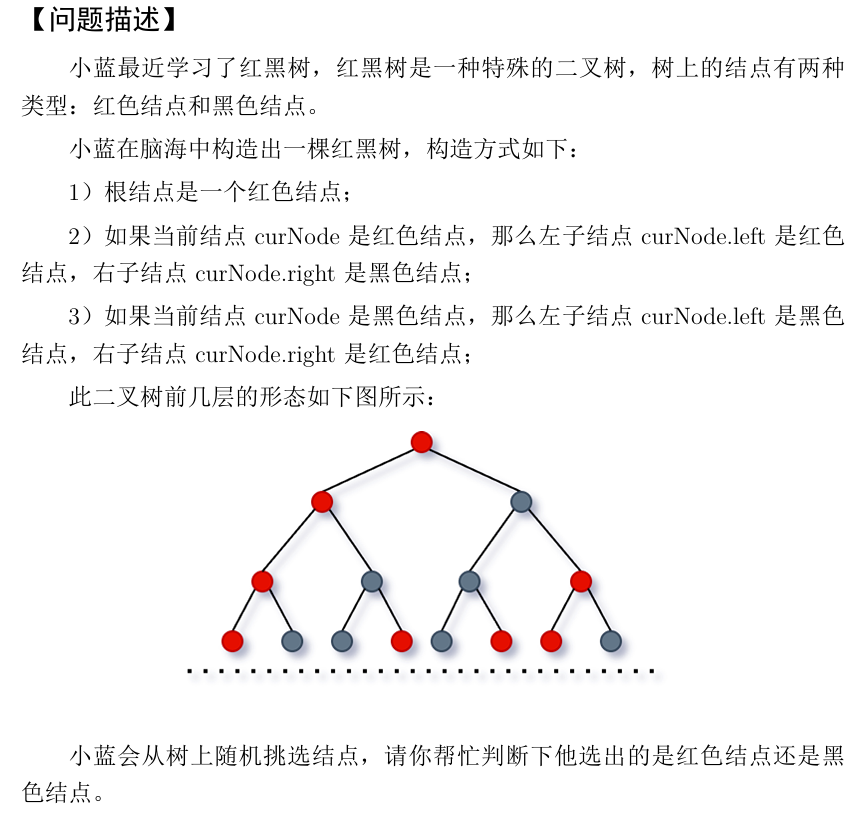



思路
看题目是没学过的数据结构,不做了
一个根节点左边变右边不变,那么我们只要知道所求点的编号判断经过了几次右子树就行了,奇数次就黑,偶数次就红
编号等于当前层第几个 + 上边所有层 = k + 2^(n - 1) - 1
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
bool check(vector<int> v)
{
bool st = true;
for(int i = v.size() - 2; i >= 0; i --)
if(v[i]) //右树
st = !st;
return st;
}
signed main()
{
int m;cin>>m;
while(m --)
{
int n, k;
vector<int> v;
cin>>n>>k;
k += (1LL << (n - 1)) - 1;
while(k)
{
v.push_back(k&1);
k/=2;
}
if(check(v))cout<<"RED"<<endl;
else cout<<"BLACK"<<endl;
}
}
E: 黑客
时间限制: 1.0s 内存限制: 256.0MB 本题总分:15分



思路
先找矩阵的两维长度,存下可能的(n, m),然后看元素里有没有,注意这里要分n=m和n!=m
然后思考对于一个矩阵所有元素排列应该是怎么样的,只要是一个位置不一样就是一种不同的结果,那么n行m列元素完全可以排成一排,求所有元素全排列有多少种不同结果。
然后就是高中知识,对于一个相同的元素(k个)的排列重复结果是k!, 要求的结果就是(nm)! / (ki)!
对于阶乘,由于数据过大,要用到逆元知识,i的逆元= qmi(i, mod - 2); 逆元用快速幂求即可
PS:去洛谷测了一下,只过了40%,然后发现数组开成1e5了wuwuwu~,增大之后发现还是有一个点TLE了
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mod = 1000000007;
const int N = 500010;
int fact[N], infact[N];
int qmi(int a, int b)
{
int res = 1;
while(b)
{
if(b & 1)res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
int cul(int n, map<int, int> &mp)
{
vector<int> v;
for(auto i: mp)
if(i.second)v.push_back(i.second);
int res = fact[n];
for(auto i : v)res = res * infact[i] % mod;
return res;
}
signed main()
{
int n;cin>>n;
map<int, int> mp; //记录元素
for(int i = 1; i <= n; i ++)
{
int x;cin>>x;
mp[x] ++;
}
vector<pair<int, int>>v;
n -= 2;
for(int i = 1; i <= n / i; i ++) //统计n,m 的可能值
if(n % i == 0)v.push_back({i, n / i});
int ans = 0;
fact[0] = infact[0] = 1;
for(int i = 1; i < N; i ++) // 存下阶乘与逆元
{
fact[i] = fact[i - 1] * i % mod;
infact[i] = infact[i - 1] * qmi(i, mod - 2) % mod;
}
for(auto i : v)
{
int a = i.first, b = i.second;
map<int, int> tmp = mp;
if(a == b) //相等情况
{
if(tmp[a] >= 2)
{
tmp[a] -= 2;
ans = (ans + cul(n, tmp) ) % mod;
}
}
else
{
if(tmp[a] && tmp[b])
{
tmp[a] --, tmp[b] --;
ans = (ans + cul(n, tmp) * 2 )% mod; // 由于(n, m), (m, n)个数相同直接*2即可
}
}
}
cout<<ans<<endl;
return 0;
}
/*
6
2 2 1 4 3 3
*/
F: 好串的数目
时间限制: 1.0s 内存限制: 256.0MB 本题总分:15分




思路
当时没细想,想着做后面的题,直接暴力5分钟解决了,然后后面两题不会写,就老实回来把这道题优化了
贴一下暴力时期珍贵代码照片


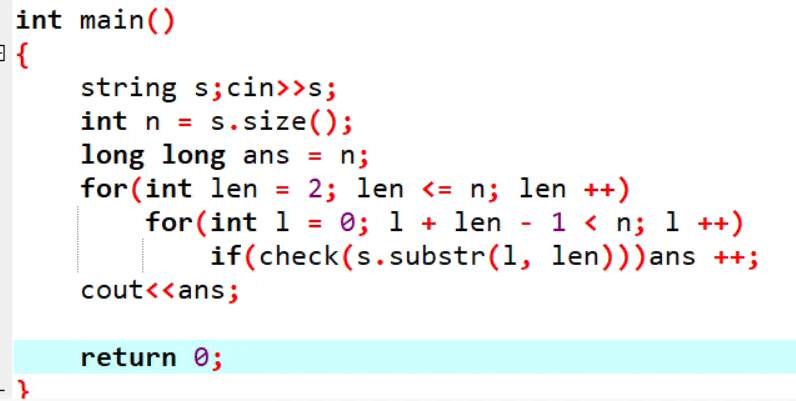
优化思路就是找到连续的片段,记录下这些片段长度,然后片段内好串个数就是1-长度的等差数列求和,片段外好串只有两个相邻片段会有,个数为相邻片段长度相乘
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
signed main()
{
string s;cin>>s;
int n = s.size();
vector<int> v;
v.push_back(0);
for(int i = 1; i < n; i ++)
if(!(s[i] == s[i - 1] || s[i] == s[i - 1] + 1))v.push_back(i);
v.push_back(n);
vector<int> v2;
for(int i = 1; i < v.size(); i ++)
v2.push_back(v[i] - v[i - 1]);
int num[100010];
for(int i = 1; i <= n; i ++)num[i] = i + num[i - 1];
int ans =0;
for(int i = 0; i < v2.size(); i ++)
{
ans += num[v2[i]];
if(i)ans += v2[i] * v2[i - 1];
}
cout<<ans;
return 0;
}
最后两题就真一点不会,然后去优化前面的题去了,慢慢悠悠到后面发现没时间了,幸好手速过快,并且过于大胆,最后的时候优化完过了一个样例就交了,另一个样例还是结束完测的要是没过就紫砂了。
不过想吐槽一下这代码界面没法ctrlA全选删除,还得自己用鼠标划着删,还有pdf复制样例没法直接粘到控制台,会漏空格


 浙公网安备 33010602011771号
浙公网安备 33010602011771号