- modeling(建模)
- Viewing(可视化)
为什么translation?
1. 建模:转化
![]()
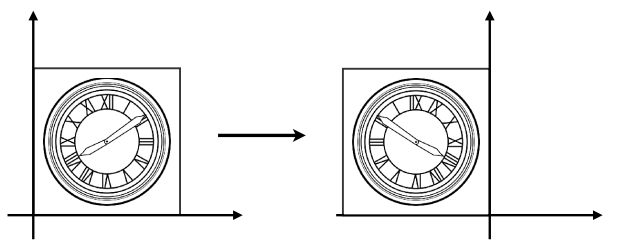
2. 建模:旋转
![]()
3. 建模:变换尺度
![]()
这个是Pixar公司的开场动画,那个小人一直在踩字母‘I’,这个插入gif有点问题,就用截图了。
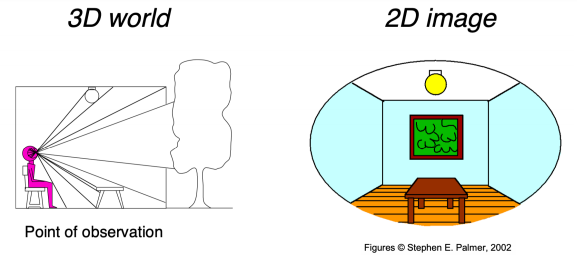
4. 3D到2D的投影
![]()
( 一 )缩放变换(Scale)
1. 均匀缩放:
![]()
上图表示横纵轴均缩放0.5,数学表达:
\[x' = sx \\
y' = sy
\]
矩阵表达方式:
\[\left[
\begin{matrix}
x' \\
y'
\end{matrix}
\right]
= \left[
\begin{matrix}
s & 0 \\
0 & s \\
\end{matrix}
\right]
\left[
\begin{matrix}
x \\
y
\end{matrix}
\right]
\]
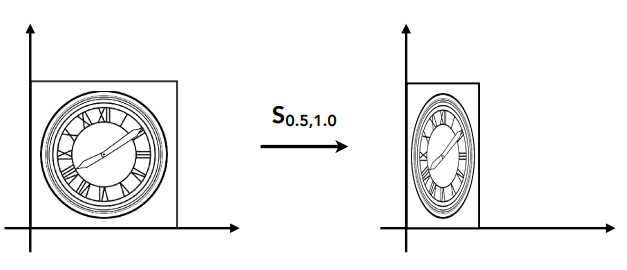
2. 不均匀缩放:
比如下图,水平方向缩小一半,竖直方向不变。
![]()
矩阵表示:
\[\left[
\begin{matrix}
x' \\
y'
\end{matrix}
\right]
=
\left[
\begin{matrix}
s_x & 0 \\
0 & s_y
\end{matrix}
\right]
\left[
\begin{matrix}
x \\
y
\end{matrix}
\right]
\]
( 二 )反射矩阵(Reflection Matrix)
![]()
水平反射矩阵:
\[\left[
\begin{matrix}
x' \\
y'
\end{matrix}
\right]
= \left[
\begin{matrix}
-1 & 0\\
0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x \\
y
\end{matrix}
\right]
= \left[
\begin{matrix}
-x \\
y
\end{matrix}
\right]
\]
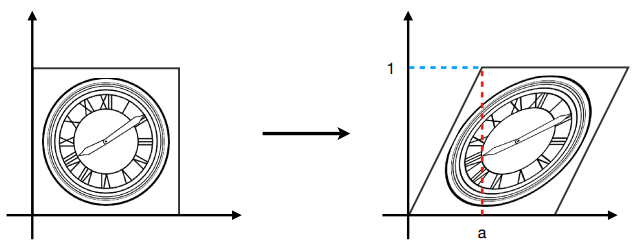
( 三 )切变矩阵(Shear Matrix)
提示:
水平位移在y = 0 时为0
水平位移在y = 1时为a
垂直位移始终为0。
![]()
切变矩阵表达式:
\[\left[
\begin{matrix}
x' \\
y'
\end{matrix}
\right]
=\left[
\begin{matrix}
1 & a \\
0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x \\
y
\end{matrix}
\right]
\]
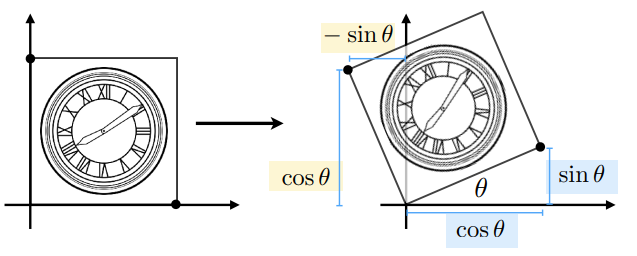
( 四 )旋转(关于原点\((0,0),默认逆时针方向(counterclockwise,CCK)\))
![]()
计算旋转矩阵的手推公式:
![]()
计算出来的旋转公式:
\[R_{\theta} =
\left[
\begin{matrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{matrix}
\right]
\]
线性变换 = 矩阵(相同维度)
![]()
三、齐次坐标(Homogeneous coordinates)
( 一 )为什么使用齐次坐标?
![]()
因为对于平移(Translation),很难写出相同维度的矩阵,只能写成如下形式:
\[\left[
\begin{matrix}
x' \\
y'
\end{matrix}
\right]
= \left[
\begin{matrix}
a & b \\
c & d
\end{matrix}
\right]
\left[
\begin{matrix}
x \\
y
\end{matrix}
\right]
+ \left[
\begin{matrix}
t_x \\
t_y
\end{matrix}
\right]
\]
注:平移不是线性变换。
鉴于平移的特殊性,为了统一变换的矩阵书写模式,因此我们引入了“齐次坐标( Homogenous Coordinates)”
( 二 )添加第三个坐标( W 坐标)
1. 2D point = \((x,y,1)^T\)
2. 2D vector = \((x,y,0)^T\)
3. 用矩阵表示平移:
\[\begin{pmatrix}
x' \\
y' \\
w'
\end{pmatrix} =
\begin{pmatrix}
1 & 0 & t_x \\
0 & 1 & t_y \\
0 & 0 & 1
\end{pmatrix}
\cdot
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
= \begin{pmatrix}
x + t_x \\
y + t_y \\
1
\end{pmatrix}
\]
向量具有平移不变性。
( 三 )齐次变换
- 关于 w 坐标的值是1或者0,是有含义的
(1) 加减运算:
- vector + vector = vector
- point – point = vector
- point + vector = point (一个点沿着一个向量移动,得到一个新的点。)
- point + point = ??
(2)关于point + point的扩充定义:
\(\begin{pmatrix}
x \\
y\\
w
\end{pmatrix}\)是一个2D point\(\begin{pmatrix} x/w \\ y/w \\ 1 \end{pmatrix},w \not= 0\)
仿射变换,又称仿射映射,是指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。
1. Affine map = linear map + translation
\[\begin{pmatrix}
x' \\
y'
\end{pmatrix}
= \begin{pmatrix}
a & b\\
c & d
\end{pmatrix}
\cdot \begin{pmatrix}
x \\
y
\end{pmatrix}
+ \begin{pmatrix}
t_x \\
t_y
\end{pmatrix}
\]
2. 使用齐次坐标
\[\begin{pmatrix}
x' \\
y'\\
1
\end{pmatrix}
= \begin{pmatrix}
a & b & t_x \\
c & d & t_y \\
0 & 0 & 1
\end{pmatrix}
\cdot
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
\]
仿射变换下的齐次坐标,最后一行永远为(0,0,1),其余的变换最后一行还有其他意义,后续课程会详细讲解。由此得出第3点:2D变换。
使用齐次坐标优缺点
- 优点:可以统一表示仿射变换,且最后一行为(0,0,1)
- 缺点:多一行,存储空间占用更大。
3. 2D 变换
(1)缩放
\[S(s_x,s_y) =
\begin{pmatrix}
s_x & 0 & 0 \\
0 & s_y & 0 \\
0 & 0 & 1
\end{pmatrix}
\]
(2)旋转
\[R(\alpha) =
\begin{pmatrix}
\cos \alpha & -\sin \alpha & 0 \\
\sin \alpha & \cos \alpha & 0
0 & 0 & 1
\end{pmatrix}
\]
(3)平移
\[T(t_x,t_y) =
\begin{pmatrix}
1 & 0 & t_x \\
0 & 1 & t_y \\
0 & 0 & 1
\end{pmatrix}
\]
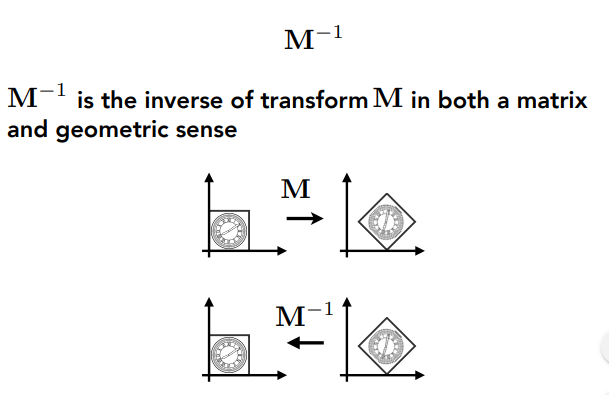
( 四 )逆变换
示意图:
![]()
\(M^{-1}\)将变换后的图像变换为原图像(类似:逆矩阵)。
( 五 )组合变换
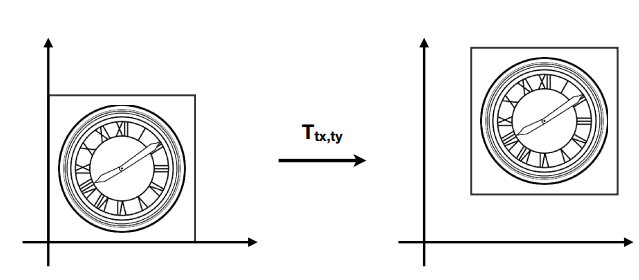
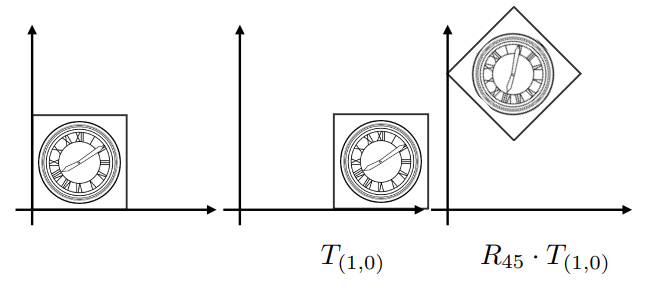
举例1:先平移后旋转:
![]()
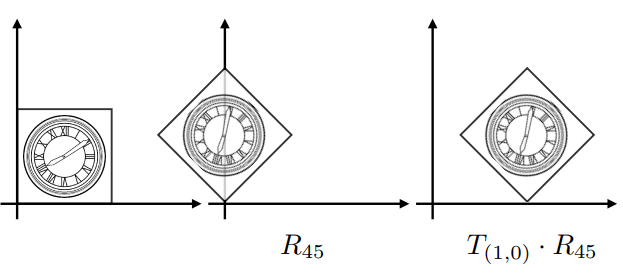
举例2 : 先旋转后平移
![]()
通过上面两个例子即可发现,及时相同的变换,但是变换的先后次序不同,将会得到不同的结果。因此带来了关于变换顺序的问题:
\[R_{45} \cdot T_{1,0} \not= T_{1,0} \cdot R_{45}
\]
(2)写变换的矩阵排列的正确顺序是:从右到左
对于举例2中的矩阵计算顺序:
![]()
由此,可得出第(3)点仿射变换序列。
(3)仿射变换序列
![]()
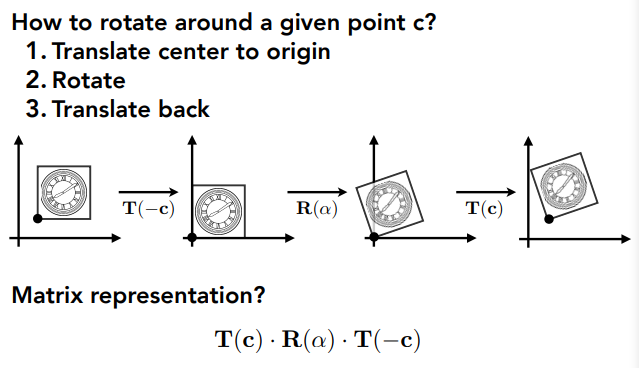
( 六 )分解复杂变换
矩阵表达:变换的矩阵==》从右至左写,原始矩阵写在最右边。
![]()
![]()
![]()
答案:变换顺序===》先线性变换再平移。





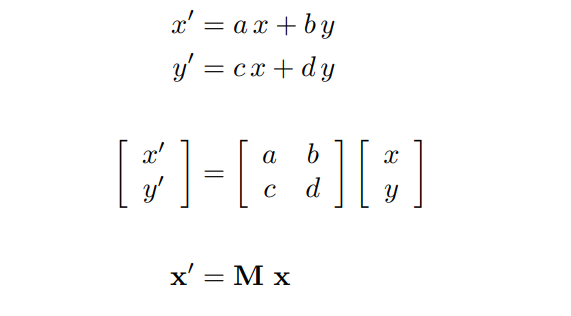
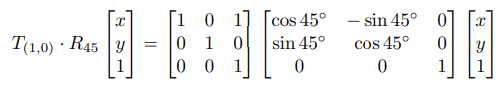
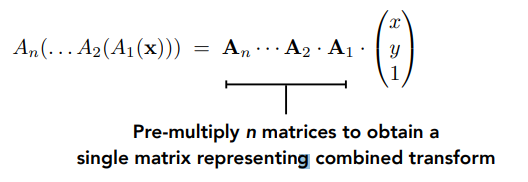
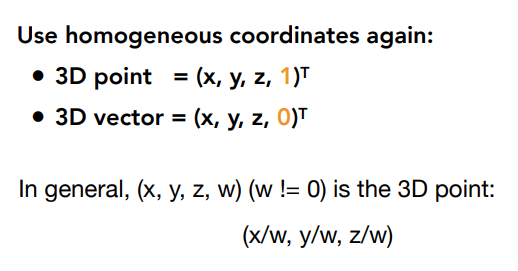


 浙公网安备 33010602011771号
浙公网安备 33010602011771号