Lecture02_向量与线性代数_GAMES101 课堂笔记——2020.2.14

一、向量(Vectors)

     向量表示示意图：

• 有序实数组，用以表示在不同坐标轴上的投影长度
• 有行和列两种表达方式，在图形学中常以列表达
• 代表了一个有方向的长度
• 基本运算：
  • 加法（满足结合律和交换律）
  • 标量乘以向量（满足结合律和分配率）
  • 点乘（内积，结果为标量，几何意义是 [公式] ，满足分配率和交换律，可用于判断两向量夹角，求向量长度，计算投影等）
  • 叉乘（外积，结果为向量，垂直于原向量构建的平面，长度为 [公式] ，交换叉乘中两向量的位置，会得到长度相同但方向相反的向量）
  • 向量归一化：p的归一化向量q与p方向相同，长度为1，可通过点乘算出

（一）向量归一化

     向量长度表示：\(||\vec a||\)
     单位向量：

• 长度 = 1
• 计算公式：

\[\hat a = \frac{\vec a}{||\vec a||} \]

• 可用于代表方向

（二）向量相加

     向量相加示意图：

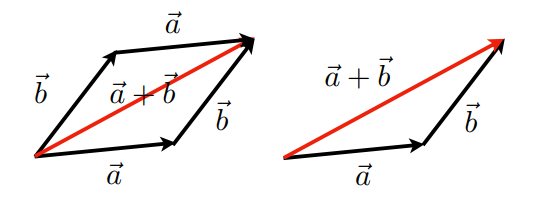
• 几何：遵守平行法则、三角法则
• 代数上：坐标相加

（三）笛卡尔积

     向量相加示意图：

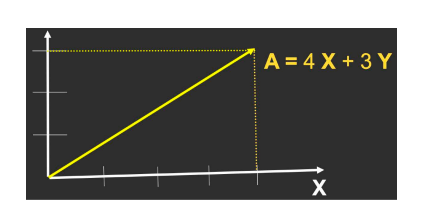
    X和Y可以是任何(通常是正交的单位)向量，

\(A = {x \choose y }\)      \(A^T = \left(x,y \right )\)      \(||A|| = \sqrt{x_2+y_2}\)

（四）向量相乘

1. 点乘

     向量点乘示意图：

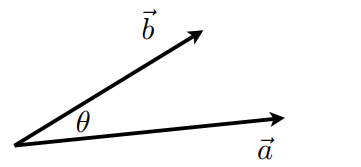
\(\vec a \cdot \vec b = \left\| \vec a \right\| \left\| \vec b \right\| \cos \theta\)     \(\cos \theta = \frac{\vec a \cdot \vec b}{\left\| \vec a \right\| \left\| \vec b \right\|}\)     
对于单位向量：\(\cos \theta = \hat a \cdot \hat b\)

（1）点乘性质

\(\vec a \cdot \vec b = \vec b \cdot \vec a\)
\(\vec a \cdot \left( \vec b + \vec c \right) = \vec a \cdot \vec b + \vec a \cdot \vec c\)
\(\left( k \vec a \right) \cdot \vec b = \vec a \cdot \left( k \vec b \right) = k \left( \vec a \cdot \vec b \right)\)

（2）在笛卡尔坐标系中做点积
     组合相乘，然后相加。

• 二维坐标系

\[\vec a \cdot \vec b = {x_a \choose y_a} \cdot {x_b \choose y_b} = x_aX_b+y_ay_b \]

• 三维坐标系

\[\vec a \cdot \vec b = \begin{pmatrix} x_a \\ y_a \\ z_a \end{pmatrix} \cdot \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix} = x_ax_b+y_ay_b+z_az_b \]

（3）投影点积
    示意图：

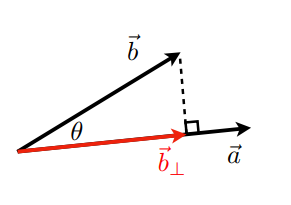
• \(\vec b_\bot\):\(\vec b\)在\(\vec a\)上的投影
  • \(\vec b_\bot\)必须属于\(\vec a\)(或者属于\(\hat a\))
    • \(\vec b_\bot = k \vec a\)
  • 求k的值
    • \(k = \left\| \vec b_\bot \right\| \cos \theta\)

（4）图形学中的点乘

• 求两个向量的夹角，(例如:光源与表面夹角的余弦值)
• 求一个向量在另一个向量上的投影

应用
测量两个向量的方向
1）在一个圆中

    例如，图中\(\vec a \cdot \vec b >0\)属于前向（forward），\(\vec a \cdot \vec c <0\)属于后向（backward）

2）两个向量之间

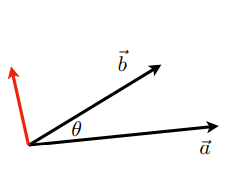
（四）向量叉乘（Cross product）

    向量叉乘示意图：

• 叉乘正交于两个原始向量
• 方向遵循右手法则，（一般默认是右手法则，即：\(\vec x \times \vec y = + \vec z\),但是OpenGL默认是左手法则，即：\(\vec x \times \vec y = - \vec z\)）
• 可用于构建坐标系

1. 叉乘性质

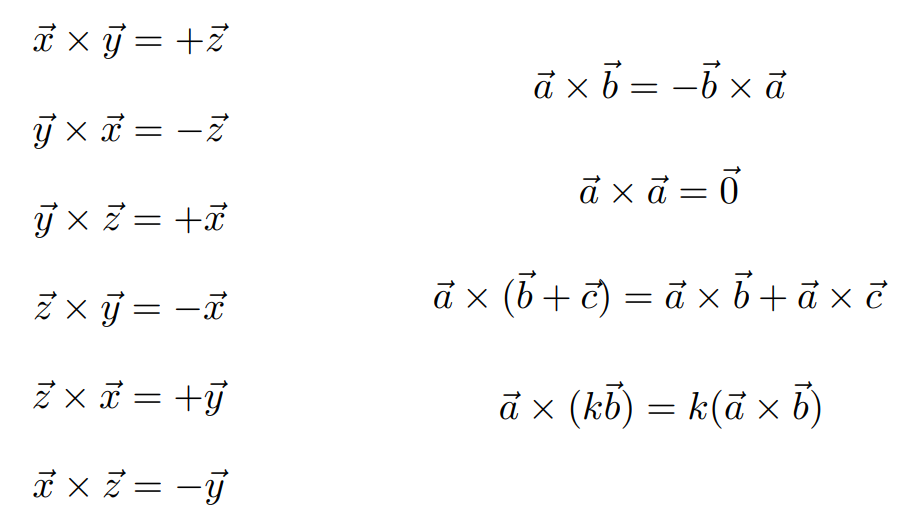
2. 叉乘：笛卡尔法则

3. 图形学中的叉乘

• 决定方向：左 or 右
  
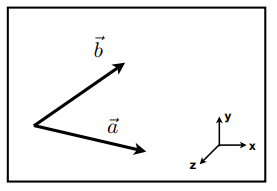
      两个向量进行叉乘，比如：\(\vec a \times \vec b >0\)，所以，\(\vec a\)在\(\vec b\)的顺时针方向（也为：右边）；\(\vec b \times \vec a <0\),所以，\(\vec b\)在\(\vec a\)的逆时针方向（也为：左边），如果\(\vec b \times \vec a = 0\)，那么\(\vec a\)则与\(\vec b\)共线。后期如果更为细致，还可以用在游戏中判断两个物体的具体方位，比如以自身正对的方向，判断敌人是在自己的左上、左下、右上、右下等位置

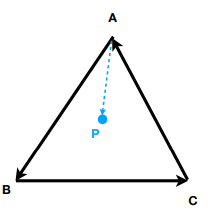
• 判断内部 or 外部
  
      如上图，若\(P\)点在三角形内部，则从同一个端点出发的边（eg:\(\vec{AB}\)）与到\(P\)点的向量（eg:\(\vec{AP}\)）,按此顺序判断（即边向量顺序连接），则P点只会在三条边的同一个方向；若在外部，P点相对于三个边的位置将不一致。

注：即使A、B、C调换顺序，按照首尾连接，效果一致。此方法可应用在光线追踪中。

• 建立坐标系
  
      叉乘后的另一个向量必定与原来两个向量垂直。

（五）标准正交基和坐标系（Orthonormal bases and coordinate frames）

1. 用途

• 对于表示点、位置、位置非常重要
• 通常有很多坐标系
  • 全球、本地、世界、模型、模型部分(头，手,…)
• 关键问题是在这正交基和坐标系之间进行转换（见Lecture03笔记）

2. 直角坐标系

    定义一个三维直角坐标系\(（u,v,w）\)：
\(\left\| \vec u \right\| = \left\| \vec v \right\| = \left\| \vec w \right\| = 1\)
\(\vec u \cdot \vec v = \vec v \cdot \vec w = \vec u \cdot \vec w = 0\)
\(\vec w = \vec u \times \vec v\) (右手法则)
\(\vec p = \left( \vec p \cdot \vec u \right) + \left( \vec p \cdot v \right) \vec v + \left( \vec p \cdot \vec w \right) \vec w\)(projection)

二、矩阵（Matrix）

    在图形学中，广泛用于变换、旋转、剪切、缩放等（详见Lecture03笔记）

• 矩阵&标量值相乘/相加：每个元素相乘/相加。
• 矩阵&矩阵相乘：\(\left(M \times N \right) \left( N \times P \right)\),要求前一个的列数 = 后一个矩阵的行数。

矩阵&向量 相乘

• 把向量当做一个列矩阵\(\left( m \times \right)\)
• 关于y轴的2D反射

\[\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -x \\ y \end{pmatrix} \]

1. 矩阵转置

\[\begin{pmatrix} 1 & 2 \\ 6 & 4 \\ 5 & 6 \end{pmatrix}^T = \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{pmatrix} \]

-矩阵转置的性质

\[\left( AB \right)^T = B^TA^T \]

2.单位矩阵和逆变换

\(I_{3 \times 3} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}\)

\(AA^{-1} = A^{-1}A = I\)

\(\left( AB \right)^{-1} = B^{-1}A^{-1}\)

3. 矩阵形式中的向量相乘

• 点乘：

\[\vec a \cdot \vec b = {\vec a}^T \vec b = \begin{pmatrix} x_a & y_a & z_a \end{pmatrix} \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix} = \left(x_ax_b + y_ay_b + z_az_b \right) \]

• 叉乘：

\[\vec a \times \vec b = A * b = \begin{pmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0 \end{pmatrix} \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix} \]