【题解笔记】PTA基础6-7：统计某类完全平方

题目地址：https://pintia.cn/problem-sets/14/problems/739

前言

咱目前还只能说是个小白，写题解是为了后面自己能够回顾。如果有哪些写错的/能优化的地方，也请各位多指教。( •̀ ω •́ )

题目描述

本题要求实现一个函数，判断任一给定整数N是否满足条件：它是完全平方数，又至少有两位数字相同，如144、676等。

展开查看详情

函数接口定义

int IsTheNumber ( const int N );

其中N是用户传入的参数。如果N满足条件，则该函数必须返回1，否则返回0。

裁判测试程序样例

#include <stdio.h>
#include <math.h>

int IsTheNumber ( const int N );

int main()
{
    int n1, n2, i, cnt;
    
    scanf("%d %d", &n1, &n2);
    cnt = 0;
    for ( i=n1; i<=n2; i++ ) {
        if ( IsTheNumber(i) )
            cnt++;
    }
    printf("cnt = %d\n", cnt);

    return 0;
}

/* 你的代码将被嵌在这里 */

输入样例

105 500

输出样例

cnt = 6

限制

限制内容	限制条件
代码长度限制	16 KB
时间限制	400 ms
空间限制	64 MB

想法

注：完全平方数指的是一个可以由 某一个整数的平方 表达的数。

判断完全平方数

首先观察给出的裁判测试程序样例，发现程序在预处理部分引入了math.h，很明显，要判断完全平方数，我们得用到math.h头文件中声明的sqrt()（开平方根）函数：

double sqrt ( double arg );

该函数返回的是一个双精度浮点数，如果其小数部分为0，则说明该数是完全平方数。

这样想，其实将sqrt()函数的返回值转换为整型，将这个整型的平方和原数进行比较，就可以判断是否为完全平方数了：

int squareRoot = (int) sqrt(N);
if (squareRoot * squareRoot == N) {
    // N是完全平方数
}

---

我最开始用了种危险的写法：

double squareRoot = sqrt(N);
if (squareRoot == (int) squareRoot) {
    // N是完全平方数
}

运行起来可能不会出问题，但实际上是有隐患的。这里的逻辑其实是在将整型和浮点型在进行比较，而计算机中的浮点数储存是不精确的，不要这样写。

至少有两位数字相同

虽然题目中给出的样例数都是三位数，但是PTA吧，肯定不会这么容易就让我过，那我肯定要再上升一层进行思考。

我的想法是从最低位开始，用数组储存每一位的数字。而在每次迭代中，将当前位的数字与数组中的每一位进行比较，只要遇到相同的，就能保证至少有两位数字相同：

// 判断整数number中是否至少有两位数字相同
int HasTwoSameNum(const int number) {
    int quotient = number; // 商
    int remainder; // 余数
    int arrLen = 0;
    int arr[10]; // int型最多10位数字
    int i;
    while (quotient > 0) {
        remainder = quotient % 10; // 余数
        quotient = quotient / 10; // 商
        for (i = 0; i < arrLen; i++) {
            if (arr[i] == remainder)
                return 1;
        }
        arr[arrLen++] = remainder;
    }
    return 0;
}

为什么定义数组时将元素个数定为10呢？因为题目中处理的数据类型是整型。

目前来说，一般的计算机中一个整型int占用4个字节，即32位，而32位的整型在计算机储存时要用到31个二进制位来表示数值（最高位表示符号），因此int的取值范围是-2^31到2^31-1，即-2147483648到2147483647。

很明显，题目关注的是十进制数，观察2147483648能发现，int型的整数在十进制下最多只有10位，所以我才将数组的元素个数定为10。

---

关于提取整数的每一位数字这部分，实际上用取模和取整就可以实现。

上述代码中，quotient % 10能得到quotient的最低位数字；而quotient / 10能得到quotient除去最低位数字的整数，这个数值就是下一次迭代的quotient。

迭代至quotient为0时，就已经把原整数中的每一位数都取遍了。

题解代码

OJ端提交的代码：

int HasTwoSameNum(const int number) {
    int quotient = number; // 商
    int remainder; // 余数
    int arrLen = 0;
    int arr[10]; // int型最多10位数字
    int i;
    while (quotient > 0) {
        remainder = quotient % 10; // 余数
        quotient = quotient / 10; // 商
        for (i = 0; i < arrLen; i++) {
            if (arr[i] == remainder)
                return 1;
        }
        arr[arrLen++] = remainder;
    }
    return 0;
}

int IsTheNumber(const int N) {
    int squareRoot = (int) sqrt(N);
    // 如果平方根都不是，就没必要调用HasTwoSameNum了
    if (squareRoot * squareRoot == N && HasTwoSameNum(N))
        return 1;
    else
        return 0;
}

本地测试可用：

#include <stdio.h>
#include <math.h>

int IsTheNumber(const int N);

int HasTwoSameNum(const int number);

int main() {
    int number;
    printf("Input an integer: ");
    fflush(stdout);
    scanf("%d", &number);
    printf("IsTheNumber = %d\n", IsTheNumber(number));

    return 0;
}

int HasTwoSameNum(const int number) {
    int quotient = number; // 商
    int remainder; // 余数
    int arrLen = 0;
    int arr[10]; // int型最多10位数字
    int i;
    while (quotient > 0) {
        remainder = quotient % 10; // 余数
        quotient = quotient / 10; // 商
        for (i = 0; i < arrLen; i++) {
            if (arr[i] == remainder)
                return 1;
        }
        arr[arrLen++] = remainder;
    }
    return 0;
}

int IsTheNumber(const int N) {
    int squareRoot = (int) sqrt(N);
    // 如果平方根都不是，就没必要调用HasTwoSameNum了
    if (squareRoot * squareRoot == N && HasTwoSameNum(N))
        return 1;
    else
        return 0;
}

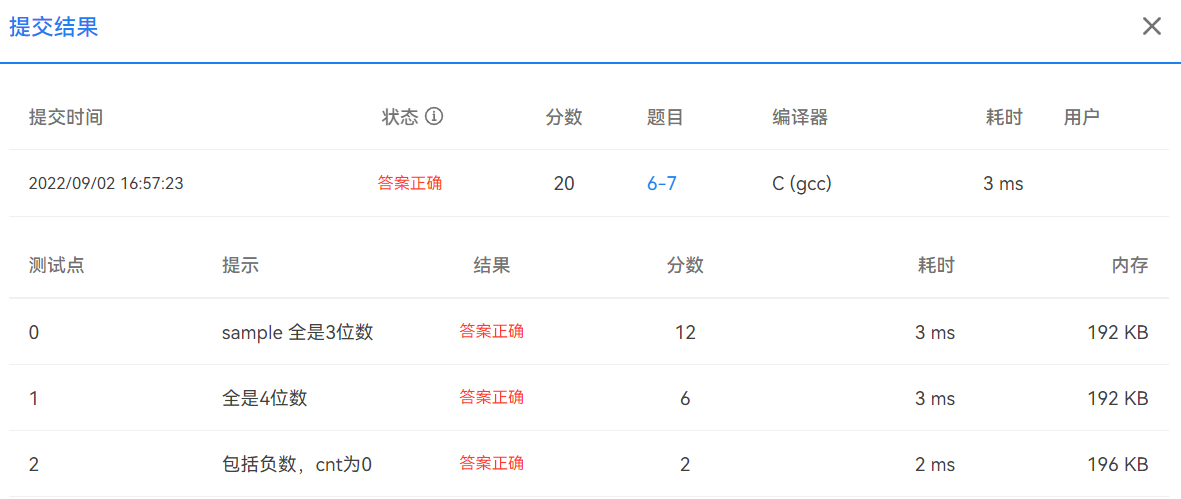
提交结果