【题解笔记】PTA基础6-10:阶乘计算升级版
题目地址:https://pintia.cn/problem-sets/14/problems/742
前言
咱目前还只能说是个小白,写题解是为了后面自己能够回顾。如果有哪些写错的/能优化的地方,也请各位多指教。( •̀ ω •́ )
题目描述
本题要求实现一个打印非负整数阶乘的函数,要求能处理一定大数值的阶乘。
展开查看详情
函数接口定义
void Print_Factorial ( const int N );
其中N是用户传入的参数,其值不超过1000。如果N是非负整数,则该函数必须在一行中打印出N!的值,否则打印"Invalid input"。
裁判测试程序样例
#include <stdio.h>
void Print_Factorial ( const int N );
int main()
{
int N;
scanf("%d", &N);
Print_Factorial(N);
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例
15
输出样例
1307674368000
限制
| 限制内容 | 限制条件 |
|---|---|
| 代码长度限制 | 16 KB |
| 时间限制 | 400 ms |
| 空间限制 | 64 MB |
想法
怎么储存如此之大的阶乘结果
不看不知道,细看吓一跳,题目中对N的限制是0<=N<=1000,得想个办法让程序储存1000!这么大的一个数。
扫视了一圈C语言的基本数据类型,就连unsigned long long类型也远存不下1000的阶乘。
转换一下思路。数字每一位之间都是紧挨在一起的,我们其实可以采用一种连续的数据结构来储存这个结果,比如....数组!
设数组第一个元素表示个位,第二个元素表示十位...以此类推。这样一来,我们就可以用数组以数位升序来储存这个大数了。最后只需将数组中的每个元素(int)打印到屏幕上即可。
给数组分配多少个元素
题目的裁判测试程序并没有引入stdlib.h头文件,因此我没法使用动态内存分配/回收函数。而1000!的结果到底有多少位,我一时半会儿也是不知道的。
其实可以用最简单粗暴的方式估计一下:1000个1000相乘
这样算出来的结果有3001位。如果是运算1000!的话,是怎么也不会算出3001个数位的数字的,所以分配3000个元素一定能保证数组能装得下结果的所有数位。
注:有一种可以用来计算阶乘近似值的公式——斯特林公式
实现乘法时关注的对象
阶乘运算的基础是乘法运算,只要把正确的乘法算法写出来,这道题咱们就几乎能解决了!
关于乘法算法,我觉得要关注以下三种情况:
-
无需进行进位操作
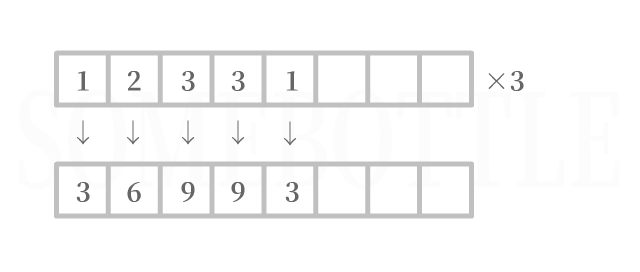
每一位数字乘上因数后均未超过
9,无需进位。 -
需要进行进位操作
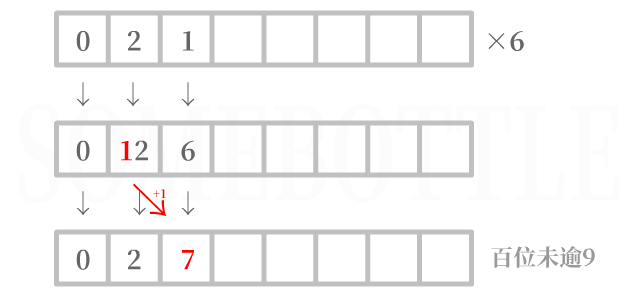
假设当前处理的是十位,十位数字乘上因数后为
12,超过了9。将12“拆成”1和2,将最低位2保留下来,其余的数位1进入高位。
-
需要进行进位操作,而且进了一位后的数位又可以再进一位
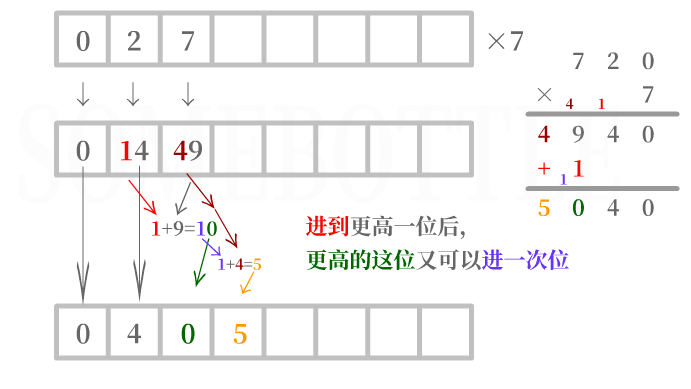
假设当前处理的是百位,百位数字乘上因数后为
49,超过了9。将49“拆成”4和9,将最低位9保留下来,其余的数位4进入高位。然而此时发现,之前在处理十位时,十位上的数字被拆分为
1和4,其中1进入到百位,而百位现在的数字是9,9+1又可以向后进一位。9+1=10,因此将0保留下来,而1进入高位,加上之前进入高位的数字4,现在进入高位的数字是4+1=5。注:这是很容易被忽略的一种情况。
根据以上描述,可以发现在每次迭代中,我关注的是:
- 当前处理的数位
- 进入到下一位的数值
处理乘法中的进位
上面给出的演示中,进入高位的数字都没有超过9,那么如果要进入高位的数字超过了9怎么办呢?
实际上这里和上面的处理方法是差不多的。
每次迭代中处理进到当前数位的数值时,将待进位的数值中的最低位进到当前的数位,在去除待进位的数值中的最低位后,剩余的数值留到后面处理更高位的进位。
咱做了一个动图来直观地演示一下这个过程:
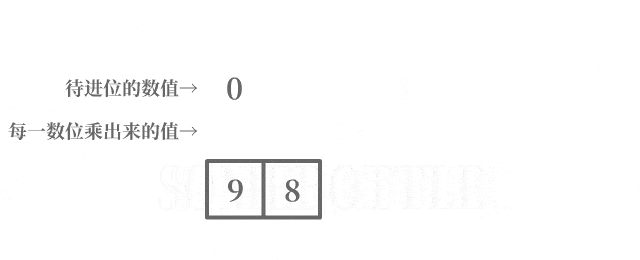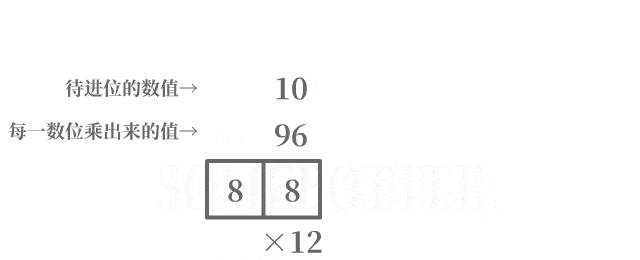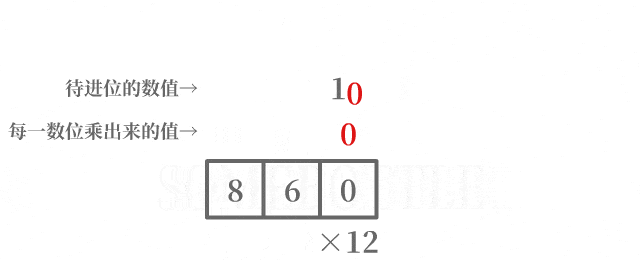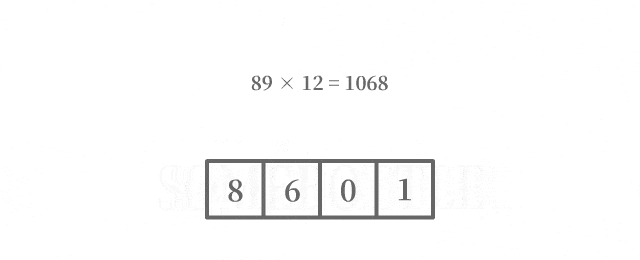
代码实现乘法部分
这里只截取了乘法部分,完整代码可以看下方题解代码
// arr是按数位储存结果的数组
// arrLen是上述数组的长度,也代表了结果数值的位数
// factor是每次迭代中要乘上的因数
// 将数组每一位都乘i,并进行进位处理(超过9的数字往高处进)
int j;
int carry = 0; // 要进到高位的数字
int multiplied; // 用于临时储存数组中每一位数字乘了因数之后的值
int calcDigit; // 用于临时储存新计算出来的某一个数位
for (j = 0; j < arrLen; j++) {
multiplied = arr[j] * factor; // 每一位都乘i
// multiplied % 10 取 <当前数位×因数> 的最低位,比如6*3=18>9,这个时候取出8,而1要进到高位
// carry % 10 将 <上一次迭代留给本次迭代进位的数值> 的最低位取出,这一位是进到 <当前正在处理的数位> 的
calcDigit = multiplied % 10 + carry % 10;
// 运算留给 <下一次迭代> 进位的数值(carry)
// 将 <进到当前数位的值> 去掉最低位(因为最低位在上面已经进到当前数位了),加上multiplied要进到高位的数字
carry = carry / 10 + multiplied / 10;
// 一种很容易错的情况,虽然multiplied % 10和carry % 10分别不会>=10,但是他们加起来是可能>=10的!
// 也就是说,当前处理的数位在进位后可能>=10,需要再处理一道
// 这种时候还要再进一次位
if (calcDigit >= 10) {
// 将除最低位外的数位加到 <下一次迭代> 进位的数值(carry)上
carry += calcDigit / 10;
// 当前数位只保留最低位
calcDigit %= 10;
}
// 存入最终运算出来的当前数位的值
arr[j] = calcDigit;
// j到数组边界了,但是还有要进到高位的数值,这说明位数不够了,那么就增加位数(增加数组元素)
if (j >= arrLen - 1 && carry > 0)
arrLen++;
}
题解代码
部分正确
这部分正确的代码错就错在忽略了当前数位的二次进位问题。
展开查看详情
void Print_Factorial(const int N) {
if (N < 0) {
printf("Invalid input");
return;
}
int arr[3000] = {};
arr[0] = 1;
int arrLen = 1;
int factor = 2;
for (; factor <= N; factor++) {
int j;
int carry = 0;
int multiplied;
for (j = 0; j < arrLen; j++) {
multiplied = arr[j] * factor;
arr[j] = multiplied % 10 + carry % 10;
carry = carry / 10 + multiplied / 10;
// 这里少考虑了一种情况
if (j >= arrLen - 1 && carry > 0)
arrLen++;
}
}
int i;
for (i = arrLen - 1; i >= 0; i--) {
printf("%d", arr[i]);
}
}
Accepted的代码
void Print_Factorial(const int N) {
if (N < 0 || N > 1000) {
printf("Invalid input");
return;
}
/*
如果阶乘结果大到C语言中任意一种基本数据类型都无法表达,
不妨考虑一下能不能用某种数据结构来解决问题
这里采用数组
*/
/* 1000个1000相乘:1*(10^(3*1000))=1e+3000,
结果是1000000000....(3000个零)
而本题N不超过1000,阶乘结果肯定也达不到1e+3000,
这里就给数组分配3000个元素
*/
// 从数组第一个元素为个位开始,往后数位升高
int arr[3000] = {}; // 全初始化为0
arr[0] = 1; // 个位为1
int arrLen = 1; // 标记数组目前元素个数(结果位数)
int factor = 2; // 从2开始乘,因为arr[0]=1
for (; factor <= N; factor++) {
int j;
int carry = 0;
int multiplied;
int calcDigit;
for (j = 0; j < arrLen; j++) {
multiplied = arr[j] * factor;
calcDigit = multiplied % 10 + carry % 10;
carry = carry / 10 + multiplied / 10;
if (calcDigit >= 10) {
carry += calcDigit / 10;
calcDigit %= 10;
}
arr[j] = calcDigit;
if (j >= arrLen - 1 && carry > 0)
arrLen++;
}
}
// 打印结果数字
int i;
// 因为随着下标增加,数位升高,要打印出来正常的数值就得倒着遍历数组
for (i = arrLen - 1; i >= 0; i--) {
printf("%d", arr[i]);
}
}
C++代码实现
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n;
cin >> n; // 注意题目中说n为正整数,不用考虑0!的情况了
vector<short> result{1}; // 用一个vector容器按**从低位到高位**的顺序储存结果每一位数字
int digitsNum = 1; // 储存位数,而不是老是用vector的size方法
for (int factor = 2; factor <= n; factor++) // 从2开始乘
{
int carry = 0; // 进位数
int currDigit = 0; // 当前处理到的位数
do
{
int mulDigit = 0;
if (currDigit < digitsNum) // 不需要新增数位
{
mulDigit = result[currDigit] * factor; // 算出当前位乘上因子的结果
}
else
{ // 新增一位(在进位的时候会发生这种情况)
result.push_back(0);
digitsNum++;
}
int newDigit = mulDigit % 10 + carry % 10; // 将carry的最低位加上上面结果(mulDigit)的最低位,得到当前位的新值
carry = carry / 10 + mulDigit / 10; // 更新carry,除去最低位,并加上(multDigit)除最低位外的数
if (newDigit > 9)
{
// 进位后,新的一位又>9了,需要再进到高位
carry += newDigit / 10;
newDigit = newDigit % 10;
}
result[currDigit] = (short)newDigit; // 更新当前位
currDigit++; // 处理下一位
} while (currDigit < digitsNum || carry != 0); // 位数没处理完,或者还有进位,循环就要继续
}
for (int i = digitsNum - 1; i >= 0; i--)
{
cout << result[i];
}
return 0;
}
提交结果截图
-
WA
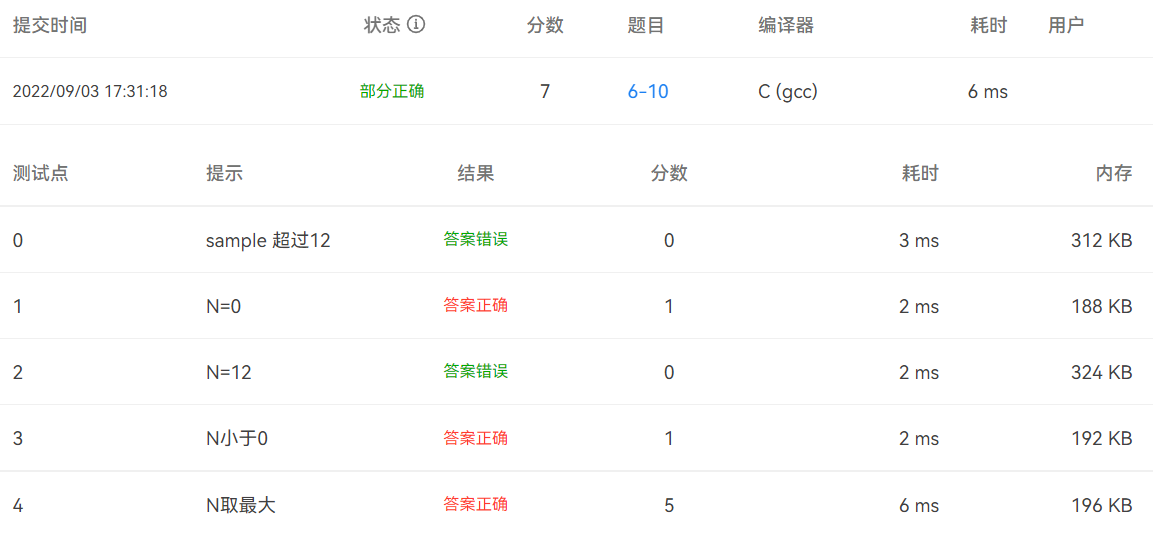
-
AC


 浙公网安备 33010602011771号
浙公网安备 33010602011771号