莫比乌斯反演总结

目录

• 莫比乌斯函数
  • 定义
  • 性质一
  • 性质二
• 莫比乌斯反演
  • 莫比乌斯反演
  • 变形一
  • 变形二
• 应用

莫比乌斯函数

定义

莫比乌斯函数 \(\mu (n)\) 的定义为：设 \(n = p_1^{k_1} \cdot p_2^{k_2} \cdot \cdots \cdot p_m^{k_m}\) ，其中 \(p\) 为素数，则定义如下：

\[\mu(n)= \begin{cases} 1& n = 1\\ (-1)^m& \prod_{i=1}^{m} k_i = 1 \\ 0& \text{otherwise}(k_i > 1) \end{cases} \]

性质一

性质一  莫比乌斯函数是积性函数，即 \(\mu(a \cdot b) = \mu(a) \cdot \mu(b)\) ，其中 \(a\) 和 \(b\) 互质。

应用  根据这一性质，我们可以采取线性筛法，用 \(O(n)\) 的时间复杂度预处理出 \([1,n]\) 内的莫比乌斯函数值。

质数的值为 \(-1\) ，如果一个数存在某个质因子的指数不为 \(1\) ，那么它将会被筛为 \(0\) 。

void init(){
    mu[1] = 1;
    int tot = 0;
    for(int i = 2; i <= maxn; i++){
        if (!check[i]) {
            mu[i] = -1;
            prime[++tot] = i;
        }
        for(int j = 1; j <= tot && i * prime[j] <= maxn; j++){
            check[i * prime[j]] = 1;
            if(i % prime[j] == 0) break;
            mu[i * prime[j]] = -mu[i];
        }
    }
}

性质二

性质二 \(\sum_{d|n}\mu[d]=[n=1]\)

证明

当 \(n = 1\) 时，\(\mu(1)=1\) 显然成立。

否则设 \(n = p_1^{k_1} \cdot p_2^{k_2} \cdot \cdots \cdot p_m^{k_m}\) ，\(d = p_1^{x_1} \cdot p_2^{x_2} \cdot \cdots \cdot p_m^{x_m}\) 。根据 \(\mu\) 的定义，只需考虑 \(x_i=0\) 或 \(x_i=1\) 的情况。设 \(d\) 中存在 \(r_i\) 个 \(x_i\) 等于 \(1\) ，我们有：

\[\sum_{d|n}\mu(d) = \sum_{r=0}^{m} \binom{m}{r}(-1)^r \]

根据二项式定理：

\[(x+y)^n = \sum_{k=0}^{n} \binom{n}{k} x^{n-k}y^{k} \]

我们令 \(x=1,\ y=-1\) ，即有：

\[\sum_{r=0}^{m} \binom{m}{r}(-1)^r = (1-1)^m=0 \]

综上，得证。

莫比乌斯反演

莫比乌斯反演

设 \(f(n),\ g(n)\) 时数论函数，且满足 \(f(n) = \sum_{d|n} g(d)\) ，则有莫比乌斯反演：

\[g(n) = \sum_{d|n} \mu(\frac{n}{d})f(d) = \sum_{d|n} \mu(d) f(\frac{n}{d}) \]

数论函数 在数论上，算术函数（或称数论函数）指定义域为正整数、值域为复数的函数，即 \(f:\mathbb {Z} ^{+}\rightarrow \mathbb {C}\) 。每个算术函数都可视为复数的序列。最重要的算术函数是积性及加性函数。

证明

\[\begin{split} \sum_{d|n} \mu(d) f(\frac{n}{d}) &= \sum_{d|n} \mu(d) \sum_{i|\frac{n}{d}} g(i) \\ &= \sum_{i|n} g(i) \sum_{d|\frac{n}{i}} \mu(d) \end{split}\]

• 当 \(i = n\) 时，\(g(i)\sum_{d|\frac{n}{i}} \mu(d) = g(n)\) 。
• 当 \(i < n\) 且 \(i\) 是 \(n\) 的因数时，根据 \(\sum_{d|n}\mu[d]=[n=1]\) 可得 \(\sum_{d|\frac{n}{i}}=0\)，乘 \(g(i)\) 也为 \(0\) 。

综上，得证。

变形一

\[f(i)=\sum_{d=1}^{\lfloor{\frac{n}{i}} \rfloor} g(d\cdot i) \Rightarrow g(i) = \sum_{d = 1}^{\lfloor{\frac{n}{i}} \rfloor} f(d\cdot i)\mu(d) \]

证明

我们将 \(f(d\cdot i)\) 展开得：

\[g(i) = \sum_{d = 1}^{\lfloor{\frac{n}{i}} \rfloor} f(d\cdot i)\mu(d) = \sum_{d = 1}^{\lfloor{\frac{n}{i}} \rfloor} \mu(d) \sum_{j=1}^{\lfloor \frac{n}{d\cdot i} \rfloor} g(j\cdot d\cdot i) \]

我们令 \(t = j\cdot d\) ，那么有：

\[\sum_{d = 1}^{\lfloor{\frac{n}{i}} \rfloor} \mu(d) \sum_{j=1}^{\lfloor \frac{n}{d\cdot i} \rfloor} g(j\cdot d\cdot i) = \sum_{t=1}^{\lfloor \frac{n}{i} \rfloor} g(t\cdot i)\sum_{d|t}\mu(d) \]

根据 \(\sum_{d|n}=[n=1]\) 易得：上式等于 \(g(i)\)。

变形二

\[f(i) = \sum_{i|d}g(d) \Rightarrow g(i) = \sum_{i|d}f(d)\cdot\mu(\frac{d}{i}) \]

证明

我们令 \(\frac{d}{i} = k\) ，那么有：

\[\begin{split} \sum_{i|d}f(d)\cdot\mu(\frac{d}{i}) &= \sum_{k=1}^{\infty}\mu(k)f(k\cdot i) \\ &= \sum_{k=1}^{\infty}\mu(k) \cdot \sum_{k\cdot i | t} g(t) \\ &= \sum_{i|t}g(t)\sum_{k|\frac{t}{i}}\mu(k) \end{split}\]

根据 \(\sum_{d|n}\mu[d]=[n=1]\) 易得：上式等于 \(g(i)\)。

应用

问题 求 \(\gcd = k\) 的个数

\[\sum_{i=1}^{n}\sum_{j=1}^{m}[\gcd(i,j) = k] \]

设 \(f(x)\) 为 \(\gcd(i,j)=k\) 的个数，\(g(k)\) 为满足 \(k\ |\ \gcd(i,j)\) 的对数，则有以下关系：

\[g(k) = \sum_{x=1}^{\lfloor \frac{n}{k} \rfloor} f(k\cdot x) \]

我们只需快速求出 \(g(k)\) 。易得，如果 \(i,j\) 能被 \(k\) 整除，那么他们可以写成 \(i = k\cdot x_1;\ j=k\cdot x_2\) 的形式，我们之需求有多少对 \(x_1,x_2\) 即可，有：

\[g(k) = \lfloor \frac{n}{k} \rfloor \lfloor \frac{m}{k} \rfloor \]

根据莫比乌斯反演变形一我们有：

\[\begin{split} f(k) &= \sum_{x=1}^{\lfloor \frac{n}{k} \rfloor} \mu(x)g(x\cdot k) \\ &= \sum_{x=1}^{\lfloor \frac{n}{k} \rfloor} \mu(x) \lfloor \frac{n}{kx} \rfloor \lfloor \frac{m}{kx} \rfloor \end{split}\]

\(f(k)\) 就是答案，暴力求解的时间复杂度为 \(O(n)\) 。

分块优化

这里提出一个分块的思想：\(\lfloor \frac{n}{d} \rfloor\) 有至多 \(O(\sqrt{n})\) 个取值。

证明

• 当 \(1 \le d \le \sqrt{n}\) 时，由于 \(d\) 只有 \(\sqrt{n}\) 个，所以 \(\lfloor \frac{n}{d} \rfloor\) 只有至多 \(\sqrt{n}\) 个取值。
• 当 \(\sqrt{n} \le d \le n\) 时，由于 \(\lfloor \frac{n}{d} \rfloor\) 小于 \(\sqrt{n}\) ，所以 \(\lfloor \frac{n}{d} \rfloor\) 只有至多 \(\sqrt{n}\) 个取值。

得证，\(\lfloor \frac{n}{d} \rfloor\) 只有至多 \(O(\sqrt{n})\) 个取值。

同理 \(\lfloor \frac{m}{d} \rfloor\) 只有至多 \(\sqrt{m}\) 个取值。又因为取值时连续的，所以 \(\lfloor \frac{n}{kx} \rfloor\) 和 \(\lfloor \frac{m}{kx} \rfloor\) 同时不变的数据段有 \(O(\sqrt{n} + \sqrt{m})\) 个。

例如：\(n = 32, m = 40, k = 2\) ，红色为相等的段。

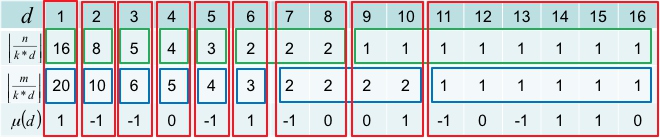
对于相等的段，我们求取 \(\mu\) 的前缀和，即可批量计算这一个段的答案，从而降低时间复杂度。

ll F(int n, int m, int d){
    if (n > m) swap(n, m);
    ll ans = 0;
    n /= d, m /= d;
    for (int i = 1, last = 1; i <= n; i = last + 1) {
        last = min(n / (n / i), m / (m / i));
        ans += (ll)(sum[last] - sum[i - 1]) * (n / i) * (m / i);
    } 
    return ans;
}

对于位置 \(i\) ，找到下一个相等的位置为last = min(n / (n / i), m / (m / i));。

时间复杂度为 \(O(\sqrt{n} + \sqrt{m})\) 。