c++算法学习笔记
c++算法学习笔记
变量的直接初始化
变量的直接初始化对于C++语法是一个重要的功能，可以用来初始化变量
class Data{
public:
Data():m_map({{1,2},{3,4}}){}
void printMap()
{
for_each(m_map.begin(), m_map.end(), [](auto& pair){
cout << pair.first << pair.second << endl;
})
}
private:
map<int, string> m_map;
};
map的直接初始化方式为map({{},{}})或者map{{},{},{}}
算法纪要
1、能用递归就不用栈，能用stl就一定不自己实现
2、不提倡防御式编程，不校验malloc/new返回的指针是否为nullptr，不许检查内部函数入口，参数有效性
编程技巧
1、判断浮点数a和b是否相等时，不能直接用a=b，应判断fabs(a-b)是否小于某个阈值，比如1e-9
2、判断是否奇数时，使用x % 2 != 0, 不要使用x%2==1，因为可能会有负数
3、char的值作为数组下标，不太可取，因为char可能有负值
4、vector和string的使用优先于动态分配的数组
5、使用reserve避免不必要的重新分配
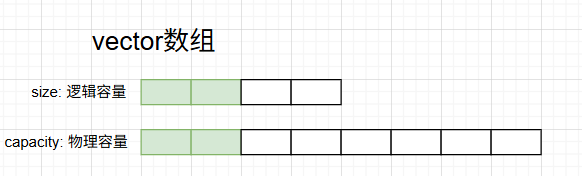
vector数组会有一个size和capacity的概念，size代表逻辑容量，capacity代表物理已经分配的内存的容量。默认初始化时，容量为1；resize()操作的逻辑容量，并不真正分配内存；reserver()操作用于操作内存容量，可以提前分配内存，避免扩容导致的性能下降。
考虑1个问题：
1、当size大于capacity时会发生什么？
此时物理分配的内存不够用，此时会触发自动扩容，扩容并非简单意义上接着扩容，而是分为三步：申请新内存通常为capacity的两倍（默认是2倍），复制旧内存区域的值到新内存区域，释放旧内存，更新capacity为新内存大小。
昨日一题
80、删除有序数组中的重复项 II
典型的双指针解法，初始化条件，更新机制
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
// 此问题中删除重复的元素，最多只能保留2次，如果小于2个元素则直接返回
if (nums.size() < 3) return nums.size();
// 本质上是要更新cnt
int cnt =2; // cnt记录新的数组位置，所以更要明确，数组该怎么更新呢
for (int i = 2; i < nums.size(); i++) {
if (nums[i] != nums[cnt-2]) { // 核心更新机制
nums[cnt++] = nums[i];
}
}
return cnt;
}
};
拓展，如果此时数组并不有序呢？答：要借助一个空间统计元素出现的次数
33、搜索旋转排序数组
本题有意思的是，旋转数组，数组从某个元素位置，旋转左边，由【0,1,2,3,4,5，6,7,8】到【4,5,6,7,8,0,1,2,3,4】
基本的二分法其实要确定数组为有序才可操作，所以此次要确定哪部分有序再进行操作。
核心理念：二分法+判断有序区间
class Solution {
public:
int search(vector<int>& nums, int target) {
// 二分法搜索，如果直接用模板算法，不会成功应该，因为实现是超时的
int left = 0, right = nums.size();
while (left != right) {
const int mid = (left + right)/2;
if (nums[mid] == target) {
return mid;
}else if (nums[left] <= nums[mid]){
if (nums[left] <= target && nums[mid] > target) {
right = mid;
}else{
left = mid + 1;
}
}else {
if (nums[mid] <= target && nums[right-1] > target) {
left = mid + 1;
}
else {
right = mid;
}
}
}
return -1;
}
};
81、搜索排序数组2
比搜索排序组，更多的是增加了相同数字，此时查询目标值，因为可能同时出现nums[l]nums[m]，l和m不同位置的情况；所以这时候需要特殊处理；当nums[l]nums[m]时，此时无法确定有序区间，l++走一步再处理；当nums[l]<nums[m]时，代表左半区此时是升序区间可以进行二分法，【l，m)；当nums[l] > nums[m]，此时【m+1，r）是升序区间，进行处理
class Solution {
public:
bool search(vector<int>& nums, int target) {
int left = 0, right = nums.size();
while (left != right) {
const int mid = (left + right)/2;
if (nums[mid] == target) {
return true;
}else if (nums[left] < nums[mid]){
if (nums[left] <= target && nums[mid] > target) {
right = mid;
}else{
left = mid + 1;
}
}else if (nums[left] > nums[mid]){
if (nums[mid] < target && nums[right-1] >= target) {
left = mid + 1;
}
else {
right = mid;
}
}else {
left++;
}
}
return false;
}
};
4、寻找两个正序数组的中位数
可以看成查找第k个元素，递归解决问题就可以。递归的终止条件是什么呢？
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
// 这道题本质上是经典问题，找第k个元素
// 实现成递归
// 如果单纯只遍历一遍数组，那么复杂度为O(m+n)
int m = nums1.size(), n = nums2.size(), total = m + n;
// 奇数和偶数要分开
if (total & 0x1) {
return findKElements(nums1.begin(), m, nums2.begin(), n, total/2 + 1);
}else {
return (findKElements(nums1.begin(), m, nums2.begin(), n, total/2) + findKElements(nums1.begin(), m, nums2.begin(), n, total/2 + 1)) / 2;
}
}
private:
double findKElements(vector<int>::const_iterator A, int m, vector<int>::const_iterator B, int n, int k) {
int ia = min(k/2, m), ib = k - ia;
// 假定m <= n, 否则交换
if (m > n) return findKElements(B, n, A, m, k);
if (m==0) return *(B + k - 1);
if (k==1) return min(*A, *B);
// 划分区域
if ( *(A + ia - 1) < *(B + ib - 1)) {
return findKElements(A + ia, m - ia, B, n, k - ia);
}else if (*(A + ia - 1) > *(B + ib - 1)) {
return findKElements(A, m, B + ib, n - ib, k - ib);
}else {
return A[ia - 1];
}
return 0;
}
};
128、最长连续序列
此题麻烦点在于时间复杂度的计算方式，为O(2n),因此时间复杂度为O(n)，无序map的查找、删除、插入效率更高。
class Solution {
public:
int longestConsecutive(vector<int>& nums) {
// 由于要求是Olog(n)，所以不能用排序后进行寻找的办法
// 所以想到用一个字典去记录
unordered_map<int, bool> m_map;
int longest = 0;
for(auto i:nums) {
m_map[i] = false;
}
for (auto i:nums) {
if (m_map[i]) continue;
int length = 1;
m_map[i] = true;
// 从元素开始向左和向右进行遍历，查询在数组中是否有连续元素存在
for (int j = i+1; m_map.find(j) != m_map.end(); ++j) {
m_map[j] = true;
length++;
}
for (int j = i-1; m_map.find(j) != m_map.end(); --j) {
m_map[j] = true;
length++;
}
longest = max(longest, length);
}
return longest;
}
};
1、 两数之和
两数只和，可以任意顺序返回答案，但是有一个问题，如果出现相同的数字两次，会怎么样，这和m_map[nums[i]] = i的放置顺序有很大关系，放在前面则先存储后查询，如果是相同的数字，则可能会存在的情况是，返回同一位置元素，但是不能返回同一位置的元素，所以必须后存储先查询
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> m_map;
for (int i = 0; i < nums.size(); ++i) {
if (m_map.find(target-nums[i]) != m_map.end() && i != m_map[target-nums[i]]) return {i, m_map[target-nums[i]]};
m_map[nums[i]] = i;
}
return {};
}
};
15、三数之和
本体的解决的是，三数之和问题
时间复杂度为O(n2)
夹逼，进行解决问题，可以获取特定值
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
// 三数之和，最差的是三个次方的时间复杂度，但是可以通过夹逼进行解决, 先排序再夹逼才是对的
vector<vector<int>> result;
const int target = 0;
sort(nums.begin(), nums.end());
for (auto i = nums.begin(); i < nums.end() - 2; ++i) {
// 从两边进行夹逼
auto j = i + 1;
auto k = nums.end() -1;
// 解决相同i的问题
if (i > nums.begin() && *i == *(i - 1)) continue;
// 开始夹逼，从左和右
while(j < k) {
if (*i + *j + *k < target) {
++j;
while (*j == *(j-1) && j < k) ++j;
} else if (*i + *j + *k > target) {
--k;
while (*k == *(k+1) && j < k) --k;
}else {
result.push_back({*i, *j, *k});
++j;
--k;
while (*k == *(k+1) && *j == *(j-1) && j < k) ++j;
}
}
}
return result;
}
};
以下解法大量使用了容器算法，会触发超时，性能下降
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> result;
sort(nums.begin(), nums.end());
for(auto i = nums.begin(); i < prev(nums.end(), 2); ++i) {
auto j = next(i);
auto k = prev(nums.end(), 1);
while (j < k) {
auto temp = *i + *j + *k;
if(temp > 0) {
--k;
}else if (temp < 0) {
++j;
}else{
result.push_back({*i, *j, *k});
++j;
--k;
}
}
}
sort(result.begin(), result.end());
result.erase(unique(result.begin(), result.end()), result.end());
return result;
}
};
16、最接近的三数之和
最接近的三数之和，其实和三数之和类似，都是要去夹逼去逼近目标，可以进行判断差值是否更小，如果更小，则进行更新；接下来怎么进行遍历，只需要和targer类似三数之和方法进行比较更新即可。
| 对比项 | 三数之和 | 最接近的三数之和 |
|---|---|---|
| 遍历方法 | 左右夹逼 | 左右夹逼 |
| 核心差异 | 1、不能出现相同的数组，且等于目标值时更新时，需要同时更新就j、k | 绝对值差异要求最小，同时更新j、k是不需要的 |
| 输出方式 | 目标数值的集合，可能有多个三数的组合，但不能相同，vector<vector<int>> |
最接近目标的一个数字，int |
class Solution {
public:
int threeSumClosest(vector<int>& nums, int target) {
// 存储结果
int result = 0;
int abs_diff = INT_MAX;
// 其实要求的是接近
sort(nums.begin(), nums.end());
for (auto i = nums.begin(); i < prev(nums.end(), 2); ++i) {
auto j = i + 1;
auto k = prev(nums.end());
// 相同的数字可以直接跳过
if(i > nums.begin() && *i == *(i -1) ) continue;
while(j < k) {
int temp = *i + *j +*k;
if(abs(temp - target) < abs_diff) {
result = temp;
abs_diff = abs(temp - target);
}
if (temp < target) ++j;
else --k;
}
}
return result;
}
};
18、四数之和
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> result;
sort(nums.begin(), nums.end());
for(auto i = nums.begin(); i < prev(nums.end(), 3); ++i) {
for(auto j = next(i); j < prev(nums.end(), 2); ++j) {
auto k = next(j);
auto l = prev(nums.end(), 1);
while (k < l) {
long temp = long(*i) + long(*j) + long(*k) + long(*l);
if (temp < target) {
++k;
}else if (temp > target) {
--l;
}else{
result.push_back({*i, *j, *k, *l});
++k;
--l;
}
}
}
}
sort(result.begin(), result.end());
result.erase(unique(result.begin(), result.end()), result.end());
return result;
}
};
27、移除元素
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int cnt = 0;
// 用cnt来标记长度，即可给cnt赋值即可
for(int i = 0; i < nums.size(); ++i ) {
if (nums[i] != val) {
nums[cnt] = nums[i];
cnt++;
}
}
return cnt;
}
};
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
return distance(nums.begin(), remove(nums.begin(), nums.end(), val));
}
};
31、下一个全排列
#include <vector>
#include <algorithm> // 用于 std::swap 和 std::reverse
class Solution {
public:
void nextPermutation(std::vector<int>& nums) {
auto first = nums.begin(), last = nums.end();
// 找到第一个升序队列
auto i = prev(last);
while(i != first && *(i - 1) >= *i) --i;
if (i != first) {
auto j = prev(last);
while(*j <= *(i-1)) {
--j;
}
iter_swap(i-1, j);
}
reverse(i, last);
}
};
46、全排列
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> result;
do{
result.push_back(nums);
}while(next_permutation(nums.begin(), nums.end()));
return result;
}
};
60、排列序列
方法一：调用多次全排列即可
class Solution {
public:
string getPermutation(int n, int k) {
// 法一调用k次全排列
vector<int> nums;
string result;
for(int i = 1; i <= n; ++i) nums.push_back(i);
for(int i = 0; i < k -1 ; ++i) next_permutation(nums.begin(), nums.end());
for(auto item : nums) result.push_back(to_string(item)[0]);
return result;
}
};
36、有效的数独
class Solution {
public:
bool isValidSudoku(vector<vector<char>>& board) {
// 新建一个数组用于记录3x3矩阵中的数字
bool used[9];
// 检查主体逻辑
for(int i=0; i < 9; ++i) {
// 检查行
fill(used, used+9, false);
for (int j =0; j < 9; ++j) {
if (!check(board[i][j], used)) return false;
}
fill(used, used+9, false);
// 检查列
for (int j =0; j < 9; ++j) {
if (!check(board[j][i], used)) return false;
}
}
// 检查小格子
// 先锁定9宫格，必须有x和y
for (int i =0 ; i < 9; i += 3) {
for (int j =0; j < 9; j += 3) {
fill(used, used+9, false);
for (int h =0; h < 3; ++h) {
for (int k =0; k < 3; ++k) {
if (!check(board[i + h][j + k], used)) return false;
}
}
}
}
return true;
}
// 判断是否不存在
bool check(char c, bool used[9])
{
if (c == '.') return true;
if (used[c - '1']) return false;
return used[c - '1']=true;
}
};
其中有一个陷阱：
每行、每列进行确认是否只能出现一次，for (int j =0; j < 9; ++j)这样是对的，会从每行和每列开始；for (int j =0; j < i; ++j)，这样是错的，会漏掉每行和每列开头的部分
确定小方格时，就不需要确定每行每列是否出现一次，只需要遍历9个元素即可
在C++中， new intn 会将分配的内存初始化为零。这是C++标准中的一个特性，称为“值初始化”（value initialization）。详细解释 new int[n] ：分配一个包含 n 个 int 的数组，但不会初始化数组中的元素。数组中的值将是未定义的（即可能包含任意值）。 new intn ：分配一个包含 n 个 int 的数组，并将所有元素初始化为零。这是因为括号 () 触发了值初始化，对于基本数据类型（如 int ），值初始化会将所有元素设置为零。
42、接雨水
法一：面积计算公式的问题, 动态规划
class Solution {
public:
int trap(vector<int>& height) {
// 思路：每个的柱体的面积是通过左右的min(max[left], max[right])-height决定
// 所以初期要找到左边最大和右边最大
int n = height.size();
int *max_left = new int[n]();
int *max_right = new int[n]();
// 从左到右，从右到左，找寻对应i的最大值
for (int i = 1; i < n; ++i) {
max_left[i] = max(max_left[i-1], height[i-1]);
max_right[n-i-1] = max(max_right[n-i], height[n-i]);
}
int sum = 0;
for (int i =0; i< n; ++i) {
int A = min(max_left[i], max_right[i]);
if (A > height[i]) {
sum += A - height[i];
}
}
delete[] max_left;
delete[] max_right;
return sum;
}
};
法二
单调栈
class Solution {
public:
int trap(vector<int>& height) {
vector<int> numsStack;
int waterCount = 0;
for (int i = 0; i < height.size(); ++i){
while (!numsStack.empty() && height[numsStack.back()] < height[i]){
int top = numsStack.back();
numsStack.pop_back();
if (numsStack.empty()){
break;
}
int left = numsStack.back();
int w = i - left -1;
int h = min(height[left], height[i]) - height[top];
waterCount += h * w;
}
numsStack.push_back(i);
}
return waterCount;
}
};
法三：双指针法
1、将雨水图对半分，分别计算左边和右边的能接雨水的面积，从左右开始同时算
2、然后根据左右半区的最大值更小的一个值确定哪边该就接雨水
class Solution {
public:
int trap(vector<int>& height) {
int ans = 0;
int left = 0, right = height.size() - 1;
int leftMax = 0, rightMax = 0;
while (left < right) {
leftMax = max(leftMax, height[left]);
rightMax = max(rightMax, height[right]);
if (height[left] < height[right]) {
ans += leftMax - height[left];
++left;
} else {
ans += rightMax - height[right];
--right;
}
}
return ans;
}
};
48、旋转图像
首先从外到内进行遍历是很浪费时间的，直接先转置再翻转是最快的
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
// 矩阵转置 + 矩阵翻转
int n = matrix.size();
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
swap(matrix[i][j], matrix[j][i]);
}
}
for (int i = 0; i < n; i++) {
reverse(matrix[i].begin(), matrix[i].end());
}
}
};
浙公网安备 33010602011771号