三维逆向运动学

本文将教您如何掌握三维逆向运动学，可以解决如何移动机械臂以到达特定目标的问题。

您可以通过下方链接查阅前置的技术知识分享：

可以在本文末尾找到下载整个 Unity 包的链接。

 

介绍

逆向运动学。毫无疑问是机器运动控制领域中提及最多的课题，关于电子游戏背景下的逆向运动学，有许多知识要研究学习和慢慢分享。

是什么让逆向运动学如此复杂但有趣，以至于需要这么深入展开研究和分享？事实是，逆向运动学是一个不仅在视频游戏中而且在工程和科学中都反复出现的课题。从机械臂的设计到对人脑运动控制的理解，逆向运动学（以一种或多种形式）发挥着重要作用。

简要总结

2017 年，第一个专门讨论该主题的系列《程序动画简介》问世，进一步在独立开发者中普及了“程序动画”一词。它提供了一个基于梯度下降算法的通用解决方案，该算法可能用于相当“奇特”的传动装置，例如触手和蜘蛛腿。

第二个系列《二维逆向运动学》在一年后问世，重点关注一个非常具体的情况：一个被约束在二维平面上的双关节臂（如下图）。顾名思义：二维逆运动学的两个关节中的每一个都由一个角度控制，一个和B。通过调制这两个角度，机械臂的尖端（称为末端执行器）将到达不同的位置。

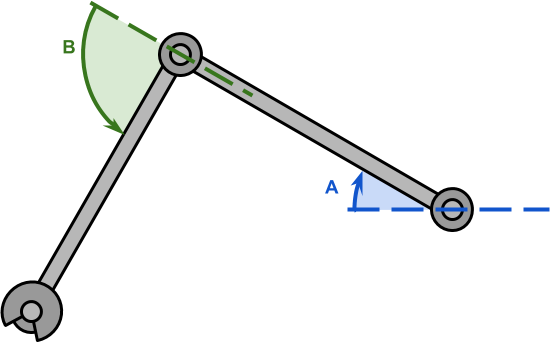
逆向运动学的问题是找到角度一个，B使末端执行器达到所需的目标点。下面的动画显示了一个机械臂，它正在绘制一个圆，在 XY 平面上对齐。

从技术上讲，机械臂逆向运动学提出的解决方案可以处理任意数量的关节。那么，为什么要专注于功能较弱的技术呢？答案很简单：效率。值得一提的是，在刚才描述的特定场景中，可以使用简单的方程而不是相当复杂的算法找到解决方案。我们可以将机械臂想象成一个具有两个内角\阿尔法和\试用版三角形（下图）。

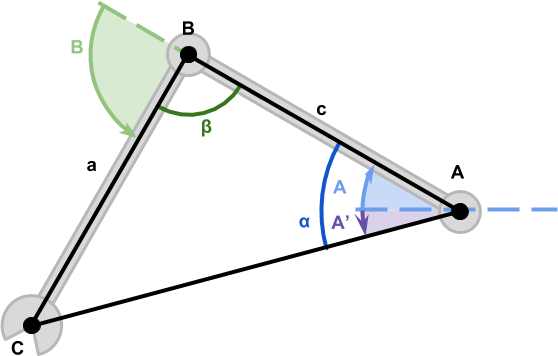
通过一些三角函数公式，我们发现这些角度的值为：

(1) \begin{equation*} \alpha = \cos^{-1}{\left（\frac{b^2+c^2-a^2}{2bc}\right）} \end{equation*}

(2) \begin{equation*} \beta=\cos^{-1}{\left（\frac{a^2 + c^2 -b^2}{2ac}\right）} \end{equation*}

其中 一个，b和c是我们构造的这个“假想”三角形的边。

机械臂的关节是使用 一个 和 B控制的，结果是：

(3) \begin{方程*} A = \alpha + A' \end{方程*}

(4) \begin{方程*} B = \pi - \beta \end{方程*}

那么：

(5) \begin{equation*} A' = \tan^{-1}{\left（\frac{C_Y-A_Y}{C_X-A_X}\right）} \end{equation*}

📚我们看看推导过程 
完整的推导可以在标题为“二维逆向运动学：数学”的文章中找到。

延伸到第三维度

如果您之前关注过 二维逆向运动学：数学和二维逆向运动学：代码，那么相比之前不会有任何新内容。如果你还没有，不要担心，这就是你需要知道的。

这个简化的情况之所以值得讨论，是因为它可以用作求解 三维逆向运动学的起点。

首先，我们需要了解二维逆向运动中双关节臂的场景是具有两个自由度 （2DOF） 的问题。与人们想象的相反，这并不意味着我们有两个部分;但是我们可以控制两个变量（在这种情况下，结果是关节角）。

当我们把这个问题扩展到第三维时，我们的机械臂仍然有两个部分和两个关节。然而，如果我们假设我们也可以围绕它的第一个关节自由旋转手臂，那么问题现在有三个自由度 （3DOF）。

在这种新方案下，第二个关节（B）保持不变。但是，我们假设第一个（一个）现在可以在另一个维度上自由旋转。因此，第一个关节通常被称为髋关节，第二个关节被称为膝盖。您的膝盖通常只有一个自由度（向前/向后），而您的髋关节有两个自由度（向前/向后和向内/向外）。髋关节旋转的角度用 \西塔表示。

我们可以想象一个机械臂，其中两个关节可以有两个自由度，总共四个。此时的问题是，将有多种解决方案，使我们的方法不再有效。“腿状”机械臂（意思是：具有髋关节和膝关节的手臂）在游戏和整个行业中都非常普遍。所以这种方法可能值得研究。

如果您已经阅读了之前的文章，您可能还记得，如果目标在 2D 中是可到达的，则始终有两种“镜面反射”解决方案（如下）。

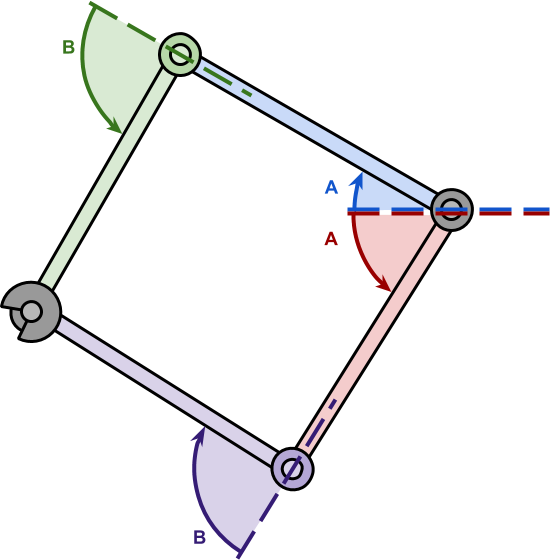
同样的问题也发生在 3D 中;这一次，解决方案是无限的。这是因为配置可以围绕连接原点和目标的直线表示的对称轴旋转。解决方案是...只专注于一个解决方案！在本文中，我们将重点介绍最容易找到的方向，它假设 （0， 1， 0） 作为“向上”方向。

从2D到3D

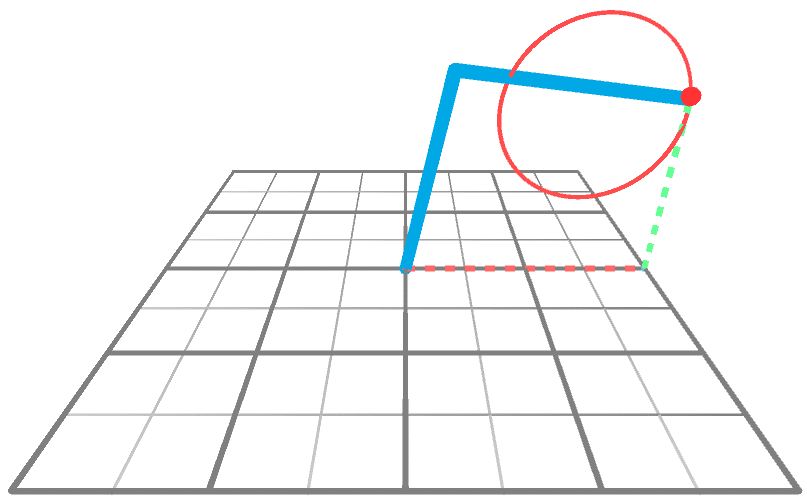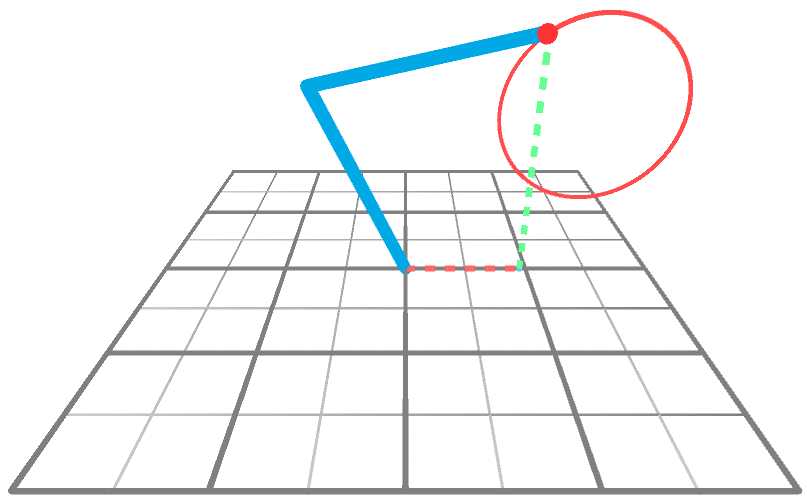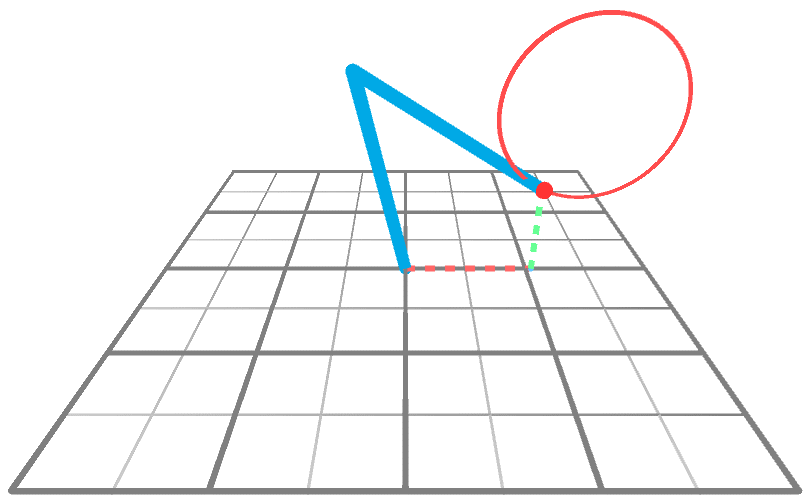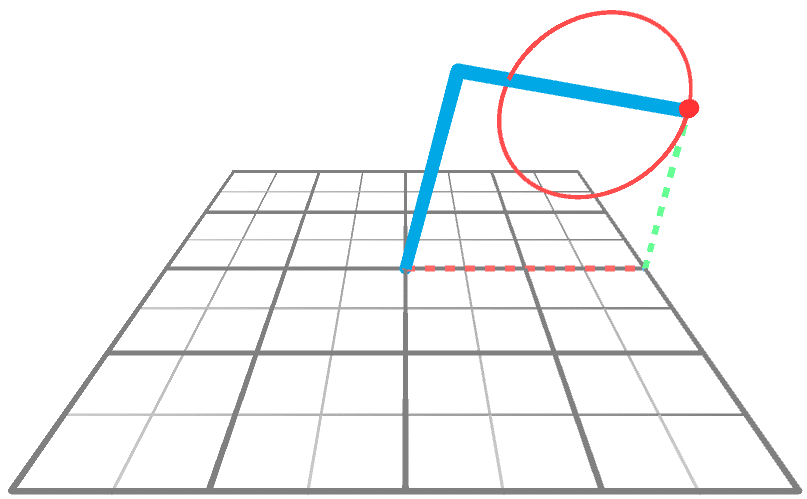
到目前为止，我们只知道如何解决运动对 XY 平面的约束时的反运动学问题。从 2D 到 3D 的诀窍是重用 2D 解决方案。下面的动画显示了一个机械臂伸向 3D 空间中的一个点，该点围绕 Y 轴旋转。很明显，手臂唯一要做的就是旋转;它的角度一个没有B改变，只是\西塔改变。

这意味着，如果我们知道如何在 XY 平面上执行 IK（我们确实知道！），我们就知道如何通过两次简单的旋转在整个 XYZ 空间上执行它。从概念上讲，我们可以通过三个步骤解决问题：

  1. 绕 Y 轴旋转目标点，直到它位于 XY 平面上
  2. 移动机械臂，使其能够触及该点，就好像它是在 2D 中一样
  3. 通过在 Y 轴上沿相反方向旋转整个机械臂来“撤消”旋转。

我们可以通过简单地执行 2D 逆向运动学来更有效地做到这一点，而不是在 XY 平面上，而是在从机械臂根部传递到目标点的垂直平面上。

绕 Y 轴旋转

要在 3D 中执行逆向运动学，我们首先需要计算的是 \西塔，这是整个机械臂围绕的角度旋转。这是髋关节增加的额外自由度。

找到它的最佳方法是假设机械臂已经到达该位置（意味着C已经在目标位置）并计算结果角度\西塔。由于\西塔是髋关节围绕 Y 轴形成的角度，我们可以直接从顶部查看机械臂。从XZ平面（下图）的自上而下视图来看，机械臂看起来像一条直线。这是因为，除了髋关节之外，其他两个关节都是平面上的约束。

如果我们把线段\overline{AC}看作是直角三角形的斜线，我们可以使用一点三角函数来计算角度\西塔：

(6) \begin{equation*} \theta = \tan^{-1}{\left（\frac{\Delta z}{\Delta x}\right）} = \tan^{-1}{\left（\frac{C_Z-C_Z}{C_X-A_X}\right）} \end{equation*}

📚给我看看推导！
计算两点之间的角度对于游戏开发者来说是一个非常普遍的问题，可以通过一点三角函数轻松解决。

 

在这种情况下，诀窍是引入一条线的斜率（如下图），即其上升 （\Delta y） 和运行 （\Delta x） 之间的比率。可以在任意两个给定的不同点之间计算一条线的斜率，并产生相同的结果。

一条线的斜率与线\gamam的角度有直接关系：

(7) \begin{equation*} \frac{\Delta y}{\Delta x} = \tan{\gamma} \end{equation*}

如果你学过三角学，你实际上应该认识到上升\Delta y是事实\sin{\gamma}，运行\Delta x是 \cos{\gamma}。根据定义，切函数是正弦和余弦之间的比值。

为了\gamma从（7）中提取，我们可以使用反正切函数，称为反正切：

(8) \begin{equation*} \gamma = \tan^{-1}{\left（\frac{\Delta y}{\Delta x}\right）} \end{equation*}

虽然这在理论上效果很好，\Delta x但 和 \Delta y的符号存在一些问题。事实上，当 和 \Delta y 都为正或均为负时\Delta x，斜率会产生相同的结果。但是，从几何的角度来看，它们对应于两个相反的角度！解决办法是不要直接使用，而是它的\tan^{-1}“编程”表亲，

arctan2
.大多数框架都有反正切函数的实现，该函数采用两个参数，通常称为 Dy 和
Dx
.

 

 

⭐建议的 Unity 资源⭐
 
 
Unity是免费的，但您可以升级到Unity Pro或Unity Plus订阅计划，以获得更多功能和培训资源，以增强您的项目。

 

WY平面上的反向运动学

从技术上讲，知道\西塔足以解决 3D 中的逆运动学问题。事实上，我们可以做的是遵循上一节中介绍的算法：绕 Y 轴将目标点旋转-\西塔度数，在 XY 平面上执行逆运动学，最后将整个臂旋转+\θ度数。

更快的方法是不是在 2D 平面上执行逆向运动学，而是直接在通过髋关节和目标点的垂直平面上执行。不幸的是，有些东西阻止了我们这样做。让我们再看一遍图表，它指示了所有使用的角度：

为了计算 一个，这是控制第一个关节的角度，我们需要计算A'。即第一个关节与目标点之间的角度，如果我们回想一下用于计算A'的方程（5），我们会注意到一个大问题：它假设所有点都位于XY平面上：

  \begin{equation*} A' = \tan^{-1}{\left（\frac{C_Y-A_Y}{C_X-A_X}\right）} \end{equation}

不幸的是，在我们的 3D 场景中，机械臂将围绕 Y 轴旋转\西塔度数。但是，如果我们将视图与机械臂一起旋转，则新图基本保持不变。我们称这个新的参考系为 WY，因为 X 轴现在被 W 取代，W 是 X 轴，而不是绕 Y 轴旋转\西塔度数。

我们不能简单地像D_X-A_X我们所做的那样\Delta y。这是因为 while C 和 D 在 Y 轴上对齐， 一个 D而不与 X 轴对齐。它们与 W 轴对齐。因此，最好的计算\Delta w方法是获得从 一个 到 D的距离。这失去了 \Delta w的符号，但幸运的是，它对我们的计算没有真正的问题。如果您的手臂碰巧向相反方向移动，只需翻转代码\Delta w中的符号即可。

(9) \begin{equation*} A' = \tan^{-1}{\left（\frac{\Delta y}{\Delta w}\right）} =\tan^{-1}{\left（\frac{C_Y-D_Y}{\left|\overline{A D}\right|}\right）} \end{方程*}

其中\left|\overline{A D}\right|，是从 一个 到 D的段的长度。它可以通过以下函数轻松计算

向量3。距离
，或者你也可以直接使用毕达哥拉斯定理：

 

(10) \begin{equation*} \begin{align} A' &=& \tan^{-1}{\left（\frac{C_Y-D_Y}{ \sqrt{\left（C_X - A_X\right）^2+\left（A_Y- A_Y\right）^2+\left（C_Z - A_Z\right）^2 }\right）}} = \\ &=& \tan^{-1}{\left（\frac{C_Y-D_Y}{ \sqrt{\left（C_X - A_X\right）^2+\left（C_Z - A_Z\right）^2 }\right）}} \end{align} \end{equation*}

 

在上面的方程中，毕达哥拉斯定理的 Y 贡献会自行抵消，因为该点D具有相同的 Y 分量一个，因此它们的\Delta y分量为零。

现在，我们确实拥有了在3D中对具有一个敏锐和髋关节的机械臂进行逆向运动学的一切：

(11) \begin{equation*} \theta = \tan^{-1}{\left（\frac{C_Z-C_Z}{C_X-A_X}\right）} \end{equation*}

(12) \begin{equation*} A = \cos^{-1}{\left（\frac{b^2+c^2-a^2}{2bc}\right）} + \tan^{-1} { \left（ \frac {C_Y-D_Y} { \sqrt { \left（C_X - A_X\right）^2 +\left（C_Z - A_Z\right）^2 } } \right）} \end{equation*}

(13) \begin{equation*} B &=& \pi - \cos^{-1}{\left（\frac{a^2 + c^2 -b^2}{2ac}\right）} \end{equation*}

虽然看起来很吓人，但这些方程很容易实现，并且可以尽可能快地在 3D 中执行反向运动学。

下一步...

本系列的下一个教程将展示如何使用反向运动学来创建可信的有腿生物。是的，关于蜘蛛腿逆运动学的预期教程终于来了!!

📚给我看看推导！
计算两点之间的角度对于游戏开发者来说是一个非常普遍的问题，可以通过一点三角函数轻松解决。

 

在这种情况下，诀窍是引入一条线的斜率（如下图），即其上升 （\Delta y） 和运行 （\Delta x） 之间的比率。可以在任意两个给定的不同点之间计算一条线的斜率，并产生相同的结果。

一条线的斜率与线\gamam的角度有直接关系：

(7) \begin{equation*} \frac{\Delta y}{\Delta x} = \tan{\gamma} \end{equation*}

如果你学过三角学，你实际上应该认识到上升\Delta y是事实\sin{\gamma}，运行\Delta x是 \cos{\gamma}。根据定义，切函数是正弦和余弦之间的比值。

为了\gamma从（7）中提取，我们可以使用反正切函数，称为反正切：

(8) \begin{equation*} \gamma = \tan^{-1}{\left（\frac{\Delta y}{\Delta x}\right）} \end{equation*}

虽然这在理论上效果很好，\Delta x但 和 \Delta y的符号存在一些问题。事实上，当 和 \Delta y 都为正或均为负时\Delta x，斜率会产生相同的结果。但是，从几何的角度来看，它们对应于两个相反的角度！解决办法是不要直接使用，而是它的\tan^{-1}“编程”表亲，

arctan2
.大多数框架都有反正切函数的实现，该函数采用两个参数，通常称为
dy
和
dx
.

 

 

⭐建议的 Unity 资源⭐
 
 
Unity是免费的，但您可以升级到Unity Pro或Unity Plus订阅计划，以获得更多功能和培训资源，以增强您的项目。

 

WY平面上的反向运动学

从技术上讲，知道\西塔足以解决 3D 中的逆运动学问题。事实上，我们可以做的是遵循上一节中介绍的算法：绕 Y 轴将目标点旋转-\西塔度数，在 XY 平面上执行逆运动学，最后将整个臂旋转+\θ度数。

更快的方法是不是在 2D 平面上执行逆向运动学，而是直接在通过髋关节和目标点的垂直平面上执行。不幸的是，有些东西阻止了我们这样做。让我们再看一遍图表，它指示了所有使用的角度：

为了计算 一个，这是控制第一个关节的角度，我们需要计算A'。即第一个关节与目标点之间的角度，如果我们回想一下用于计算A'的方程（5），我们会注意到一个大问题：它假设所有点都位于XY平面上：

  \begin{equation*} A' = \tan^{-1}{\left（\frac{C_Y-A_Y}{C_X-A_X}\right）} \end{equation}

不幸的是，在我们的 3D 场景中，机械臂将围绕 Y 轴旋转\西塔度数。但是，如果我们将视图与机械臂一起旋转，则新图基本保持不变。我们称这个新的参考系为 WY，因为 X 轴现在被 W 取代，W 是 X 轴，而不是绕 Y 轴旋转\西塔度数。

我们不能简单地像D_X-A_X我们所做的那样\Delta y。这是因为 while C 和 D 在 Y 轴上对齐， 一个 D而不与 X 轴对齐。它们与 W 轴对齐。因此，最好的计算\Delta w方法是获得从 一个 到 D的距离。这失去了 \Delta w的符号，但幸运的是，它对我们的计算没有真正的问题。如果您的手臂碰巧向相反方向移动，只需翻转代码\Delta w中的符号即可。

(9) \begin{equation*} A' = \tan^{-1}{\left（\frac{\Delta y}{\Delta w}\right）} =\tan^{-1}{\left（\frac{C_Y-D_Y}{\left|\overline{A D}\right|}\right）} \end{方程*}

其中\left|\overline{A D}\right|，是从 一个 到 D的段的长度。它可以通过以下函数轻松计算

向量3。距离
，或者你也可以直接使用毕达哥拉斯定理：

 

(10) \begin{equation*} \begin{align} A' &=& \tan^{-1}{\left（\frac{C_Y-D_Y}{ \sqrt{\left（C_X - A_X\right）^2+\left（A_Y- A_Y\right）^2+\left（C_Z - A_Z\right）^2 }\right）}} = \\ &=& \tan^{-1}{\left（\frac{C_Y-D_Y}{ \sqrt{\left（C_X - A_X\right）^2+\left（C_Z - A_Z\right）^2 }\right）}} \end{align} \end{equation*}

 

在上面的方程中，毕达哥拉斯定理的 Y 贡献会自行抵消，因为该点D具有相同的 Y 分量一个，因此它们的\Delta y分量为零。

现在，我们确实拥有了在3D中对具有一个敏锐和髋关节的机械臂进行逆向运动学的一切：

(11) \begin{equation*} \theta = \tan^{-1}{\left（\frac{C_Z-C_Z}{C_X-A_X}\right）} \end{equation*}

(12) \begin{equation*} A = \cos^{-1}{\left（\frac{b^2+c^2-a^2}{2bc}\right）} + \tan^{-1} { \left（ \frac {C_Y-D_Y} { \sqrt { \left（C_X - A_X\right）^2 +\left（C_Z - A_Z\right）^2 } } \right）} \end{equation*}

(13) \begin{equation*} B &=& \pi - \cos^{-1}{\left（\frac{a^2 + c^2 -b^2}{2ac}\right）} \end{equation*}

虽然看起来很吓人，但这些方程很容易实现，并且可以尽可能快地在 3D 中执行反向运动学。

下一步...

本系列的下一个教程将展示如何使用反向运动学来创建可信的有腿生物。是的，关于蜘蛛腿逆运动学的预期教程终于来了!!

posted @ 2024-03-18 09:58  soliang  阅读(85)  评论(1)  编辑  收藏  举报