快速傅里叶变换 FFT 学习笔记
FFT ( 快速傅里叶变换 ) 学习笔记
本文有错误之处请诸位大佬多多指正!
\(FFT\) :快速傅里叶变换的英文缩写,快速傅里叶变换是对离散傅里叶变换 \(DFT\) 的优化,用来解决多项式上的操作如 卷积 等问题。
参考文章:
https://www.luogu.com.cn/blog/command-block/fft-xue-xi-bi-ji
https://blog.csdn.net/weixin_43346722/article/details/116353343
https://www.cnblogs.com/zwfymqz/p/8244902.html
多项式
系数表示法
一般在 初中 数学上,表示一个多项式我们用的是系数表示法
设 \(A(x)\) 表示一个关于\(x\) 的 \(n\) 次的多项式,那么:
展开后就是:
然后两个多项式相乘,每一项都要和另一个多项式的每一项相乘,时间复杂度\(O(n^2)\)
点值表示法
我们找 \(n+1\) 组不同的 \(x\) 代入多项式,就可以得出 \(n+1\) 个 \(y\) 值,
我们把它们对应:\((x_0,y_0),(x_1,y_1)······(x_n,y_n)\)
其中 \(y_i=\sum\limits_{j=0}^{n-1}a_j*x_i^j\)
听说这玩意叫做 \(DFT\),怎么和我的名字缩写一样
当然,你会发现时间复杂度还是没有变化,选点 \(O(n)\),计算 \(O(n)\),总共 \(O(n^2)\)
然后好像没有啥卵用
最后你可悲的发现,好像时间复杂度在\(O(n^2)\)处达到了下限,没有什么优化的空间。
但是数学家们的智慧不是你能揣测的。
前方第一波高能!!!
复数
前置芝士
向量
具有大小又有方向的量,在物理上又称矢量,比如说力,加速度等都是向量。
在图上一般用一根箭头来表示。
弧度制
\(1~^∘=\frac {\pi}{180}~~rad\)
\(180~^∘=1~~\pi~~rad\)
定义
我们设 \(a,b\in R\),\(i^2=-1\),所有形如 \(a+bi\) 的数通称为复数,其中 \(i\) 被称为虚数单位,\(bi\) 被称为复数的虚部,\(a\) 被称为实部,如果一个复数只有 \(bi\) 部分,那么这个复数被称为纯虚数。
复数域 \(C\) 是目前最大的域,实数集是复数集的真子集。
如何表示复数?
我们建立一个平面直角坐标系,称之为复平面, \(x\) 轴代表实轴,\(y\) 轴代表虚轴 (除原点外),那么 \(x\) 轴上的点表示的就是实数(类比数轴),\(y\) 轴除原点外表示的都是纯虚数,原点表示实数 \(0\) 。那么对于每一个复数 \(a+bi\),我们都可以用复平面上的点 \((a,b)\) 来表示这个复数,或者我们可以看做是起点为 \((0,0)\) 终点为 \((a,b)\) 的向量。
复数的模长:就是向量的大小,具体来说就是\(\sqrt {a^2+b^2}\)
幅角:假以逆时针为正方向,从 \(x\) 轴正半轴到已知向量的转角的有向角叫做幅角.
运算法则
加法遵循向量的平行四边形法则,这个玩意长这样:(盗的别人的图)

\(\vec{AB}+\vec{BC}=\vec{AD}+\vec{DC}=\vec{AC}\)
减法:加法的时候将向量变成反过来的(终点变起点,起点变终点)
乘法:
几何定义:模长相乘,幅角相加(虽然我也不懂)
证明:
对于每一个复数,都可以表示成\(r(\cos x+i*\sin x )\) 的形式,其中 \(r\) 为复数的模长,\(x\) 是幅角 (不理解的建议学学三角函数 勾股定理 )
对于两个复数 \(r_1(\cos x+i*\sin x )~,~r_2(\cos y+i*\sin y )\)
相乘,得到的答案: ( \(i^2=-1\) 所以第二项变成了减号 )
根据三角恒等变换式 (不会的翻翻高中数学必修第一册最后一章)
\(\cos(x+y)=\cos x\cos y-\sin x\sin y~~,~~\sin(x+y)=\sin x\cos y+\sin y\cos x\)
再看看上面的式子,我们发现可以化简:
所以就有了模长相乘 (显然),幅角相加 (还是显然)
代数定义:
因为\(i^2=-1\) ,就有$$(ac-bd)+(ad+bc)i$$
搞定。
然后你会一头雾水的发现,这和多项式乘法有什么关系啊?
别急,真正的好东西来了。
单位根
注:以下提到的复数都是在单位圆上的复数。
在复平面上,以原点为圆心,\(1\) 为半径作圆,所得的圆叫单位圆。
又去盗了一张图
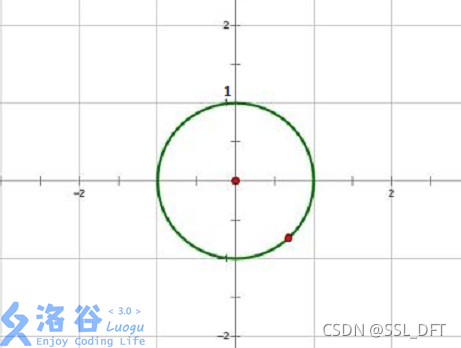
以圆点为起点,圆的 \(n\) 等分点为终点,做\(n\)个向量,设幅角为正且最小的向量对应的复数为 \(ω_n^1\),称为 \(n\) 次单位根。
就是 \(x^n=1\) 在复数域上的 \(n\) 个解
根据复数乘法的运算,其余 \(n−1\) 个复数为\(ω^2_n,ω^3_n,…,ω^n_n\)
其中\(\omega^0_n=\omega_n^n=1\)(对应在 \(x\) 轴上长度为 \(1\) 的向量)
然后我们就有$$\omega^k_n=\cos k~\frac{2\pi}{n}+i*\sin k~\frac{2\pi}{n}$$
单位根的几条性质:
\((1):~~~~\omega_n^k=(\omega_n^1)^k\)
证明:两个向量相乘,模长相乘还是 1 ,幅角相加,总共加了 \(k\) 次 (也可以看做向逆时针方向旋转了 \(\frac{k}{n}\) 个圆周),所以就是\(\omega_n^k\) (显而易见)
(2):\(\omega_n^i*\omega_n^j=\omega_n^{i+j}\)
证明:\(\omega_n^i=(\omega_n^1)^i~,~\omega_n^j=(\omega_n^1)^j~,~\omega_n^i*\omega_n^j=(\omega_n^1)^i*(\omega_n^1)^j=(\omega_n^1)^{i+j}=\omega_n^{i+j}\)
(3):\(\omega_n^k=\omega_{pn}^{pk}\)
证明:把 \(\omega_{pn}^{pk}\) 这玩意代入到单位根的表示的式子里,发现分子分母同时乘了一个 \(p\) ,复数的值不变
(4):\(\omega_n^{k+\frac{n}{2}}=-\omega_n^k\)
证明:\(\omega_n^\frac{n}{2}=\cos \frac{n}{2}·\frac{2\pi}{n}+i*\sin \frac{n}{2}·\frac{2\pi}{n}=\cos\pi+i*\sin\pi\)
众所周知 根据三角函数表,其中 \(\cos\pi=-1~,~\sin\pi=0\)
所以\(\omega_n^\frac{n}{2}=-1~,~\omega_n^{k+\frac{n}{2}}=\omega_n^k*\omega_n^{\frac{n}{2}}=-\omega_n^k\)
当然你可以看做把这个复数向逆时针方向旋转了\(\frac{n}{2}\) 个圆周 (就是一个半圆),然后这个新的复数和之前的复数就关于原点对称了 (建议画图理解)
(5):\(\omega_n^k~(k\geq n)=\omega_n^{k\bmod n}\)
证明:很明显这个复数围绕单位圆转了 \(\frac{n}{n}=1\) 圈后回到了之前的位置,对答案没有影响。
用三角函数的角度来理解就是终边相同的角三角函数值相等
正文真正的开始
快速傅里叶变换:
前文说到,对于一个 \(n\) 次多项式,我们可以用 \(n+1\) 个点来确定
对于一个 \(n-1\) 次多项式 \(A(x)\),我们的超级神仙傅里叶 降下了一道救世之光,拯救了那些被多项式梦魇诅咒的善良之人 反手将这个多项式拍成了渣渣,然后按照奇偶性分成了两半,就有了这个东西:
这时候我们设
对应上面把\(A(x)\)切成两半的操作,我们 惊悚 惊喜地发现:
这时候我们把\(\omega_n^k\) ( \(k\leq \frac{n}{2}\) ) 代入这个式子:
然后再把\(\omega_n^{k+\frac{n}{2}}\) 代入,得到:
再根据 \(\omega_n^{k+\frac{n}{2}}=-\omega_n^k\),得到
我们惊喜的发现,两个式子只有一个常数项不同,那么你每一次枚举一个式子的时候,你可以在 \(O(1)\) 时间复杂度之内求出第二个式子的值,那么你的问题就缩小了一半!这时候你还会发现,对于第一个式子,继续拆分,它的问题规模又可以减半,那就可以递归实现了 (是不是很玄学)
不要以为这样就结束了,逼事还有一大堆呢
快速傅里叶逆变换 (IFFT):
当你以为你搞定了前面的东西的时候,你发现你得到的是一堆点值表达式,好像并没有卵用
你悲哀的发现你只会系数表示法, 点值表示法你不会······
所以你就必须将这个点值表示法的多项式转换为系数表示法来表示。
所以神仙数学家们又搞了一个叫做快速傅里叶逆变换 ( \(IFFT\) ) 的东西。
内容:
我们设\((y_0,y_1,y_2···y_{n-1})\) 为多项式\((a_0,a_1,a_2···a_{n-1})\) 的傅里叶变换
这时候我们再设 \((c_0,c_1,c_2···c_{n-1})\) 是 \((y_0,y_1,y_2···y_{n-1})\) 在 \(\omega_n^0,\omega_n^{-1}···,\omega_n^{-(n-1)}\) 处的傅里叶变换
那么就有 \(c_k=\sum\limits_{i=0}^{n-1}y_i*(\omega_n^{-k})^i\)
推式子高能警告!!!
展开式子:
注意 \(j,i\) 位置的调换
这时候我们设 \(S(x)=\sum\limits_{i=0}^{n-1}x_i\)
代入 \(\omega_n^k\) ,有
当 \(k!=0\) 时,这时候 \(\omega_n^k~!=1\)
将这个式子乘上 \(\omega_n^k\) ,就有了:
后式减去前式,得到:
因为 \(\omega_n^n=1\),所以这个分数的分子为 \(0\),分数值为 \(0\)
当 \(k=0\) 的时候,\(S(\omega_n^k)=1+1+1+·····=n\)
这时候我们看回刚刚这个式子:
当 \(j-k~!=0\) 时,贡献为 \(0\)
当\(j=k,j-k=0\) 时,贡献为 \(n\)
所以就有 \(c_k=n*a_k\)
最后$$a_k=\frac{c_k}{n}$$
这样我们就得到了点值表示法和系数表示法之间的关系啦。
这个过程和上一个过程一样,都可以分治递归来实现
迭代优化
你慢悠悠的打出了一个递归,交上洛谷,然后只有 \(77\) 分
没错,递归常数太大,在 \(10^6\) 的常数面前,它没了······ (但这并不表示这个算法是不可行的)
所以我们把递归扔掉,使用迭代
去盗了一个大佬的图
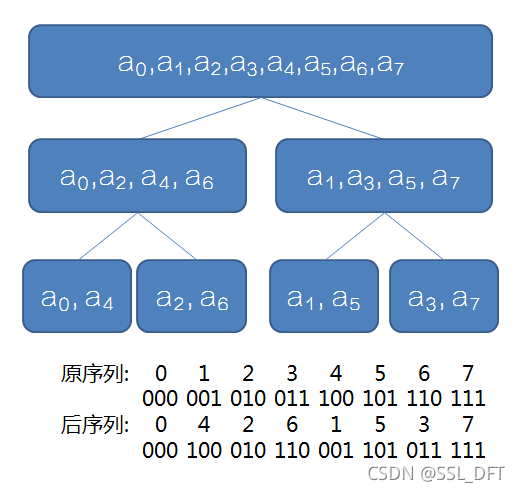
有没有看出什么显而易见的性质?
没错,我们需要求的序列实际是原序列下标的二进制反转 (真的玄学)
因此没有必要对数列的奇偶性进行分类
然后我就不会证了
来看看这位 command_block 大佬的博客
原文地址:https://www.luogu.com.cn/blog/command-block/fft-xue-xi-bi-ji
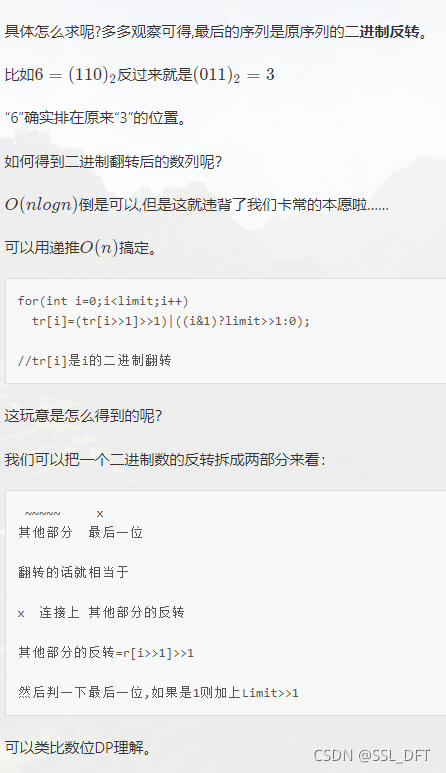
最后迭代就是从下往上合并
悄悄话
累死我了,终于打完了······
(热泪盈眶)
代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#include<cmath>
#define r register
#define rep(i,x,y) for(r ll i=x;i<=y;++i)
#define per(i,x,y) for(r ll i=x;i>=y;--i)
using namespace std;
typedef long long ll;
const ll V=(1e7+10)/2;
const double pi=acos(-1.0);
ll in()
{
ll res=0,f=1;
char ch;
while((ch=getchar())<'0'||ch>'9')
if(ch=='-') f=-1;
res=res*10+ch-48;
while((ch=getchar())>='0'&&ch<='9')
res=res*10+ch-48;
return res*f;
}
ll n,m,f[V];
ll now,k;
struct complex
{
double x,y;
complex (double xx=0,double yy=0) { x=xx,y=yy; }
}a[V],b[V];
complex operator + (complex a,complex b) { return complex(a.x+b.x,a.y+b.y); }
complex operator - (complex a,complex b) { return complex(a.x-b.x,a.y-b.y); }
complex operator * (complex a,complex b) { return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x); }
void FFT(complex *a,ll v)
{
rep(i,0,now-1)
if(i<f[i]) swap(a[i],a[f[i]]);
for(r ll mid=1;mid<now;mid<<=1)
{
complex Wn(cos(pi/mid),v*sin(pi/mid));
ll R=mid<<1;
for(r ll j=0;j<now;j+=R)
{
complex val(1,0);
for(r ll k=0;k<mid;++k,val=val*Wn)
{
complex x=a[j+k],y=val*a[j+mid+k];
a[j+k]=x+y;
a[j+mid+k]=x-y;
}
}
}
}
int main()
{
scanf("%lld%lld",&n,&m);
rep(i,0,n) a[i].x=in();
rep(i,0,m) b[i].x=in();
now=1;//单位根中的k值,默认为2的自然数次幂
while(now<=n+m) now<<=1,++k;
rep(i,0,now-1)
f[i]=(f[i>>1]>>1)|((i&1)<<(k-1));
FFT(a,1);
FFT(b,1);
rep(i,0,now) a[i]=a[i]*b[i];
FFT(a,-1);
rep(i,0,m+n)
printf("%lld ",(ll)(a[i].x/now+0.49));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号