基于风险的完整性和检查建模(RBIIM)MATLAB仿真

1.程序功能描述
基于风险的完整性和检查建模(Risk-Based Integrity and Inspection Modeling ,RBIIM)MATLAB仿真，对比prior density，posterior perfect inspection，posterior imp inpection，cummulative posterior imperfect inspection四个指标。

2.测试软件版本以及运行结果展示
MATLAB2022A版本运行

 

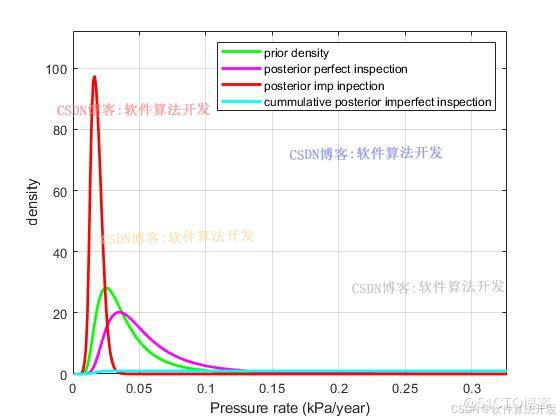
（完整程序运行后无水印）

3.核心程序

function likeliprod = likelihoods(x, t, d, L, n)
 
% 初始化变量
N        = length(x);          % x向量的长度
K        = length(t);          % t向量的长度
N1       = 10000;              % 似然函数中的常数
vc       = 0.5;                % 变量vc
D        = 4.45;               % 变量D
 
% 初始化矩阵存储每个观测值和参数组合的似然值
likelihood = zeros(N, K);
likeliprod = zeros(N, 1);
 
% 下面的思路是在原论文的似然函数基础上，加入带有n的功能，为了区分，将原来公式中的n改写为N1。
for j = 1:N
    % 输出当前循环的索引j（可选，实际应用中可以去掉）
    j
    
    for k = 1:K
        % 根据n(j)的值更新d(j)
        if n(j) == 1
            d(j) = d(j);         % 如果n(j)为1，则不改变d(j)
        else
            d(j) = 5.39 + 0.19*d(j) - 0.02*L(j) + n(j);  % 否则按照公式更新d(j)
        end
        
        % 计算单个观测值x(j)和参数t(k)对应的似然值
        likelihood(j, k) = (1 / N1) * sum(exp(- (t(k) / vc^2) * log(x(j) * vc^2) ...
                                             - gammaln(t(k) / vc^2) + ...
                                             (t(k) / vc^2 - 1) * log(D(k) - min(D(k) - 0.001, d(:, k))) ...
                                             - (D(k) - min(D(k), d(:, k))) / (x(j) * vc^2)));
    end
end
 
% 计算所有参数组合的似然值乘积
likeliprod = prod(likelihood, 2);

　　

4.本算法原理
基于风险的完整性和检查建模 (Risk-Based Integrity and Inspection Modeling, RBIIM) 是一种综合的方法，用于评估和优化资产的完整性管理计划，特别是针对石油化工、能源和其他关键基础设施中的管道、储罐和其他压力容器。这种方法利用了贝叶斯统计框架来更新对资产健康状况的估计，并基于这些估计来制定最佳的维护和检查策略。

4.1 Prior Density (先验密度)
在贝叶斯统计中，先验密度p(θ) 表示在获得任何新观测数据之前，对于未知参数θ 的概率分布。这个分布反映了我们对 θ 的初始信念或知识。例如，在RBIIM中，θ 可能代表管道壁厚的退化程度或腐蚀速率等参数。

 

4.5 举例说明