基于遗传优化算法的TSP问题求解matlab仿真

1.程序功能描述
基于遗传优化算法的TSP问题求解，分别对四个不同的城市坐标进行路径搜索。

2.测试软件版本以及运行结果展示
MATLAB2022A版本运行

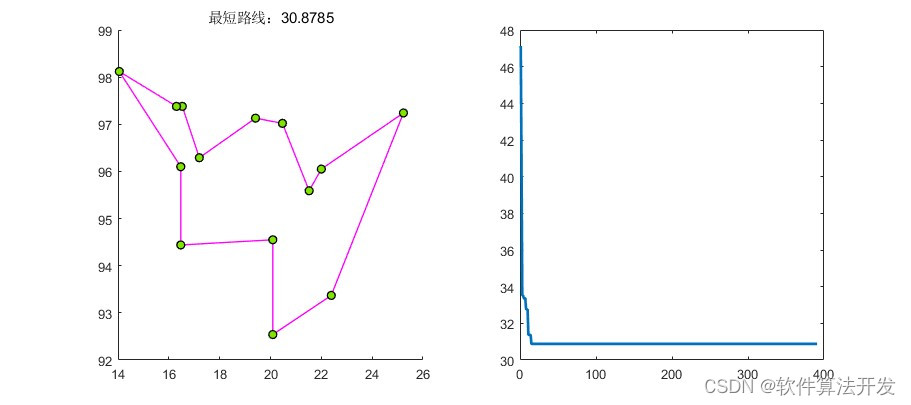
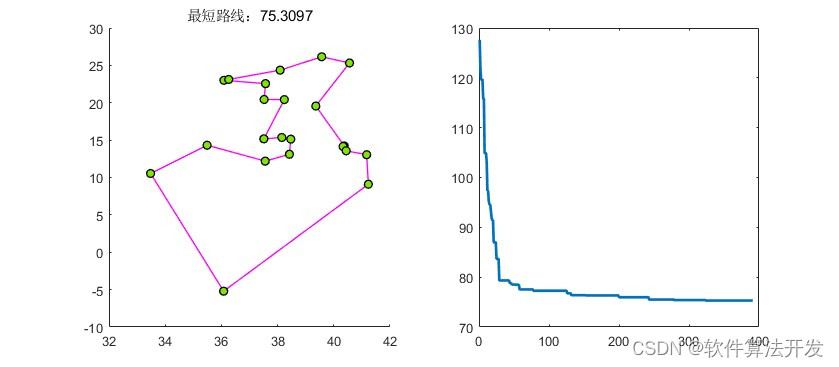
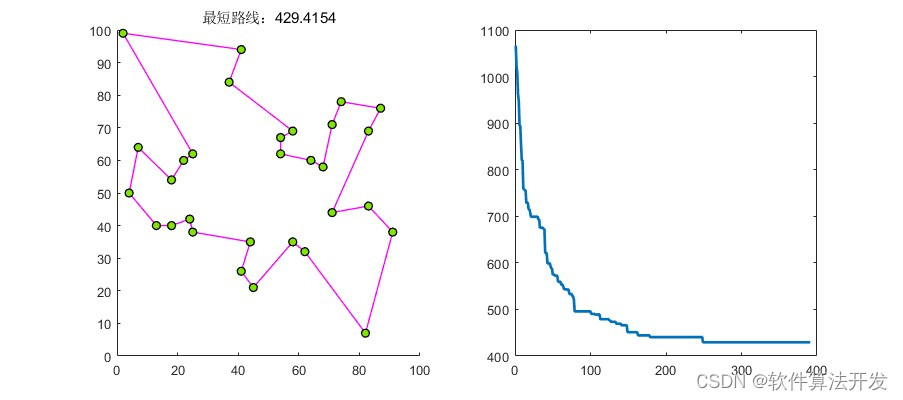
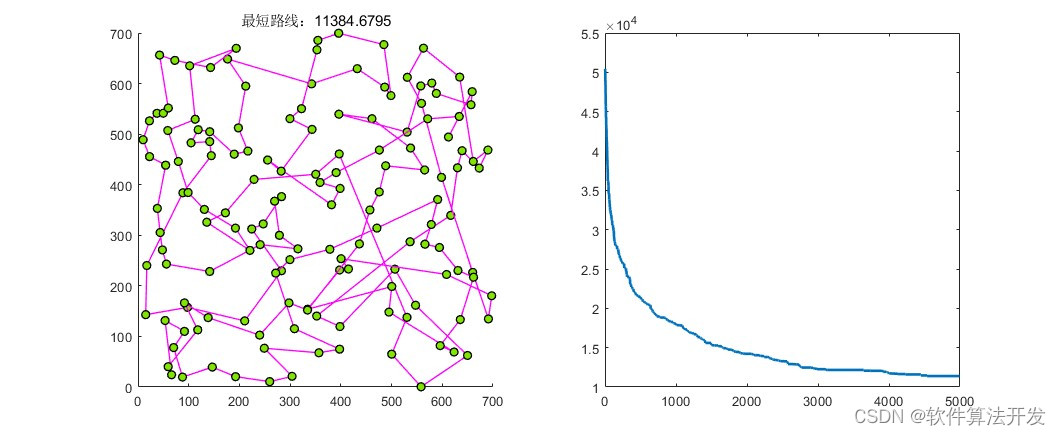
3.核心程序

for ij=1:Miters
    % 计算当前迭代周期种群适应度   
      %删除与交叉区域相同元素
      for j=1:Rcc
          for k=1:num
              if Xnew(i,k)==Yc(j)
                 Xnew(i,k)=0;
                  for t=1:num-k
                      temp=Xnew(i,k+t-1);
                      Xnew(i,k+t-1)=Xnew(i,k+t);
                      Xnew(i,k+t)=temp;
                  end                
              end
          end
      end
  
      %插入交叉区域
      for j=1:Rcc
          Xnew(i,num-Rcc+j)=Yc(j);
      end
      %判断产生新路径长度是否变短
      ydt=0;
      for j=1:num-1
          ydt=ydt+mdist(Xnew(i,j),Xnew(i,j+1));
      end
      ydt=ydt+mdist(Xnew(i,1),Xnew(i,num));
      if yfit(i)>ydt
         x(i,:)=Xnew(i,:);
      end
      %进行变异操作
      c1=round(rand*(num-1))+1;    
      c2=round(rand*(num-1))+1;
      temp=Xnew(i,c1);
      Xnew(i,c1)=Xnew(i,c2);
      Xnew(i,c2)=temp;
      %判断产生新路径长度是否变短
      ydt=0;
      for j=1:num-1
          ydt=ydt+mdist(Xnew(i,j),Xnew(i,j+1));
      end
      ydt=ydt+mdist(Xnew(i,1),Xnew(i,num));
  
      if yfit(i)>ydt
         x(i,:)=Xnew(i,:);
      end
    end
  
    yfit1=yfit(1);
    yfit2=1;
    for i=1:Pops
       if yfit1>=yfit(i)
            yfit1=yfit(i);
            yfit2=i;
        end
    end
    idx        = yfit2;
    L_best(ij) = min(yfit);
    %当前全局最优路径
    Ygbest     = x(idx,:);     
   
    if mod(ij,10)==1
        figure(1)
        subplot(121);
        scatter(pxy(:,1),pxy(:,2));
        hold on
        plot([pxy(Ygbest(1),1),pxy(Ygbest(num),1)],[pxy(Ygbest(1),2),pxy(Ygbest(num),2)],'-mo',...
            'LineWidth',1,...
            'MarkerSize',6,...
            'MarkerEdgeColor','k',...
            'MarkerFaceColor',[0.5,0.9,0.0]);
        for ii=2:num
            plot([pxy(Ygbest(ii-1),1),pxy(Ygbest(ii),1)],[pxy(Ygbest(ii-1),2),pxy(Ygbest(ii),2)],'-mo',...
            'LineWidth',1,...
            'MarkerSize',6,...
            'MarkerEdgeColor','k',...
            'MarkerFaceColor',[0.5,0.9,0.0]);
        end
        title(['最短路线：',num2str(min(yfit))]);
        hold off
        subplot(122);
        plot(L_best,'LineWidth',2);
    end
end
45

4.本算法原理
旅行商问题（Traveling Salesman Problem, TSP）是一个经典的组合优化问题，旨在寻找最短的可能路线，使得旅行商能访问每个城市恰好一次然后返回起点。利用遗传算法（Genetic Algorithm, GA）解决TSP问题，主要通过模拟自然界的进化过程，在解空间中搜索最优解。

一、编码方式首先需要将TSP问题转化为遗传算法可处理的形式。通常采用路径编码或顺序编码的方式，即将城市的访问顺序表示为一个染色体（个体），如对于n个城市，一个染色体可以用一个长度为n的整数数组表示 [c1, c2, ..., cn]，其中 ci 表示第i个访问的城市编号（假设从1开始计数，且cn+1=c1表示回到起点）。

二、初始种群生成随机生成一组代表不同路径的染色体构成初始种群，确保每个染色体都是一个合法的TSP解决方案，即包含所有城市且无重复。

三、适应度函数设计适应度函数评价各个染色体的好坏，对于TSP问题，适应度函数通常是路径总距离的倒数或对数形式.

四、选择操作根据适应度函数值对种群进行选择操作，保留适应度较高的个体进入下一代。常见的选择策略有轮盘赌选择、锦标赛选择等。

五、交叉（Crossover）选取两个父代个体进行交叉操作，产生新的子代。针对TSP问题常用的是顺序交叉（Order Crossover, OX）或部分匹配交叉（Partially Matched Crossover, PMX）。

六、变异（Mutation）在新生成的个体中执行变异操作，以增加种群多样性。对于TSP问题，一般采取逆序交换突变（Inversion Mutation）或swap突变.

七、 elitism（精英保留）为了防止优秀解在进化过程中丢失，可以设置一定数量的最优个体直接复制到下一代种群中。

八、迭代与终止条件上述步骤反复进行，直至满足预先设定的终止条件，如达到预定的进化代数、最优适应度不再显著提高或达到某一特定适应度阈值。