这是一篇关于Lingo的一些基本总结,以及如何做一些基本编程。
最近为了准备数学建模比赛自学了Lingo(matlab都还没很熟练的我是屑),看了看几个视频和一些教学ppt,于是写一篇随笔来总结一下。
本篇随笔会涉及到一些Lingo的基本概念,然后我会用一个题目来作为例子,由于我是因为数学建模才自学的,所以列举的题目例子一般是规划类的题目。
一、在讲Lingo之前,需要先要知道Lingo的一些基础概念:
(1)集合(set):
集合与属性(Attribute)是Lingo中极为重要的概念。其中又分为原始集和派生集。因为Lingo中并没有数组,所以想要处理大量有一定规律的数据,就得借助集合来实现。两者可以类比。我们可以用
SETS: 原始集名/1....n(或1,2,3,...)/:属性1,属性2; 派生集名(原始集名1,原始集名2...):属性1,属性2; ENDSETS
来定义一个原始集合。其中1....n相当于数组的下标,属性相当于数组名,属性里的元素用 属性名字(x1,x2,x3.....)来访问。
原始集一般可类比作为一维数组,而派生集可以当作多维数组来用。除此之外,还有稀疏集和稠密集的概念,这里不做赘述。
(2)函数:
Lingo里配备了一些函数,使用时需要在前面加一个@,其中包括一些数学函数,例如@SIN(),@SQRT()等,以及一些操作性的函数例如求和函数@SUM(),循环@FOR().....
这里在列举一些数学函数:
@abs(x) 返回 x 的绝对值 @sin(x) 返回 x 的正弦值,x 采用弧度制 @cos(x) 返回 x 的余弦值 @tan(x) 返回 x 的正切值 @exp(x) 返回常数 e 的 x 次方 @log(x) 返回 x 的自然对数 @lgm(x) 返回 x 的 gamma 函数的自然对数 @sign(x) 如果 x<0 返回-1;否则,返回 1 @floor(x) 返回 x 的整数部分。当 x>=0 时,返回不超过 x 的最大整数;当 x<0 时,返回不低于 x 的最大整数。 @smax(x1,x2,…,xn) 返回 x1,x2,…,xn 中的最大值 @smin(x1,x2,…,xn) 返回 x1,x2,…,xn 中的最小值
知道了一些基本概念之后,我们需要知道一个Lingo程序的基本架构,也就是程序的组成部分。
二、Lingo中建立的优化模型程序的五个”段“:
Lingo的程序大致由五个部分组成
(1)集合段
主要来定义必要的集合变量及其属性,以”SETS:“开始,以"ENDSETS"结尾。
(2)目标与约束段
这个地方主要写目标函数、约束条件,没有开始与结尾的标志。这里一般要用到LINGO的内部函数,尤其是与集合相关的求和函数 @SUM 和循环函数 @FOR 等。
(3)数据段:
大致的结构如图:
DATA:
attribute(属性) = value_list(常数列表);
......
ENDDATA
“DATA:” 开始, “ENDDATA”结束,对集合的属性(数组)输入必要的常数数据。格式为:“attribute(属性) = value_list(常数列表);”中数据之间可以用逗号“,”分开,也可以用空格分开(回车等价于一个空格)。
例如定义了一个集合TA/1...4/:a; 那么数据赋值就用a=45 6 8 2;来进行。需要注意的是,赋值数据的数量需要与集合中的下标数量相等。如果想在运行时才输入数据,可以在数据段写上”a=?“,这样在求解时系统会先等待用户输入a的值,再进行求解。
(4)初始段(不一定有)
大致格式为:
INIT:
attribute(属性) = value_list(常数列表);
ENDINIT
以“INIT: ”开始, “ENDINIT”结束,对集合的属性(数组)定义初值(因为求解算法一般是迭代算法,所以用户如果能给出一个比较好的迭代初值,对提高算法的计算效果是有益的)。如果有一个接近最优解的初值,对LINGO求解模型是有帮助的。定义初值的格式为:“attribute(属性) = value_list(常数列表);”这与数据段中的用法是类似的。
(5)计算段
大致格式为:
CALC:
x=@SUM(T(i):a(i)+b(i))/6; //例子
.....
ENDCALC
以“CALC: ”开始, “ENDCALC”结束,对一些原始数据进行计算处理。在实际问题中,输入的数据通常是原始数据,不一定能在模型中直接使用,可以在这个段对这些原始数据进行一定的“预处理”,得到模型中真正需要的数据,例如平均值等。
三、写一个基本程序的流程
针对一个问题写一个基本程序的流程大致为下:
1、确立模型。
想要针对一个问题编程,首先必须建立一个模型,建模方法在这按下不表。模型中必须要明确每一个式子的意思,以及变量、下标的严格区分。
2、确定集合。
明确好哪些变量需要什么样的下标。例如ai是需要从1~6变化,那么就需要建立一个可以从1遍历到6的集合,并把a设为它的属性。
3、确定变量。
确定好已知数据的变量(并赋值)和未知数据的变量、决策变量,以及其所属的集合。
4、正确写出模型里的每一个式子。
四、实际试验
下面我们来用一个实例来说明。
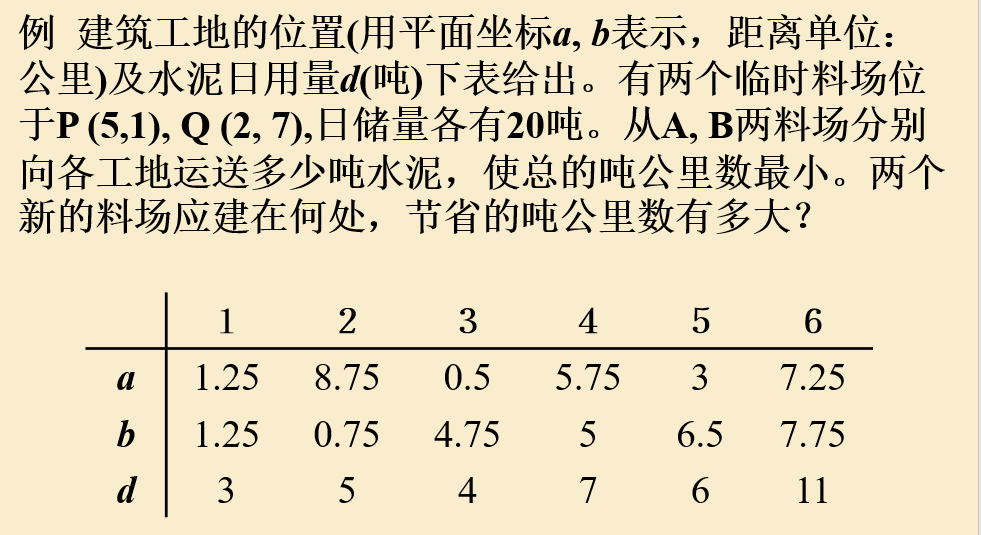
这是一道很经典的题目(反正ppt和视频里都有将这个),首先要做的第一步就是建模(不建模写个锤子程序),各个变量一定要明确。

程序如下所示:
MODEL: title location; !名字;
!下面这里定义变量; sets: demand/1..6/:a,b,d; supply/1..2/:x,y,e; link(demand,supply):c; endsets data: !(location of the demand)(需求点的位置)
这里给变量赋值; a=1.25,8.75,0.5,5.75,3,7.25; b=1.25,0.75,4.75,5,6.5,7.75; !(quantities of the demand and supply)(供需量); d=3 5 4 7 6 11;e=20,20; enddata init: !initial location for the supply(初始点); x=5 2;y=1 7; endinit !objectve funtion(这写目标函数); [OBJ] min=@sum(link(i,j):c(i,j)*((x(j)-a(i))^2+(y(j)-b(i))^2)^(1/2)); !demand constraints(这写需求约束条件,应等于每个工地的需求); @for(demand(i):@sum(supply(j):c(i,j))=d(i);); !supply constraints(供应约束条件,总的派送量应小于储存量); @for(supply(i):[SUPPLY_CON] @sum(demand(j):c(j,i)) <=e(i);); @for(supply:@free(x);@free(y);); END
其中,“title”是为这个模型起一个名字,包括后面[DEMAND_CON]和[SUPPLY_CON]。 "!.....;"的中间可以给程序添加注释说明;在“@for(demand(i):@sum(supply(j):c(i,j))=d(i);)”中,要注意体会@sum和@for的用法。"demind(i):"的意思可以认为在demand这个集合中,使用他的属性c(i,j)。并以i为下标使用集合中的数量,从1用到i。supply(j)也是如此,只不过supply对负责j。其实就跟c语言的数组是一个概念。
如果下标表示要从中间的某个数到后面的某个数怎么办?这里就要用到Lingo的逻辑语言。比如要用到大于2小于5的下标,程序可以写成demand(i)| i#gt#2#and#i#lt#5:,其中#gt#表示左边严格大于右边,#lt#表示左边严格小于右边。#and#表示与逻辑符。下面给出了Lingo的逻辑运算符的意义和优先级。
#not# 否定该操作数的逻辑值,#not#是一个 一元运算符
#eq# 若两个运算数相等,则为true;否则为flase
#ne# 若两个运算符不相等,则为true;否则为flase
#gt# 若左边的运算符严格大于右边的运算符,则为true;否则为flase
#ge# 若左边的运算符大于或等于右边的运算符,则为true;否则为flase
#lt# 若左边的运算符严格小于右边的运算符,则为true;否则为flase
#le# 若左边的运算符小于或等于右边的运算符,则为true;否则为flase
#and# 仅当两个参数都为true 时,结果为true;否则为flase
#or# 仅当两个参数都为false 时,结果为false;否则为true
这些运算符的优先级由高到低为:
高 #not#
#eq# #ne# #gt# #ge# #lt# #le#
低 #and# #or#
(不过其实>,<也适用。。)
有的人或许会奇怪,在题目的上半部分目标函数(min)的一块,c(i,j)明明是被包括在link这个集合里,但是下面约束条件中却使用了demand和supply,这是因为在目标函数里,c(i,j)一次需要同时有i,j两个变量,于是就需要被包括在link中来当作二维数组使用。而在第一个约束条件中,这里的意思是想表达两个料场对一个工地的输出加起来应该要满足该工地的需求。先要用for循环决定好是对那个工地(i),在用sum函数把两个料场(j)对一个工地(i)的输出加起来。在进行sum函数操作时,j实际上已经相当于一个常数,而不是一个变量。(可以类比于嵌套循环吧),所以这是只需要再使用supply遍历两个料场就行了。
“ : ”代表着遍历。
输出结果如下:
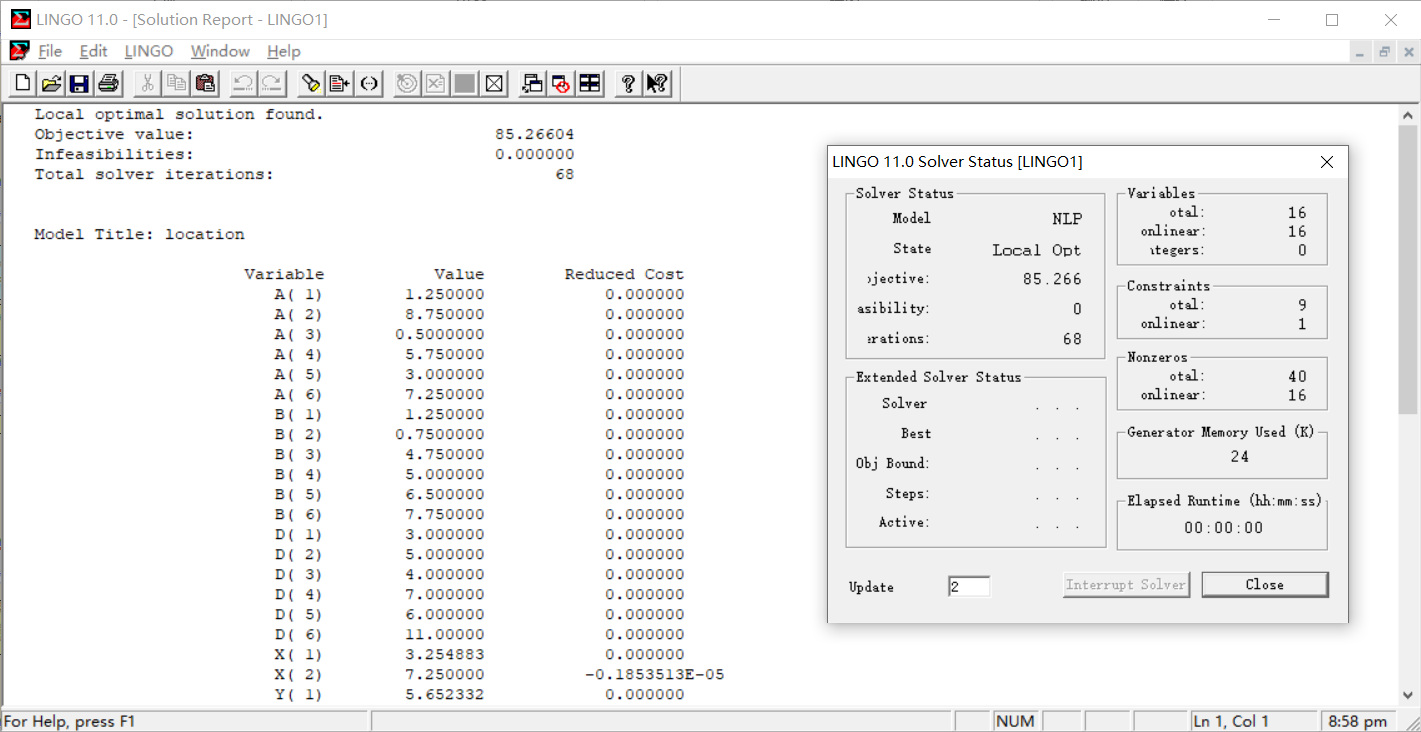
object value就是目标结果,为85.266,也就是最小吨公里。
下面还有数据为:
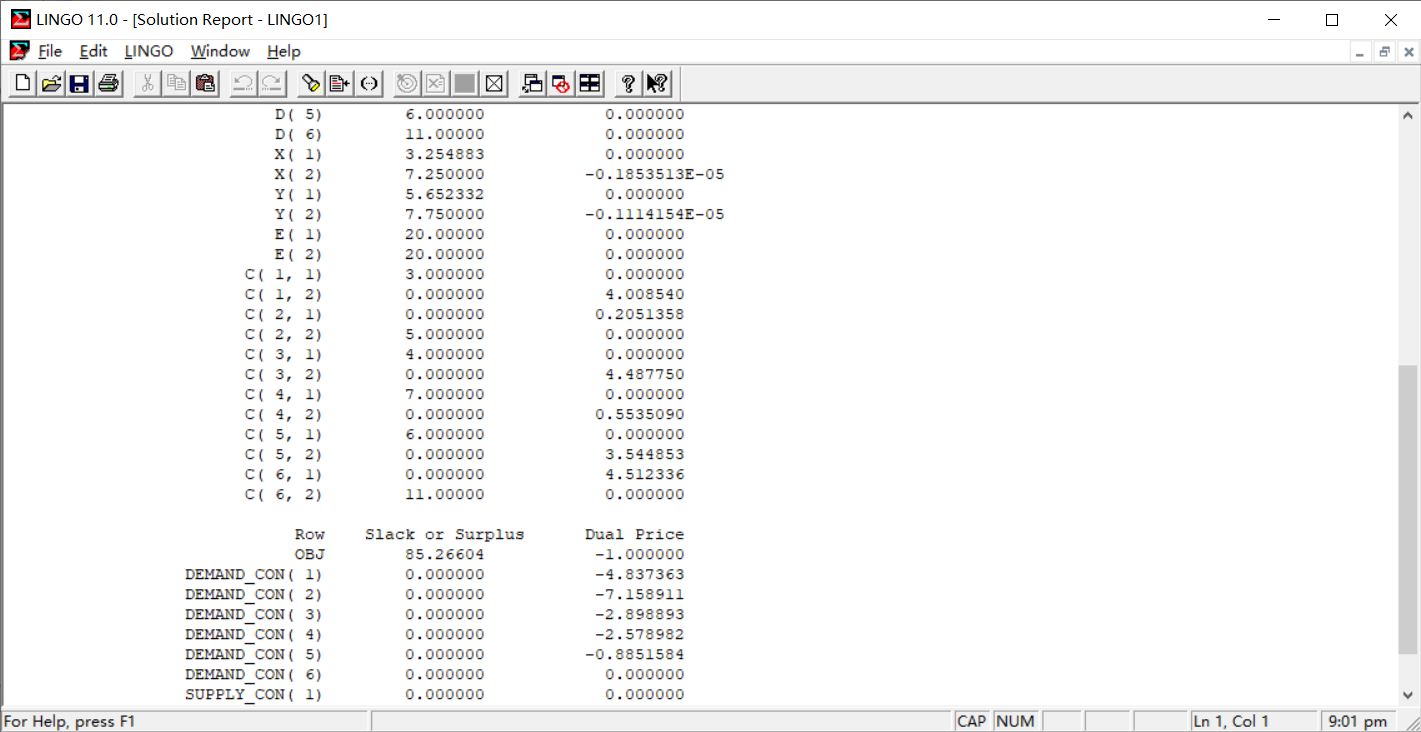
这些数据代表了程序在迭代时产生的每一步的做法,每一步的值。
以上就是这次的总结,里面包含了一些个人理解,或许会有不对。而实际上还有很多没讲,比如如何看和分析结果,如何确定输出结果到底是不是全局最优值。这些说起来又会很大一个篇幅(其实是你也不太懂吧),总之就是这样。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号