python numpy绘图示例

# 导入必要的库
import numpy as np  # 导入NumPy库，用于数值计算和矩阵操作
import matplotlib.pyplot as plt  # 导入Matplotlib的pyplot模块，用于绘图
from matplotlib import cm  # 导入颜色映射模块
import seaborn as sns  # 导入Seaborn库，用于统计数据可视化

# 设置随机种子以确保结果可重现
np.random.seed(42)


# 创建一个复杂的矩阵计算函数
def complex_matrix_function(x, y):
    """
    根据输入的x和y坐标生成三维曲面数据

    参数:
        x: x轴坐标数组
        y: y轴坐标数组

    返回:
        X, Y: 网格坐标矩阵
        Z: 计算得到的函数值矩阵
    """
    # 创建网格点坐标矩阵
    X, Y = np.meshgrid(x, y)

    # 计算一些复杂的矩阵运算
    Z1 = np.sin(np.sqrt(X**2 + Y**2))  # 计算第一个分量：距离原点的正弦函数
    Z2 = np.cos(X) * np.exp(
        -0.1 * (X**2 + Y**2)
    )  # 计算第二个分量：余弦与高斯衰减的乘积
    Z3 = (X**2 + Y**2) * np.exp(
        -0.2 * np.sqrt(X**2 + Y**2)
    )  # 计算第三个分量：平方和与指数衰减的乘积

    # 矩阵运算组合
    Z = Z1 + Z2 - 0.3 * Z3  # 将三个分量组合成最终的函数值

    return X, Y, Z


# 生成数据
x = np.linspace(-5, 5, 100)  # 创建x轴上的100个均匀分布点
y = np.linspace(-5, 5, 100)  # 创建y轴上的100个均匀分布点
X, Y, Z = complex_matrix_function(x, y)  # 调用函数计算曲面数据

# 创建一个包含多个子图的图形
plt.figure(figsize=(18, 12))  # 创建一个18x12英寸的图形

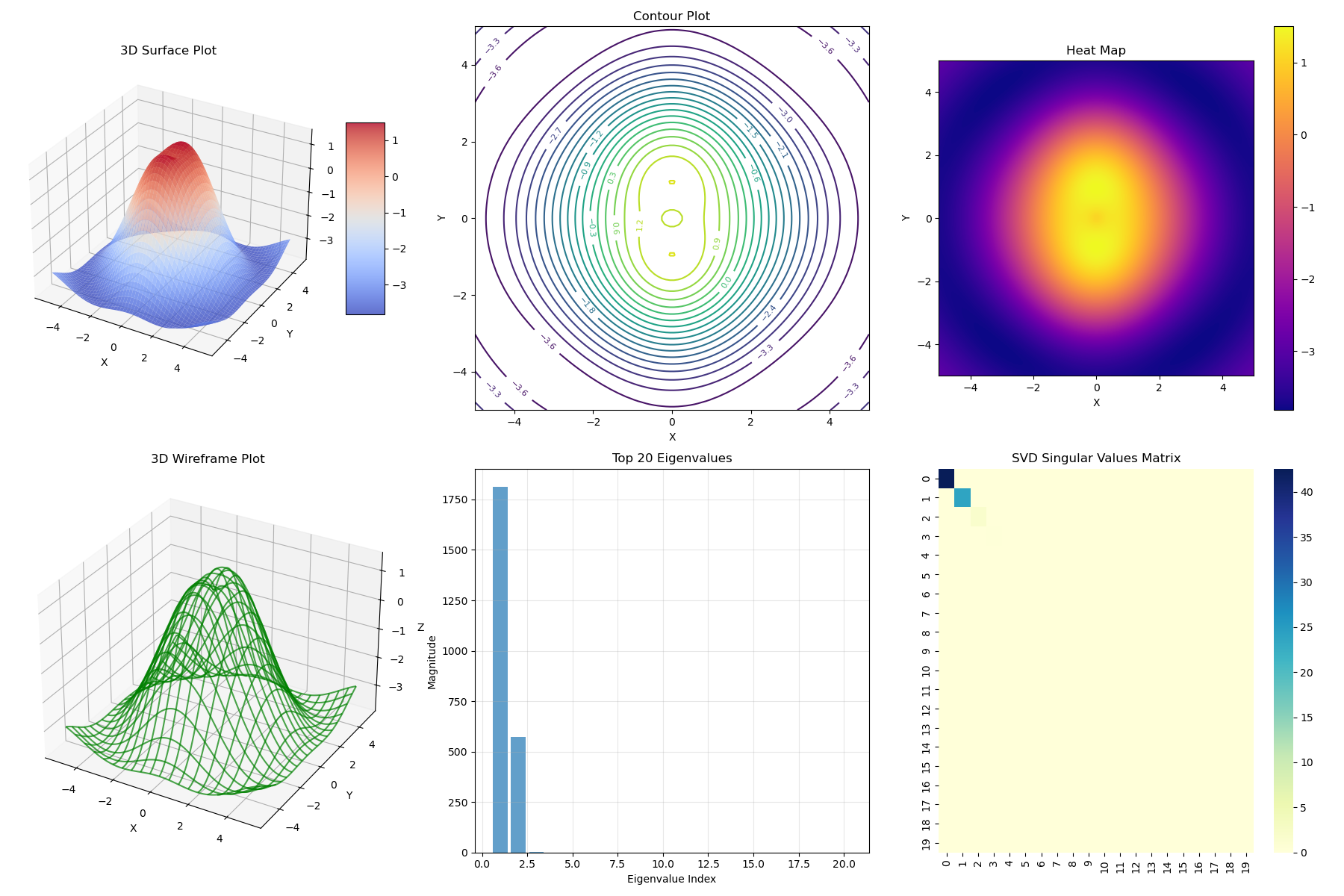
# 1. 3D曲面图
ax1 = plt.subplot(2, 3, 1, projection="3d")  # 创建2行3列的第1个子图，设置为3D投影
surf = ax1.plot_surface(
    X, Y, Z, cmap=cm.coolwarm, linewidth=0, antialiased=True, alpha=0.8
)  # 绘制3D曲面，使用coolwarm颜色映射
ax1.set_title("3D Surface Plot")  # 设置标题
ax1.set_xlabel("X")  # 设置X轴标签
ax1.set_ylabel("Y")  # 设置Y轴标签
ax1.set_zlabel("Z")  # 设置Z轴标签
plt.colorbar(surf, ax=ax1, shrink=0.5, aspect=5)  # 添加颜色条

# 2. 等高线图
ax2 = plt.subplot(2, 3, 2)  # 创建2行3列的第2个子图
contour = ax2.contour(
    X, Y, Z, 20, cmap="viridis"
)  # 绘制20条等高线，使用viridis颜色映射
ax2.clabel(contour, inline=True, fontsize=8)  # 为等高线添加标签
ax2.set_title("Contour Plot")  # 设置标题
ax2.set_xlabel("X")  # 设置X轴标签
ax2.set_ylabel("Y")  # 设置Y轴标签

# 3. 热图
ax3 = plt.subplot(2, 3, 3)  # 创建2行3列的第3个子图
im = ax3.imshow(
    Z, extent=[-5, 5, -5, 5], origin="lower", cmap="plasma", interpolation="bilinear"
)  # 绘制热图，使用plasma颜色映射和双线性插值
ax3.set_title("Heat Map")  # 设置标题
ax3.set_xlabel("X")  # 设置X轴标签
ax3.set_ylabel("Y")  # 设置Y轴标签
plt.colorbar(im, ax=ax3)  # 添加颜色条

# 4. 3D线框图
ax4 = plt.subplot(2, 3, 4, projection="3d")  # 创建2行3列的第4个子图，设置为3D投影
wire = ax4.plot_wireframe(
    X, Y, Z, rstride=5, cstride=5, color="green", alpha=0.7
)  # 绘制3D线框图，每5个点取样一次
ax4.set_title("3D Wireframe Plot")  # 设置标题
ax4.set_xlabel("X")  # 设置X轴标签
ax4.set_ylabel("Y")  # 设置Y轴标签
ax4.set_zlabel("Z")  # 设置Z轴标签

# 5. 矩阵特征值分析
ax5 = plt.subplot(2, 3, 5)  # 创建2行3列的第5个子图
# 从Z中提取一个子矩阵进行特征值分析
submatrix = Z[25:75, 25:75]  # 提取Z的中心50x50子矩阵
eigenvalues, eigenvectors = np.linalg.eig(
    submatrix @ submatrix.T
)  # 计算子矩阵与其转置乘积的特征值和特征向量
# 排序特征值
sorted_indices = np.argsort(eigenvalues)[::-1]  # 获取特征值降序排列的索引
sorted_eigenvalues = eigenvalues[sorted_indices]  # 对特征值进行降序排序
# 绘制前20个特征值
ax5.bar(range(1, 21), sorted_eigenvalues[:20], alpha=0.7)  # 绘制前20个特征值的条形图
ax5.set_title("Top 20 Eigenvalues")  # 设置标题
ax5.set_xlabel("Eigenvalue Index")  # 设置X轴标签
ax5.set_ylabel("Magnitude")  # 设置Y轴标签
ax5.grid(True, alpha=0.3)  # 添加网格线

# 6. 矩阵SVD分解可视化
ax6 = plt.subplot(2, 3, 6)  # 创建2行3列的第6个子图
U, S, Vt = np.linalg.svd(submatrix)  # 对子矩阵进行奇异值分解
# 使用热图显示奇异值矩阵
S_matrix = np.zeros((20, 20))  # 创建一个20x20的零矩阵
np.fill_diagonal(S_matrix, S[:20])  # 在对角线上填充前20个奇异值
sns.heatmap(S_matrix, cmap="YlGnBu", ax=ax6)  # 绘制奇异值矩阵的热图
ax6.set_title("SVD Singular Values Matrix")  # 设置标题

# 调整布局
plt.tight_layout()  # 自动调整子图参数，使之填充整个图像区域
plt.savefig(
    "complex_numpy_visualization.png", dpi=300
)  # 保存图像为PNG文件，分辨率为300dpi
plt.show()  # 显示图像

# 额外分析：计算矩阵的一些统计特性
print(f"矩阵Z的形状: {Z.shape}")  # 打印矩阵Z的维度
print(f"矩阵Z的最大值: {np.max(Z):.4f}")  # 打印矩阵Z的最大值，保留4位小数
print(f"矩阵Z的最小值: {np.min(Z):.4f}")  # 打印矩阵Z的最小值，保留4位小数
print(f"矩阵Z的平均值: {np.mean(Z):.4f}")  # 打印矩阵Z的平均值，保留4位小数
print(f"矩阵Z的标准差: {np.std(Z):.4f}")  # 打印矩阵Z的标准差，保留4位小数
print(
    f"矩阵Z的行列式: {np.linalg.det(submatrix[:10, :10]):.4e}"
)  # 打印子矩阵前10x10部分的行列式，使用科学计数法
print(f"矩阵Z的秩: {np.linalg.matrix_rank(submatrix)}")  # 打印子矩阵的秩
print(
    f"矩阵Z的条件数: {np.linalg.cond(submatrix):.4e}"
)  # 打印子矩阵的条件数，使用科学计数法