【笔记0106】机器学习期末复习

1 线性分类

题目：


首先，我们有感知机的线性判别函数 \(f(x) = \mathbf{w}^T \mathbf{x} + b\)，其中初始参数为 \(\mathbf{w} = [0, 0]\)，\(b = 0\)。目标函数是 \(J(\mathbf{w}) = \sum_{\mathbf{x}_i \in E} -\mathbf{w}^T \mathbf{x}_i y_i\)，其中 \(E\) 是错误分类样本集，学习率为 \(\eta = 1\)。更新规则为：

\[\mathbf{w} \leftarrow \mathbf{w} - \eta \nabla J(\mathbf{w}), \quad b \leftarrow b - \eta \nabla J(b) \]

错误分类样本集 \(E\) 是指满足 \(y_i (\mathbf{w}^T \mathbf{x}_i + b) \leq 0\) 的样本集合。

给定训练样本：

1. \(\mathbf{x}_1 = [1, 2]\), \(y_1 = 1\)
2. \(\mathbf{x}_2 = [2, 3]\), \(y_2 = -1\)
3. \(\mathbf{x}_3 = [-1, -1]\), \(y_3 = 1\)

按照随机梯度下降的方式进行模型学习，迭代更新参数。进行6步迭代，更新过程如下：

迭代过程

初始参数：

\[\mathbf{w} = [0, 0], \quad b = 0 \]

第一步：选择样本 \(\mathbf{x}_1 = [1, 2]\), \(y_1 = 1\)

• 判断是否错误分类：

  \[y_1 (\mathbf{w}^T \mathbf{x}_1 + b) = 1 (0 \times 1 + 0 \times 2 + 0) = 0 \leq 0 \]

  错误分类。

• 更新 \(\mathbf{w}\) 和 \(b\)：

  \[\mathbf{w} = \mathbf{w} + y_1 \mathbf{x}_1 = [0 + 1 \times 1, 0 + 1 \times 2] = [1, 2] \]
  \[b = b + y_1 = 0 + 1 = 1 \]

第二步：选择样本 \(\mathbf{x}_2 = [2, 3]\), \(y_2 = -1\)

• 判断是否错误分类：

  \[y_2 (\mathbf{w}^T \mathbf{x}_2 + b) = -1 (1 \times 2 + 2 \times 3 + 1) = -1 (2 + 6 + 1) = -9 \leq 0 \]

  错误分类。

• 更新 \(\mathbf{w}\) 和 \(b\)：

  \[\mathbf{w} = \mathbf{w} + y_2 \mathbf{x}_2 = [1 + (-1) \times 2, 2 + (-1) \times 3] = [-1, -1] \]
  \[b = b + y_2 = 1 + (-1) = 0 \]

第三步：选择样本 \(\mathbf{x}_3 = [-1, -1]\), \(y_3 = 1\)

• 判断是否错误分类：
  \[y_3 (\mathbf{w}^T \mathbf{x}_3 + b) = 1 ((-1) \times (-1) + (-1) \times (-1) + 0) = 1 (1 + 1 + 0) = 2 > 0 \]
  正确分类，不更新。

第四步：选择样本 \(\mathbf{x}_1 = [1, 2]\), \(y_1 = 1\)

• 判断是否错误分类：

  \[y_1 (\mathbf{w}^T \mathbf{x}_1 + b) = 1 ((-1) \times 1 + (-1) \times 2 + 0) = 1 (-1 - 2 + 0) = -3 \leq 0 \]

  错误分类。

• 更新 \(\mathbf{w}\) 和 \(b\)：

  \[\mathbf{w} = \mathbf{w} + y_1 \mathbf{x}_1 = [-1 + 1 \times 1, -1 + 1 \times 2] = [0, 1] \]
  \[b = b + y_1 = 0 + 1 = 1 \]

第五步：选择样本 \(\mathbf{x}_2 = [2, 3]\), \(y_2 = -1\)

• 判断是否错误分类：

  \[y_2 (\mathbf{w}^T \mathbf{x}_2 + b) = -1 (0 \times 2 + 1 \times 3 + 1) = -1 (0 + 3 + 1) = -4 \leq 0 \]

  错误分类。

• 更新 \(\mathbf{w}\) 和 \(b\)：

  \[\mathbf{w} = \mathbf{w} + y_2 \mathbf{x}_2 = [0 + (-1) \times 2, 1 + (-1) \times 3] = [-2, -2] \]
  \[b = b + y_2 = 1 + (-1) = 0 \]

第六步：选择样本 \(\mathbf{x}_3 = [-1, -1]\), \(y_3 = 1\)

• 判断是否错误分类：
  \[y_3 (\mathbf{w}^T \mathbf{x}_3 + b) = 1 ((-2) \times (-1) + (-2) \times (-1) + 0) = 1 (2 + 2 + 0) = 4 > 0 \]
  正确分类，不更新。

最终结果

经过6步迭代后，参数为：

\[\mathbf{w} = [-2, -2], \quad b = 0 \]

线性判别函数为：

\[f(\mathbf{x}) = -2x_1 - 2x_2 \]

2 非线性分类

3 概率图联合分布的因子分解式

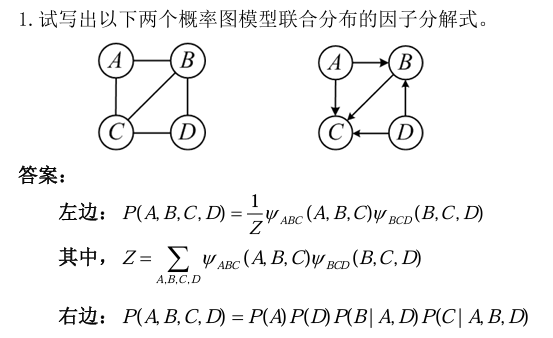
这个图中左边的是无向图，右边的是有向图。
概率图模型通过图结构表示随机变量间的条件依赖关系，联合分布的因子分解式依赖于图的类型。

1. 有向图模型（贝叶斯网络）

有向图模型使用有向无环图（DAG）表示变量间的因果关系。联合分布可分解为各变量在其父节点条件下的条件概率的乘积：

\[P(X_1, X_2, \dots, X_n) = \prod_{i=1}^n P(X_i \mid \text{Pa}(X_i)) \]

其中，\(\text{Pa}(X_i)\) 是 \(X_i\) 的父节点集合。

2. 无向图模型（马尔可夫随机场）

无向图模型使用无向图表示变量间的依赖关系。联合分布分解为图中最大团的势函数乘积，再归一化：

\[P(X_1, X_2, \dots, X_n) = \frac{1}{Z} \prod_{c \in \mathcal{C}} \psi_c(X_c) \]

其中，\(\mathcal{C}\) 是最大团集合，\(\psi_c(X_c)\) 是团 \(c\) 的势函数，\(Z\) 是归一化常数。

3. 有向图与无向图的区别

• 有向图：表示因果关系，适合表达变量间的因果依赖。
• 无向图：表示关联关系，适合表达变量间的对称依赖。
  选择哪种模型取决于具体问题和变量间的关系。

无向图表示的是什么？

无向图用来表示变量之间的“关联关系”。比如右图：A-B, B-C, C-D, A-C, B-D，它表示变量 A、B、C、D 之间的依赖关系。图中的每条边（比如 A-B）表示两个变量之间有直接的关联。

• A-B：A 和 B 有关系。
• B-C：B 和 C 有关系。
• C-D：C 和 D 有关系。
• A-C：A 和 C 有关系。
• B-D：B 和 D 有关系。

这个图的意思是：

• A 和 B 有关系，A 和 C 有关系，B 和 C 有关系，等等。
• 但 A 和 D 没有直接的关系（因为没有 A-D 这条边）。

最大团是啥？

“团”是指图中一些节点，它们之间两两都有边相连。而“最大团”是指一个团，它不能通过加入更多的节点而变得更大。

在你的图中：

• 最大团 1：A、B、C（因为 A-B, B-C, A-C 都有边相连）。
• 最大团 2：B、C、D（因为 B-C, C-D, B-D 都有边相连）。

最大团的意义是：这些变量之间的关系非常紧密，可以作为一个整体来考虑。

---

势函数是啥？

势函数是用来描述一个团中变量之间的“亲密程度”的函数。它表示这些变量在一起的可能性有多大。

比如：

• 对于最大团 A、B、C，势函数 \(\psi(A, B, C)\) 表示 A、B、C 同时取某些值的可能性。
• 对于最大团 B、C、D，势函数 \(\psi(B, C, D)\) 表示 B、C、D 同时取某些值的可能性。

势函数的值越大，说明这些变量取某些值的可能性越高。

---

归一化常数是啥？

归一化常数（通常记作 \(Z\)）的作用是让所有可能的概率加起来等于 1。因为势函数的乘积可能不是一个概率分布（总和不一定为 1），所以需要用 \(Z\) 来调整。

公式是：
\( P(A, B, C, D) = \frac{1}{Z} \cdot \psi(A, B, C) \cdot \psi(B, C, D) \)

这里的 \(Z\) 就是归一化常数，它的值是所有可能的 \(\psi(A, B, C) \cdot \psi(B, C, D)\) 的总和。

---

结合例子解释

假设右面的图表示一个社交网络：

• A、B、C、D 是四个人。
• 边表示两个人是朋友。

最大团：

• A、B、C 是一个朋友圈。
• B、C、D 是另一个朋友圈。

势函数：

• \(\psi(A, B, C)\) 表示 A、B、C 三个人一起出现的可能性（比如他们经常一起吃饭）。
• \(\psi(B, C, D)\) 表示 B、C、D 三个人一起出现的可能性。

归一化常数：

• 假设 \(\psi(A, B, C)\) 和 \(\psi(B, C, D)\) 的值算出来很大，但为了让所有可能的概率加起来等于 1，需要用 \(Z\) 来调整。

总结

• 无向图：表示变量之间的关联关系。
• 最大团：图中关系最紧密的变量组。
• 势函数：描述一个团中变量之间的“亲密程度”。
• 归一化常数：让所有概率加起来等于 1。
  通过这种方式，无向图模型可以很好地描述变量之间的复杂关系！

4 隐马尔科夫模型

1. 隐马尔可夫模型（HMM）简介

隐马尔可夫模型是一种统计模型，用于描述一个含有隐含未知参数的马尔可夫过程。它由两个随机过程组成：

• 状态序列：这是隐藏的，不可直接观测的。
• 观测序列：这是可以直接观测到的，由状态序列生成。

2. 信封抽球问题

假设你有两个信封，每个信封里有不同颜色的球。你随机选择一个信封，然后从中抽取一个球，记录颜色，再把球放回信封。这个过程重复多次，形成一个球的颜色序列。

3. 模型参数解释

• 𝝅（初始状态概率）：表示初始时刻选择每个信封的概率。这里𝝅=(0.5,0.5)表示初始时刻选择两个信封的概率都是50%。

• 𝐀（状态转移矩阵）：表示从一个状态转移到另一个状态的概率。这里A=[0,1; 0.5,0.5]表示：

  • 从信封1转移到信封2的概率是1（即一定会转移到信封2）。
  • 从信封2转移到信封1的概率是0.5，转移到信封2的概率也是0.5。

• 𝐁（观测概率矩阵）：表示在某个状态下生成某个观测值的概率。这里B=[0.5,0.5; 0,1]表示：

  • 在信封1中，抽到红球和黑球的概率都是50%。
  • 在信封2中，抽到红球的概率是0，抽到黑球的概率是100%。

4. 问题解析

题目给出了一个球的颜色序列𝐱={红,黑,黑,黑,红}，要求利用前向算法和后向算法计算𝑃(𝐱|𝜆)，即在给定模型𝜆下，生成这个观测序列的概率。

5. 前向算法和后向算法

• 前向算法：计算从初始时刻到当前时刻，生成部分观测序列并处于某个状态的概率。
• 后向算法：计算从当前时刻到最终时刻，生成剩余观测序列并处于某个状态的概率。

通过结合前向和后向算法，可以计算出整个观测序列的概率。

计算过程

接下来我们来逐步计算 $ P(\mathbf{x} \mid \lambda) $，其中观测序列为 \(\mathbf{x} = \{红, 黑, 黑, 黑, 红\}\)，模型参数为：

• 初始状态概率 \(\boldsymbol{\pi} = (0.5, 0.5)\)
• 状态转移矩阵 \(\mathbf{A} = \begin{bmatrix} 0 & 1 \\ 0.5 & 0.5 \end{bmatrix}\)
• 观测概率矩阵 \(\mathbf{B} = \begin{bmatrix} 0.5 & 0.5 \\ 0 & 1 \end{bmatrix}\)

假设状态 \(1\) 是信封1，状态 \(2\) 是信封2；观测值 \(红\) 对应索引 \(1\)，\(黑\) 对应索引 \(2\)。

1. 前向算法

前向算法计算的是在时刻 \(t\) 处于状态 \(i\) 并生成观测序列 \(x_1, x_2, \dots, x_t\) 的概率，记为 \(\alpha_t(i)\)。

初始化（\(t=1\)）

对于每个状态 \(i\)，计算：
\( \alpha_1(i) = \pi_i \cdot b_i(x_1) \)
其中 \(x_1 = 红\)（索引 \(1\)）。

• 对于状态 \(1\)：
  \( \alpha_1(1) = \pi_1 \cdot b_1(红) = 0.5 \cdot 0.5 = 0.25 \)
• 对于状态 \(2\)：
  \( \alpha_1(2) = \pi_2 \cdot b_2(红) = 0.5 \cdot 0 = 0 \)

所以：
\( \alpha_1 = [0.25, 0] \)

---

递推（\(t=2\) 到 \(t=5\)）

对于每个时刻 \(t\) 和状态 \(j\)，计算：
\( \alpha_t(j) = \sum_{i=1}^2 \alpha_{t-1}(i) \cdot a_{ij} \cdot b_j(x_t) \)

我们逐步计算：

\(t=2\)，观测 \(x_2 = 黑\)（索引 \(2\)）

• 对于状态 \(1\)：
  \( \alpha_2(1) = \alpha_1(1) \cdot a_{11} \cdot b_1(黑) + \alpha_1(2) \cdot a_{21} \cdot b_1(黑) \)
  \( \alpha_2(1) = 0.25 \cdot 0 \cdot 0.5 + 0 \cdot 0.5 \cdot 0.5 = 0 \)
• 对于状态 \(2\)：
  \( \alpha_2(2) = \alpha_1(1) \cdot a_{12} \cdot b_2(黑) + \alpha_1(2) \cdot a_{22} \cdot b_2(黑) \)
  \( \alpha_2(2) = 0.25 \cdot 1 \cdot 1 + 0 \cdot 0.5 \cdot 1 = 0.25 \)

所以：
\( \alpha_2 = [0, 0.25] \)

---

\(t=3\)，观测 \(x_3 = 黑\)（索引 \(2\)）

• 对于状态 \(1\)：
  \( \alpha_3(1) = \alpha_2(1) \cdot a_{11} \cdot b_1(黑) + \alpha_2(2) \cdot a_{21} \cdot b_1(黑) \)
  \( \alpha_3(1) = 0 \cdot 0 \cdot 0.5 + 0.25 \cdot 0.5 \cdot 0.5 = 0.0625 \)
• 对于状态 \(2\)：
  \( \alpha_3(2) = \alpha_2(1) \cdot a_{12} \cdot b_2(黑) + \alpha_2(2) \cdot a_{22} \cdot b_2(黑) \)
  \( \alpha_3(2) = 0 \cdot 1 \cdot 1 + 0.25 \cdot 0.5 \cdot 1 = 0.125 \)

所以：
\( \alpha_3 = [0.0625, 0.125] \)

---

\(t=4\)，观测 \(x_4 = 黑\)（索引 \(2\)）

• 对于状态 \(1\)：
  \( \alpha_4(1) = \alpha_3(1) \cdot a_{11} \cdot b_1(黑) + \alpha_3(2) \cdot a_{21} \cdot b_1(黑) \)
  \( \alpha_4(1) = 0.0625 \cdot 0 \cdot 0.5 + 0.125 \cdot 0.5 \cdot 0.5 = 0.03125 \)
• 对于状态 \(2\)：
  \( \alpha_4(2) = \alpha_3(1) \cdot a_{12} \cdot b_2(黑) + \alpha_3(2) \cdot a_{22} \cdot b_2(黑) \)
  \( \alpha_4(2) = 0.0625 \cdot 1 \cdot 1 + 0.125 \cdot 0.5 \cdot 1 = 0.125 \)

所以：
\( \alpha_4 = [0.03125, 0.125] \)

---

\(t=5\)，观测 \(x_5 = 红\)（索引 \(1\)）

• 对于状态 \(1\)：
  \( \alpha_5(1) = \alpha_4(1) \cdot a_{11} \cdot b_1(红) + \alpha_4(2) \cdot a_{21} \cdot b_1(红) \)
  \( \alpha_5(1) = 0.03125 \cdot 0 \cdot 0.5 + 0.125 \cdot 0.5 \cdot 0.5 = 0.03125 \)
• 对于状态 \(2\)：
  \( \alpha_5(2) = \alpha_4(1) \cdot a_{12} \cdot b_2(红) + \alpha_4(2) \cdot a_{22} \cdot b_2(红) \)
  \( \alpha_5(2) = 0.03125 \cdot 1 \cdot 0 + 0.125 \cdot 0.5 \cdot 0 = 0 \)

所以：
\( \alpha_5 = [0.03125, 0] \)

---

最终概率

观测序列的概率为：
\( P(\mathbf{x} \mid \lambda) = \sum_{i=1}^2 \alpha_5(i) = 0.03125 + 0 = 0.03125 \)

---

2. 后向算法

后向算法计算的是在时刻 \(t\) 处于状态 \(i\) 并生成观测序列 \(x_{t+1}, x_{t+2}, \dots, x_T\) 的概率，记为 \(\beta_t(i)\)。

初始化（\(t=5\)）

对于每个状态 \(i\)，初始化：
\( \beta_5(i) = 1 \)
所以：
\( \beta_5 = [1, 1] \)

---

递推（\(t=4\) 到 \(t=1\)）

对于每个时刻 \(t\) 和状态 \(i\)，计算：
\( \beta_t(i) = \sum_{j=1}^2 a_{ij} \cdot b_j(x_{t+1}) \cdot \beta_{t+1}(j) \)

我们逐步计算：

\(t=4\)，观测 \(x_5 = 红\)（索引 \(1\)）

• 对于状态 \(1\)：
  \( \beta_4(1) = a_{11} \cdot b_1(红) \cdot \beta_5(1) + a_{12} \cdot b_2(红) \cdot \beta_5(2) \)
  \( \beta_4(1) = 0 \cdot 0.5 \cdot 1 + 1 \cdot 0 \cdot 1 = 0 \)
• 对于状态 \(2\)：
  \( \beta_4(2) = a_{21} \cdot b_1(红) \cdot \beta_5(1) + a_{22} \cdot b_2(红) \cdot \beta_5(2) \)
  \( \beta_4(2) = 0.5 \cdot 0.5 \cdot 1 + 0.5 \cdot 0 \cdot 1 = 0.25 \)

所以：
\( \beta_4 = [0, 0.25] \)

---

\(t=3\)，观测 \(x_4 = 黑\)（索引 \(2\)）

• 对于状态 \(1\)：
  \( \beta_3(1) = a_{11} \cdot b_1(黑) \cdot \beta_4(1) + a_{12} \cdot b_2(黑) \cdot \beta_4(2) \)
  \( \beta_3(1) = 0 \cdot 0.5 \cdot 0 + 1 \cdot 1 \cdot 0.25 = 0.25 \)
• 对于状态 \(2\)：
  \( \beta_3(2) = a_{21} \cdot b_1(黑) \cdot \beta_4(1) + a_{22} \cdot b_2(黑) \cdot \beta_4(2) \)
  \( \beta_3(2) = 0.5 \cdot 0.5 \cdot 0 + 0.5 \cdot 1 \cdot 0.25 = 0.125 \)

所以：
\( \beta_3 = [0.25, 0.125] \)

---

\(t=2\)，观测 \(x_3 = 黑\)（索引 \(2\)）

• 对于状态 \(1\)：
  \( \beta_2(1) = a_{11} \cdot b_1(黑) \cdot \beta_3(1) + a_{12} \cdot b_2(黑) \cdot \beta_3(2) \)
  \( \beta_2(1) = 0 \cdot 0.5 \cdot 0.25 + 1 \cdot 1 \cdot 0.125 = 0.125 \)
• 对于状态 \(2\)：
  \( \beta_2(2) = a_{21} \cdot b_1(黑) \cdot \beta_3(1) + a_{22} \cdot b_2(黑) \cdot \beta_3(2) \)
  \( \beta_2(2) = 0.5 \cdot 0.5 \cdot 0.25 + 0.5 \cdot 1 \cdot 0.125 = 0.125 \)

所以：
\( \beta_2 = [0.125, 0.125] \)

---

\(t=1\)，观测 \(x_2 = 黑\)（索引 \(2\)）

• 对于状态 \(1\)：
  \( \beta_1(1) = a_{11} \cdot b_1(黑) \cdot \beta_2(1) + a_{12} \cdot b_2(黑) \cdot \beta_2(2) \)
  \( \beta_1(1) = 0 \cdot 0.5 \cdot 0.125 + 1 \cdot 1 \cdot 0.125 = 0.125 \)
• 对于状态 \(2\)：
  \( \beta_1(2) = a_{21} \cdot b_1(黑) \cdot \beta_2(1) + a_{22} \cdot b_2(黑) \cdot \beta_2(2) \)
  \( \beta_1(2) = 0.5 \cdot 0.5 \cdot 0.125 + 0.5 \cdot 1 \cdot 0.125 = 0.09375 \)

所以：
\( \beta_1 = [0.125, 0.09375] \)

最终概率

观测序列的概率为：
\( P(\mathbf{x} \mid \lambda) = \sum_{i=1}^2 \pi_i \cdot b_i(x_1) \cdot \beta_1(i) \)
\( P(\mathbf{x} \mid \lambda) = 0.5 \cdot 0.5 \cdot 0.125 + 0.5 \cdot 0 \cdot 0.09375 = 0.03125 \)

3. 结果

无论是前向算法还是后向算法，最终计算得到的观测序列概率均为：
\( P(\mathbf{x} \mid \lambda) = 0.03125 \)

这个结果表明，在给定的隐马尔可夫模型下，生成观测序列 \(\{红, 黑, 黑, 黑, 红\}\) 的概率是 \(0.03125\)。

维特比算法

在上述隐马尔可夫模型中，试用维特比算法确定最有可能的信封序列。

维特比算法是一种动态规划算法，用于在隐马尔可夫模型中找到最可能的状态序列（即最有可能的信封序列）。

维特比算法的核心是动态规划，分为以下几步：

1.初始化：计算初始时刻每个状态的最大概率和路径。

2.递推：对于每个时刻t，计算每个状态的最大概率，并记录路径。

3.终止：找到最终时刻的最大概率和对应的状态。

4.回溯：根据记录的路径，回溯得到最可能的状态序列。

5 ID3、C4.5、CART

6 Maximum Likelihood方法

抛一枚硬币问题，观察数据情况是：一枚硬币包括正反两面，共抛了30 次，其中12 次是正面，18 次是反面。采用Maximum Likelihood 方法，估计正面出现的概率和反面出现的概率。

Maximum Likelihood（最大似然）方法是一种用于估计统计模型参数的常用方法。其核心思想是寻找一组参数，使得在该参数下，观测数据出现的概率（即似然）最大化。

具体步骤：

1. 定义模型：假设数据服从某个概率分布（如正态分布、泊松分布等），其形式由参数决定。
2. 构建似然函数：基于观测数据和模型，构建似然函数 $ L(\theta) $，表示在参数 $ \theta $ 下观测数据出现的概率。
3. 最大化似然函数：通过优化方法（如求导、数值优化等）找到使 $ L(\theta) $ 最大的参数 $ \hat{\theta} $，即为最大似然估计。

举例：

假设观测数据 $ X = {x_1, x_2, \dots, x_n} $ 服从正态分布 $ N(\mu, \sigma^2) $，目标是估计均值 $ \mu $ 和方差 $ \sigma^2 $。

1. 似然函数：
   \( L(\mu, \sigma^2) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x_i - \mu)^2}{2\sigma^2}\right) \)
2. 对数似然函数（便于计算）：
   \( \ln L(\mu, \sigma^2) = -\frac{n}{2} \ln(2\pi) - \frac{n}{2} \ln(\sigma^2) - \frac{1}{2\sigma^2} \sum_{i=1}^n (x_i - \mu)^2 \)
3. 求导并最大化：
   对 $ \mu $ 和 $ \sigma^2 $ 求导，令导数为零，解得：
   \( \hat{\mu} = \frac{1}{n} \sum_{i=1}^n x_i, \quad \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \hat{\mu})^2 \)

优点：

• 一致性：随着数据量增加，估计值趋近于真实值。
• 渐近正态性：在大样本下，估计值服从正态分布。
• 广泛适用：可用于多种模型和分布。

缺点：

• 计算复杂：对复杂模型，优化可能困难。
• 对初值敏感：可能陷入局部最优。

总结：

Maximum Likelihood方法通过最大化观测数据的似然函数来估计模型参数，是统计学和机器学习中的重要工具。

7 Fisher最优鉴别矢量

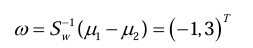
8 贝叶斯网络