学习笔记：主席树

第一次接触可持久化数据结构 awa，可以访问修改历史版本，功能比较强大。（尤其在访问历史版本和解决区间排名等问题的方面）

可持久化线段树

传送门：可持久化线段树
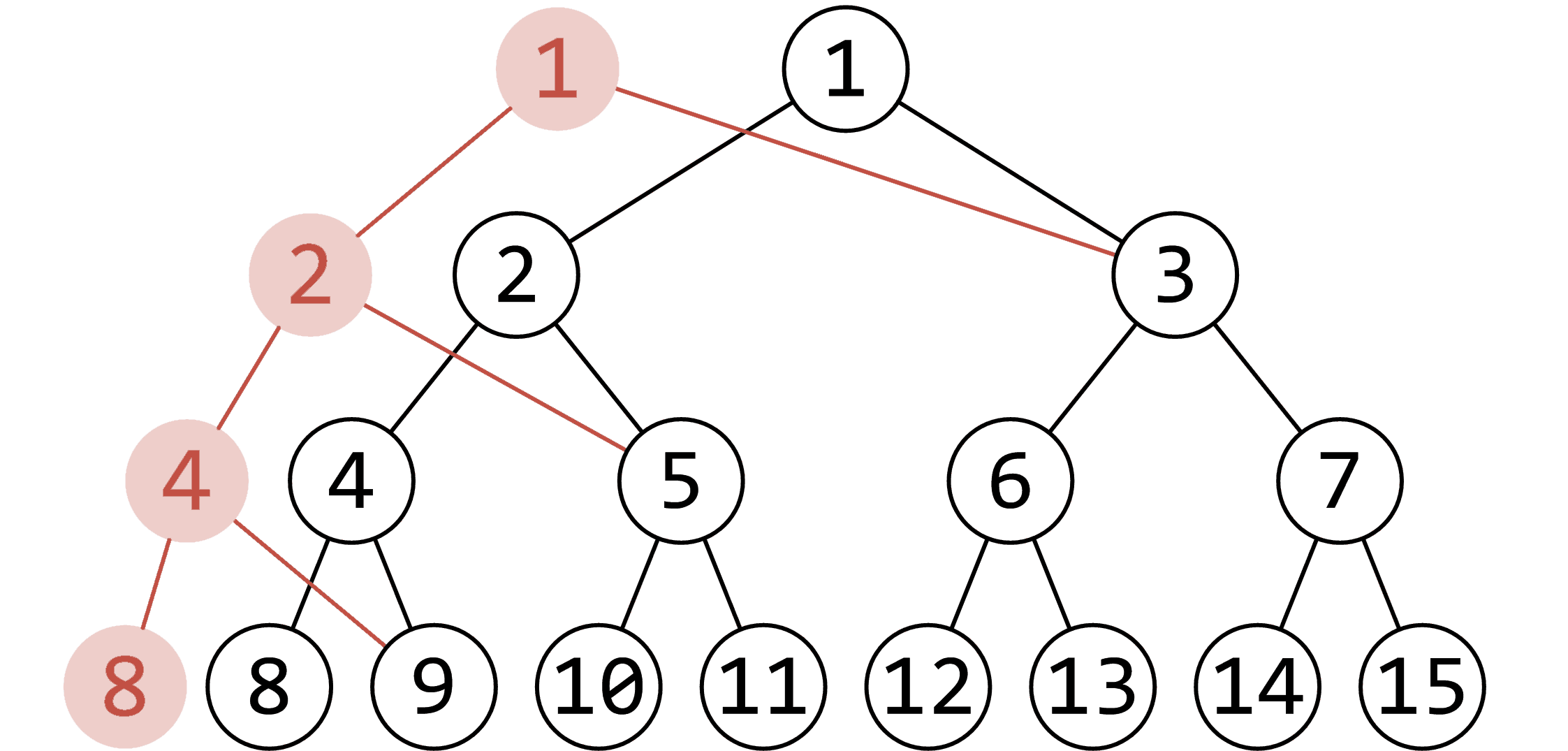
并不是很难，使用动态开点，用结构体存一下新开出的左右儿子编号，递归访问。每次修改的时候，新建一个节点并复制原节点信息，然后对于新的节点做修改，这样就可以保存历史版本。由于每次修改增加的点的数量不超过 logn 级别，所以单次修改的复杂度为 O(logn)。访问历史版本时，只要直接访问对应版本的根就可以啦。

#include<bits/stdc++.h>
using namespace std;
const int N = 1000000 + 10;
int n,m,tot;
struct Seg
{
    int l,r,val;
} tree[32*N];
int root[32*N];
int a[N];
int create(int p)
{
	tot++;
	tree[tot] = tree[p];
	return tot;
}
int build(int p,int l,int r)
{
	p = ++tot;
	if(l == r)
	{
		tree[p].val = a[l];
		return p;
	}
	int mid = (l + r) >> 1;
	tree[p].l = build(tree[p].l,l,mid);
	tree[p].r = build(tree[p].r,mid + 1,r);
	return p; 
}
int modify(int p,int l,int r,int x,int v)
{
	p = create(p);
	if(l == r)
	{
		tree[p].val = v;
		return p;
	}
	int mid = (l + r) >> 1;
	if(x <= mid) tree[p].l = modify(tree[p].l,l,mid,x,v);
	else tree[p].r = modify(tree[p].r,mid + 1,r,x,v);
	return p;
}
int query(int p,int l,int r,int x)
{
	if(l == r) return tree[p].val;
	int mid = (l + r) >> 1;
	if(x <= mid) return query(tree[p].l,l,mid,x);
	else return query(tree[p].r,mid + 1,r,x);
}
signed main()
{
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
	root[0] = build(0,1,n);
	for(int i = 1;i <= m;i++)
	{
		int rt,opt,x,v;
		scanf("%d%d%d",&rt,&opt,&x);
		if(opt == 1)
		{
			scanf("%d",&v);
			root[i] = modify(root[rt],1,n,x,v);
		}
		else
		{
			printf("%d\n",query(root[rt],1,n,x));
			root[i] = root[rt];
		}
	}
	return 0;
}

主席树

主席树的全称是可持久化权值线段树，解决的经典问题就是静态区间第 \(k\) 大问题。
传送门：主席树
对于这个问题，我们考虑一个一个的插入原序列的点，建成一棵主席树（跟可持久化线段树类似），然后利用差分的思想，把区间 \([l,r]\) 的信息转换为 \([1,r]-[1,l]\)。查询的时候和普通权值线段树一样，利用线段树自身的性质向下二分递归即可。

#include<bits/stdc++.h>
using namespace std;
const int N = 200000 + 10;
struct Seg
{
	int l,r,val;
} tree[32*N];
int root[32*N],a[N],t[N];
int n,m,len,tot;
int build(int p,int l,int r)
{
	p = ++tot;
	if(l == r) return p;
	int mid = (l + r) >> 1;
	tree[p].l = build(tree[p].l,l,mid);
	tree[p].r = build(tree[p].r,mid + 1,r);
	return p;
}
int create(int p)
{
	tot++;
	tree[tot] = tree[p];
	tree[tot].val++;
	return tot; 
}
int modify(int p,int l,int r,int x)
{
	p = create(p);
	if(l == r) return p;
	int mid = (l + r) >> 1;
	if(x <= mid) tree[p].l = modify(tree[p].l,l,mid,x);
	else tree[p].r = modify(tree[p].r,mid + 1,r,x);
	return p;
}
int query(int x,int y,int l,int r,int k)
{
	int rnk = tree[tree[y].l].val - tree[tree[x].l].val;
	if(l == r) return t[l];
	int mid = (l + r) >> 1;
	if(k <= rnk) return query(tree[x].l,tree[y].l,l,mid,k); 
	else return query(tree[x].r,tree[y].r,mid + 1,r,k - rnk);
}
signed main()
{
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n;i++)
	{
		scanf("%d",&a[i]);
		t[i] = a[i];
	}
	sort(t + 1,t + n + 1);
	len = unique(t + 1,t + n + 1) - t - 1;
	root[0] = build(0,1,len);
	for(int i = 1;i <= n;i++)
	{
		int cur = lower_bound(t + 1,t + len + 1,a[i]) - t;
		root[i] = modify(root[i-1],1,len,cur);
	}
	for(int i = 1;i <= m;i++)
	{
		int l,r,k;
		scanf("%d%d%d",&l,&r,&k);
		printf("%d\n",query(root[l-1],root[r],1,len,k));
	} 
	return 0;
}

据说主席树还可以简单实现可持久化并查集，蒟蒻以后学习啦。