HappyNewYear(感谢范展诚学长的分享)
顺十字在此祝各位新年快乐
A - 顺
题目描述

输入描述

输出描述

样例输入
7
abacaba
abc
cccba
acb
dbsic
bac
abracadabra
abc
dddddddddddd
cba
bbc
abc
ac
abc
样例输出
aaaacbb
abccc
bcdis
aaaaacbbdrr
dddddddddddd
bbc
ac
思路
S只有6种可能:abc, acb, bac, bca, cab, cba
只需要判断T是不是abc和S中有无a。
如果T不是abc,只要将 S 按顺序排列,那么不可能出现T的情况,因为a永远在前,不可能与b,c重复,也不可能与bc重复。
如果T是abc,分两种情况
- S中有
a,那么需要排序并且bc调换顺序输出; - S中没有
a,排序按顺序输出就好。
代码
int n;
string s,t;
int sum[30]; //sum[i]存第i个字母的数量
void init()
{
for(int i = 0; i < 29; i++) sum[i] = 0;
cin >> s >> t;
}
void solve() //solve只管abc的输出
{
for(int i = 0; i < s.size(); i++) sum[s[i]-'a']++;
bool flag = false;
if(sum[0]) flag = true; //判断S串中是否有a存在
while(sum[0]--) printf("a"); //无论如何a都优先输出
if(t[0] != 'a' || (!flag&&t[0] == 'a')) return; //T串首字母不为a或首字母为a但S串没a,按顺序输出就好
if(t[1] == 'b') //否则如果首字母为a,如果是abc,就先输出acb再输出剩下的,否则按顺序输出
{
while(sum[2]--) printf("c");
while(sum[1]--) printf("b");
}
}
int main()
{
int t;
cin >> t;
while(t--)
{
init(),
solve();
for(int i = 0; i < 29; i++) //剩下的字母输出
{
while(sum[i]>0) printf("%c",'a'+i), sum[i]--;
}
printf("\n");
}
return 0;
}
B - 十
题目描述

输入描述

输出描述

样例输入
6
18
63
73
91
438
122690412
样例输出
6 9 3
21 39 3
29 43 1
49 35 7
146 219 73
28622 122661788 2
思路
可以想到将 n 拆成两个互质且和为n-1的数,第三个数为 c ,由于n >= 10这样的组合一定存在
代码
int n;
void init()
{
scanf("%d",&n);
}
void solve()
{
n--;
int a,b;
if(n&1) //奇数
{
printf("%d %d ",n/2,n-n/2);
}
else //偶数
{
a = n/2+1, b = n/2-1;
while(__gcd(a,b) != 1)
{
a++,b--;
}
printf("%d %d ",a,b);
}
printf("1\n");
}
int main()
{
int t;
cin >> t;
while(t--)
init(),
solve();
return 0;
}
C - 字
题目描述

输入描述

输出描述

样例输入
4
2
1 7
3
1 5 4
4
12345678 87654321 20211218 23571113
9
1 2 3 4 18 19 5 6 7
样例输出
1
-1
4
2
思路
思考这一操作的性质,容易得出对于任意数
- 如果为
偶数,可以变成 0 ~ n / 2 - 1 - 如果为奇数,可以变成
0 ~ n / 2
因此,越大的数字可以变化的范围越大,可以得出一个贪心的想法:
- 对于每个数n,最大的时候是不进行操作,还是 n 本身,如果 n 本身已经被其他数字变了,则存起来用来变其他数字,又因为越大的数字可以变化的范围越大,因此将数字存起来后从小到大排序,对 1 ~ n 之间从小到大的缺口一一对应,如果都可以变输出变的次数,否则输出 -1
代码
int a[100010];
int n;
vector<int> num1,num2;
bool st[100010]; //用来标记1~n哪些数被已经有了
void init()
{
num1.clear();
num2.clear();
cin >> n;
for(int i = 1; i <= n; i++) scanf("%d",&a[i]), st[i] = false; //多组输出,因此要将st[i]恢复到false,避免之前的影响
sort(a+1,a+1+n); //数字排序
for(int i = 1; i <= n; i++)
{
if(a[i] <= n && !st[a[i]]) //如果一个数字不用变,是最优的情况
{
st[a[i]] = true;
}
else
num2.push_back(a[i]); //如果这个数已经有了,则存起来用来变其他数字
}
for(int i = 1; i <= n; i++)
{
if(!st[i])
num1.push_back(i); //将还没有的数字存到num1里
}
}
int solve()
{
int ans = 0;
int len = num1.size()-1;
for(int i = len; i >= 0; i--) //但凡有一次变不成,则返回-1
{
if(num2[i]&1) //如果为奇数,可以变成0~n/2
{
if(num1[i] <= num2[i]/2) ans++;
else return -1;
}
else //如果为偶数,可以变成0~n/2-1
{
if(num1[i] <= num2[i]/2-1) ans++;
else return -1;
}
}
return ans;
}
int main()
{
int t;
cin >> t;
while(t--)
init(),
printf("%d\n",solve());
return 0;
}
D - 在
题目描述

输入描述

输出描述

样例输入
9 14
1 2 4
2 3 8
3 4 7
4 5 9
5 6 10
6 7 2
7 8 1
8 9 7
2 8 11
3 9 2
7 9 6
3 6 4
4 6 14
1 8 8
样例输出
37
思路
求最小生成树的板子题,学会了直接a掉就行
代码1(kruskal)
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e3 + 10;
int n, m;
int p[N];
struct Node {
int s, e;
int w;
}edge[M];
int find(int x) {
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++) p[i] = i;
for (int i = 1; i <= m; i ++) cin >> edge[i].s >> edge[i].e >> edge[i].w;
sort(edge + 1, edge + m + 1, [](Node a, Node b) {
return a.w < b.w;
});
int ans = 0;
for (int i = 1; i <= m; i ++) {
int pa = find(edge[i].s), pb = find(edge[i].e), w = edge[i].w;
if (pa == pb) continue;
p[pa] = pb;
ans += w;
}
cout << ans << endl;
return 0;
}
代码2(prim)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 510, M = 1e6 + 10;
int n, m;
int dist[N];
int g[N][N];
bool st[N];
int Prim(){
int re = 0;
memset(dist, 0x3f, sizeof dist);
//dist[1] = 0;
for(int i = 0; i < n; i++){
int t = -1;
for(int j = 1; j <= n; j++)
if(!st[j] && (t == -1 || dist[j] < dist[t]))
t = j;
if(i && dist[t] == 0x3f3f3f3f) return 0x3f3f3f3f;
if(i) re += dist[t];
//printf("%d %d\n", t, re);
for(int j = 1; j <= n; j++)
dist[j] = min(dist[j], g[t][j]);
st[t] = true;
}
return re;
}
int main(){
memset(g, 0x3f, sizeof g);
scanf("%d%d", &n, &m);
for(int i = 0; i < m; i++){
int a, b, w;
scanf("%d%d%d", &a, &b, &w);
g[a][b] = min(g[a][b], w);
g[b][a] = min(g[b][a], w);
}
int t = Prim();
if(t == 0x3f3f3f3f) puts("impossible");
else printf("%d\n", t);
return 0;
}
E - 此
题目描述

输入描述

输出描述

样例输入
3 3
1
2
3
2 1
3 2
4 3
样例输出
6
思路
贪心+优先队列
首先
- 将兔子血量从大到小排序
- 箭按伤害从大到小排序
明显 要杀死兔子i
使用伤害 >= b[i] 且消耗Q币最少的箭 是最优方案
每次将伤害>=b[i]的箭消耗的Qb放进小顶堆中,然后取出最小值
代码
#define ll long long
#define ull unsigned long long
#define pii pair<int,int>
#define INF 1000000007
const int N=50000+5;
int b[N];
pii arrow[N];
ll slove(int n,int m){
sort(b,b+n,greater<int>());
sort(arrow,arrow+m,greater<pii>());
priority_queue<int,vector<int>,greater<int> >que;
int index=0;
ll cost=0;
for(int i=0;i<n;++i){
while(index<m&&arrow[index].first>=b[i])
que.push(arrow[index++].second);
if(que.empty())
return -1;
cost+=que.top();
que.pop();
}
return cost;
}
int main()
{
//freopen("/home/lu/文档/r.txt","r",stdin);
//freopen("/home/lu/文档/w.txt","w",stdout);
int n,m;
scanf("%d%d",&n,&m);
for(int i=0;i<n;++i)
scanf("%d",b+i);
for(int i=0;i<m;++i)
scanf("%d%d",&arrow[i].first,&arrow[i].second);
if(m<n)
printf("No Solution\n");
else{
ll res=slove(n,m);
if(res==-1)
printf("No Solution\n");
else
printf("%lld\n",res);
}
return 0;
}
F - 祝
题目描述

输入描述

输出描述

样例输入
4 11
8.02 7.43 4.57 5.39
样例输出
2.01
思路
这是一个裸二分模板题目,不过这是浮点数二分,需要处理精度问题,周六讲了二分思路
练二分题可以去acwing或者洛谷刷一刷
二分每一截的长度,判断能不能取到k段…….
代码
const int N = 1e4+10;
int n,k;
double a[N];
bool check (double mid)
{
int sum = 0;
for(int i = 0; i < n; i++)
sum += (int)(a[i]/mid);
if(sum >= k) return true;
return false;
}
void init()
{
scanf("%d%d",&n,&k);
}
double solve()
{
double l,r,mid;
for(int i = 0;i < n; i++)
{
scanf("%lf",&a[i]);
r += a[i];
}
r = 10000, l = 0.0, mid;
while(fabs(r - l) > 0.00001)
{
mid = (l+r)/2;
if(check(mid)) l = mid; //如果符合说明答案小了,往上提高
else r = mid; //答案大了,往下
}
mid = (mid*1000+0.5);
mid /= 1000;
return mid;
}
int main()
{
init();
printf("%.2lf",solve());
return 0;
}
G - 各
题目描述

输入描述

输出描述

样例输入
4
样例输出
3
思路
- 每个质数必须询问一次,
- 由于非质数是由质数相乘得到的,因此不用询问。
- 但是有特殊情况,就是合数有多个相同的质因子,比如说n=4,4个数1、2、3、4,由于4是22得到的,你不能只询问2,还要询问22。因此,先找出小于等于n的质数,然后统计此质数有多少个幂次小于等于n,举例说明,n=5时,质数为2、3、5,2 ^ 1 < 5,2 ^ 2 < 5,3 ^ 1 < 5,5 ^ 1 < 5,因此答案为4
因为n很小,可以用很暴力的方法跑过去,不是很需要考虑时间复杂度,更简单的方法还有从数论角度考虑的
代码
const int N=1005;
int prime[N+1];
//质数筛
void solve(int n)
{
prime[0]=prime[1]=1;
for(int i=2;i<=n;i++)
if(!prime[i])
{
for(int j=i+i;j<=n;j+=i)
prime[j]=1;
}
}
int main()
{
solve(N);
int n,ans=0;
scanf("%d",&n);
for(int i=1;i<=n;i++)
if(!prime[i])//如果i是质数
{
for(int j=i;j<=n;j*=i)//质数i的幂次需要各询问一次
ans++;
}
printf("%d\n",ans);
return 0;
}
H - 位
题目描述

输入描述
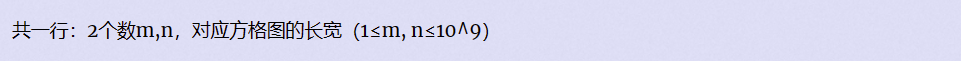
输出描述

样例输入
8 6
样例输出
12
思路
首先第一时间可以想到,如果从左上角走到右下角,保底会切一个长+宽的方格,但样例就可以发现14比6+8小,是因为有些格子同时走x方向和y方向
可以自己多试几组找规律,很容易发现,比长和宽少的格子就是恰好穿过格子的顶点的,而这样的格子为gcd(x,y),xy为长和宽,因此答案为x+y-gcd(x,y)
代码
int gcd(int a,int b){
return b ? gcd(b, a% b) : a;
}
int main()
{
int m,n,cnt;
cin >> m >> n;
if(m == n)
cnt = m;
else{
cnt = (m + n) - gcd(m,n);
}
cout << cnt;
return 0;
}
I - 新
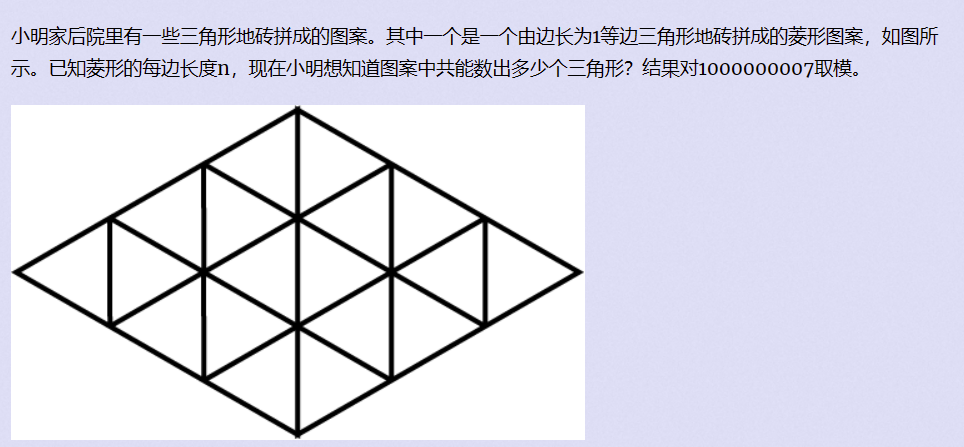
题目描述
输入描述

输出描述

样例输入
3
样例输出
28
思路
可以发现,每个三角形都由一个竖线和两个斜线组成,因此我们可以观察每一条竖线,统计其对答案的贡献
对于最左边的竖线,可以观察到可组成两个三角形,第二条竖线:大小为1的三角形4个,大小为2的三角形2个,第三个竖线:大小1三角形6个,大小2三角形4个,大小3三角形2个……可以发现对于每一个竖线,可以用一个等差数列求和公式为(2+2i)i/2,化简为i+i^2,共有2*n+1条竖线,用此公式可以O(n)计算答案,而vj上挂的题没写n的取值范围,去原网站看实际取值范围是1~1e9,因此O(n)还是会TLE,还需要再化简,化简过程如下:
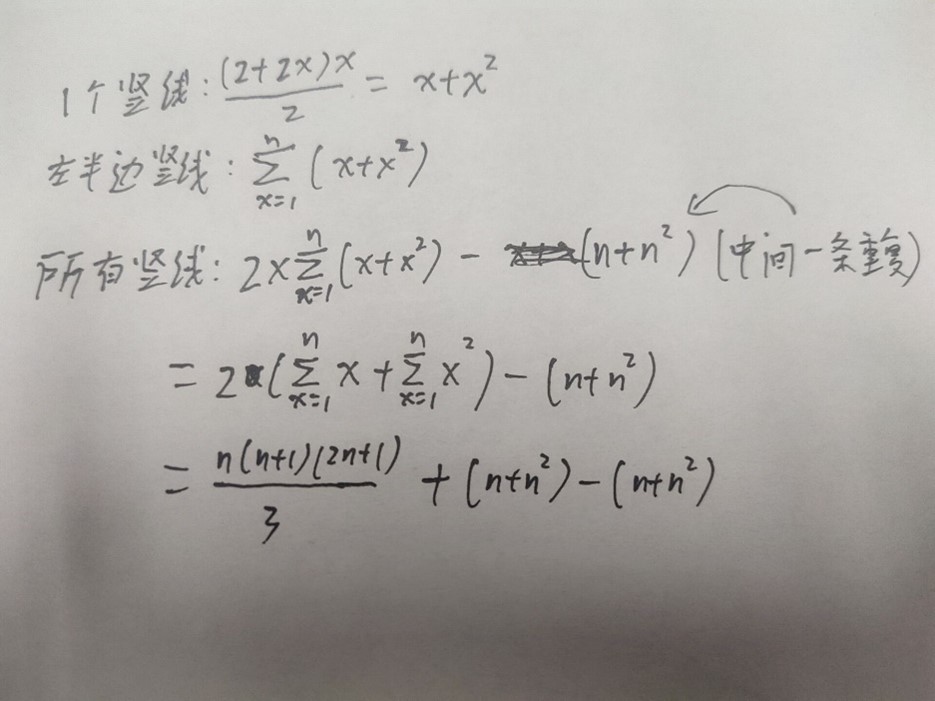
因此最后答案就是n(n+1)(2n+1)/3,可以O(1)出答案
考虑到n最大为1e9,直接乘起来会爆longlong,又因为有取模和除法同时存在的问题,因此有两种写法:
代码1
typedef long long ll;
const int mod = 1e9 + 7;
int main()
{
ll n;
cin>>n;
ll a = n, b = n+1, c = 2*n+1;
if(a % 3 == 0) a /= 3;
else if(b % 3 == 0) b /= 3;
else c /= 3;
ll ans = (a*b)%mod;
ans = (ans*c)%mod;
cout << ans;
return 0;
}
代码2(感谢张纭昌学长的分享)
typedef long long ll;
const int mod = 1e9 + 7;
ll qmi(ll a, ll b)
{
ll res = 1;
while(b)
{
if(b&1) res = res * a % mod;
b >>= 1;
a = a * a % mod;
}
return res;
}
int main()
{
ll n;
cin>>n;
cout<<((n * (n+1)%mod)*(2*n+1) % mod) % mod * qmi(3,mod-2) % mod;
return 0;
}
J - 年
题目描述

输入描述

输出描述

样例输入
样例输出
思路
用线性筛筛一下,因为n取值范围在1e6,保守起见开一个1e6+1000的bool类型的数组记录哪个是质数,顺便记录一下该质数是第几个质数,从大于n的地方直接找就行,时间复杂度O(n)
代码(感谢杜新富同学的分享)
const int N = 1e6 + 10;
int a[N]={1,1,0};
int main()
{
int n, i, j, k=0;
cin >> n;
for ( i = 2; i < N; i ++ )
{
if (!a[i])
{
k ++;
if (!a[k] && i >= n)
{
cout << i;
break;
}
for ( j = i + i; j < N; j += i )
{
a[j]=1;
}
}
}
return 0;
}
K - 快
题目描述

输入描述

输出描述

样例输入
6
5 5
10 1
2 3
0 0
17 2
1000000000 1000000000
样例输出
2
1
1
0
2
500000000
思路
因为一个队伍最坏只能是1个程序员配3个数学家,或者3个程序员配一个数学家,因此如果出现a*3 <= b 或者b*3 <= a,直接输出min(a,b)即可,否则说明他们肯定能组成(n+m)/4队
代码
ll a,b;
void init()
{
cin >> a >> b;
}
void solve()
{
ll ans = 0;
if(a*3 <= b || b*3 <= a) ans = min(a,b);
else ans = (a+b)/4;
cout << ans << endl;
}
int main()
{
int t;
cin >> t;
while(t--)
init(),
solve();
return 0;
}
L - 乐
题目描述

输入描述

输出描述

样例输入
5
2 2
1 2
3 4
4 3
1 3 1
3 1 1
1 2 2
1 1 3
2 3
5 3 4
2 5 1
4 2
7 9
8 1
9 6
10 8
2 4
6 5 2 1
7 9 7 2
样例输出
3
2
4
8
2
思路1
- 当m<=n-1时 可去全部商店对每个人都取最大值即可
- 当m>n-1时,只能去n-1家商店,所以有两个人的礼物在同一家商店,我们暴力枚举哪两个人在哪家商店,由 数据范围 可得 n最大是sqrt(1e5) 时间复杂度o(n^3) 大概是3e7 可以过
代码1
const int N=1e5+10;
vector<int> a[N],b[N];//不定长数组
// a横着 b竖着
int main()
{
int T;
cin>>T;
while(T--)
{
int m,n;
scanf("%d%d",&m,&n);
for(int i=1;i<=n;i++)
b[i].clear();
for(int i=1;i<=m;i++)
a[i].clear();
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
int x;
scanf("%d",&x);
a[i].push_back(x);
b[j].push_back(x);
}
}
for(int i=1;i<=n;i++)
sort(b[i].begin(),b[i].end(),greater<int>());
if(m<=n-1)
{
int ans=1e9+10;
for(int i=1;i<=n;i++)
ans=min(ans,b[i][0]);
printf("%d\n",ans);
}
/*
m>n-1 m*n<=1e5
n<=sqrt(1e5)
*/
else
{
int ans=0;
for(int i=1;i<=n;i++)//i与j选择在同一行
{
for(int j=i+1;j<=n;j++)
{
int res=1e9+10;
for(int k=1;k<=n;k++)
{
if(k==i||k==j) continue;
res=min(res,b[k][0]);
}
int op=0;
for(int k=1;k<=m;k++)//两个元素选在了哪一行
{
op=max(op,min(a[k][i-1],a[k][j-1]));
}
res=min(res,op);
ans=max(ans,res);
}
}
printf("%d\n",ans);
}
}
return 0;
}
思路2
我们可以二分最终的答案, 然后去查看是否有一个商店可以买到两个及以上的人的礼物, 如果可以就说明这个答案是可以被满足的
当然也要注意可能有一个商店买不到合适的礼物
代码2
int n, m;
vector<vector<int>> a;
bool st[100010];
bool check(int u) {
memset(st, false, sizeof st);
bool flag = false;
for (int i = 0; i < m; i ++) {
int cnt = 0;
for (int j = 0; j < n; j ++) {
if (a[j][i] >= u) {
cnt ++;
if (st[j]) flag = true;
st[j] = true;
}
}
if (cnt == 0) return false;
}
return flag;
}
int main() {
int T;
cin >> T;
while (T --) {
cin >> n >> m;
a.clear();
for (int i = 1; i <= n; i ++) {
vector<int> b;
for (int j = 1; j <= m; j ++) {
int x;
cin >> x;
b.push_back(x);
}
a.push_back(b);
}
int l = 1, r = 1e9 + 1;
while (r > l) {
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
cout << l << endl;
}
return 0;
}
总结
这周的训练赛确实难了一点,但也有很多人做的很好,学算法有一个入门的过程,基础打好以后学起来就很快了,各位加油吧!
在力所能及范围内把能补的题都补掉,实在感觉难的就不要一道题死磕一两天,平时可以去codeforces, acwing,牛客,pat,洛谷之类的网站刷刷题练基础。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号