树套树类试题思路记录
[ZJOI2013]K大数查询
如果不区分这n个集合,即将这些集合合并起来,那就是动态整体第kth。将数据离散化后按点值建立一颗权值主席树维护即可。
现在区分出了n个集合,插入和查询操作都要在指定 \([l,r]\) 区间内操作,我们不妨令原有的权值主席树的每一个节点都维护一个线段树,来维护n个集合。
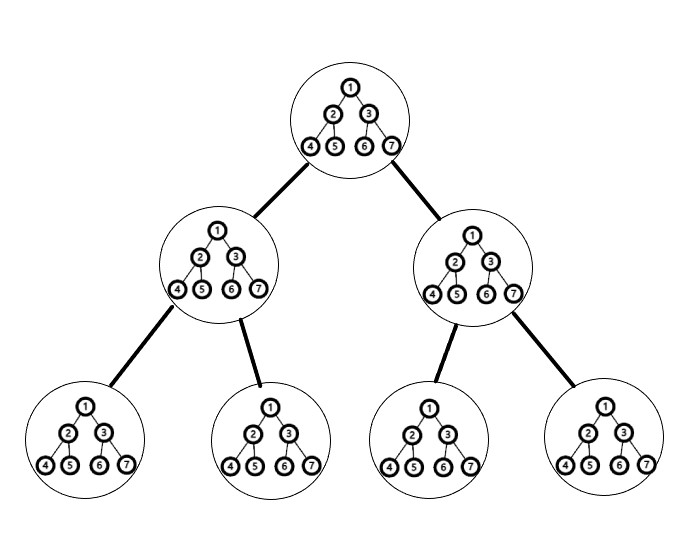
考虑到最坏情况,要建立 \(n\) 数量级颗线段树,如果全部建满的话空间复杂度 \(O(n^2logn)\),无法接受。可以动态开点地建树,只有用到某个点再开这个点,节省空间。这样最坏的情况每次询问都新建点,空间占用 \(log^2n\),总的空间复杂度 \(O(mlog^2n)\),可以接受。
code
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
inline ll read(){
ll w=1,q=0;char ch=' ';
while(ch!='-' && (ch<'0' || ch>'9')) ch=getchar();
if(ch=='-') w=-1,ch=getchar();
while(ch<='9' && ch>='0') q=q*10+ch-'0',ch=getchar();
return w*q;
}
const int MAXN = 5e4+5,MAXQ = 2e7+25;
ll n,m,root[MAXN<<1],X[MAXN],cntn;
ll op[MAXN],L[MAXN],R[MAXN],C[MAXN];
struct Dynamic_Segment_Tree{
#define mid ((l+r)>>1)
ll val[MAXQ],L[MAXQ],R[MAXQ],tag[MAXQ],cnt;
inline void push_down(int l,int r,int p){
if(tag[p]==0) return;
if(!L[p]) L[p]=++cnt;
if(!R[p]) R[p]=++cnt;
val[L[p]]+=tag[p]*(mid-l+1),val[R[p]]+=tag[p]*(r-mid);
tag[L[p]]+=tag[p],tag[R[p]]+=tag[p],tag[p]=0;return;
}
void add(int l,int r,ll &p,int a,int b){
if(!p) p=++cnt;
if(a<=l && r<=b){val[p]+=r-l+1,tag[p]++;return;}
push_down(l,r,p);
if(a<=mid) add(l,mid,L[p],a,b);
if(b>mid) add(mid+1,r,R[p],a,b);
val[p]=val[L[p]]+val[R[p]];return;
}
ll query(int l,int r,ll &p,int a,int b){
if(!p) p=++cnt;
if(a<=l && r<=b) return val[p];
push_down(l,r,p);int temp=0;
if(a<=mid) temp+=query(l,mid,L[p],a,b);
if(b>mid) temp+=query(mid+1,r,R[p],a,b);
return temp;
}
}tret;
//外层权值树
#define mid ((l+r)>>1)
void modify(int l,int r,int p,int a,int b,int c){
tret.add(1,n,root[p],a,b);
if(l==r) return;
if(c<=mid) modify(l,mid,p*2,a,b,c);
else modify(mid+1,r,p*2+1,a,b,c);
return;
}
ll query(int l,int r,int p,int a,int b,int c){
if(l==r) return l;
ll sum=tret.query(1,n,root[p*2+1],a,b);
if(sum<c) return query(l,mid,p*2,a,b,c-sum);
else return query(mid+1,r,p*2+1,a,b,c);
}
signed main(){
n=read(),m=read();
//离散化
for(int i=1; i<=m; i++){
op[i]=read(),L[i]=read(),R[i]=read(),C[i]=read();
if(op[i]==1) X[++cntn]=C[i];
}
sort(X+1,X+cntn+1);int len=unique(X+1,X+cntn+1)-X-1;
for(int i=1; i<=m; i++){
if(op[i]==1) C[i]=lower_bound(X+1,X+len+1,C[i])-X;
}
//查询
for(int i=1; i<=m; i++){
if(op[i]==1){
modify(1,len,1,L[i],R[i],C[i]);
}else{
printf("%lld\n",X[query(1,len,1,L[i],R[i],C[i])]);
}
}
}
Dynamic Rankings
如果没有C操作,即查询静态区间第kth,对每个点及其前缀建一颗权值树,那么任意一段区间可以表示为两颗树相减。可以用主席树维护。
加上C操作后,每一次修改x位置的值都需要牵动一同修改第x颗到第n颗权值树,复杂度难以接受。由于每一颗权值树维护的是一个前缀,我们想到树状数组的操作,让第x颗树不再维护区间 \([1,x]\),而是维护 \([x-lowbit(x)+1,x]\) 的区间。每次修改都是稳定地修改 \(logn\) 颗树,这样总体时间复杂度 \(O(nlog^2n)\),可以接受。
code
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int q=0;char ch=' ';
while(ch<'0' || ch>'9') ch=getchar();
while(ch<='9' && ch>='0') q=q*10+ch-'0',ch=getchar();
return q;
}
const int MAXN = 5e5+25;
int n,m,cnt,len,arr[MAXN],X[MAXN<<1];
int cntl,cntr,rot[MAXN],sumtre[2][205];
struct Question{
char op;
int a,b,k;
}Q[MAXN];
struct Persistable_Segment_Tree{
int l,r,val;
}tre[MAXN*40];
void change(int l,int r,int &p,int pos,int k){
if(!p) p=++cnt;
tre[p].val+=k;
if(l==r) return;
int mid=(l+r)>>1;
if(pos<=mid) change(l,mid,tre[p].l,pos,k);
else change(mid+1,r,tre[p].r,pos,k);
}
inline void pre_change(int x,int k){
int pos=lower_bound(X+1,X+len+1,arr[x])-X;
for(int i=x; i<=n; i+=i&-i) change(1,len,rot[i],pos,k);
return;
}
int query(int l,int r,int k){
if(l==r) return l;
int mid=(l+r)>>1,sum=0;
for(int i=1; i<=cntr; i++) sum+=tre[tre[sumtre[1][i]].l].val;
for(int i=1; i<=cntl; i++) sum-=tre[tre[sumtre[0][i]].l].val;
if(k<=sum){
for(int i=1; i<=cntr; i++) sumtre[1][i]=tre[sumtre[1][i]].l;
for(int i=1; i<=cntl; i++) sumtre[0][i]=tre[sumtre[0][i]].l;
return query(l,mid,k);
}else{
for(int i=1; i<=cntr; i++) sumtre[1][i]=tre[sumtre[1][i]].r;
for(int i=1; i<=cntl; i++) sumtre[0][i]=tre[sumtre[0][i]].r;
return query(mid+1,r,k-sum);
}
}
inline int pre_query(int a,int b,int k){
memset(sumtre,0,sizeof(sumtre));
cntl=cntr=0;
for(int i=a-1; i; i-=(i&-i)) sumtre[0][++cntl]=rot[i];
for(int i=b; i; i-=(i&-i)) sumtre[1][++cntr]=rot[i];
return query(1,len,k);
}
signed main(){
ios::sync_with_stdio(false);
cin>>n>>m;
for(int i=1; i<=n; i++) cin>>arr[i],X[++len]=arr[i];
for(int i=1; i<=m; i++){
cin>>Q[i].op;
if(Q[i].op=='Q') cin>>Q[i].a>>Q[i].b>>Q[i].k;
else cin>>Q[i].a>>Q[i].b,X[++len]=Q[i].b;
}
sort(X+1,X+len+1);
len=unique(X+1,X+len+1)-X-1;
for(int i=1; i<=n; i++) pre_change(i,1);
for(int i=1; i<=m; i++){
if(Q[i].op=='C'){
pre_change(Q[i].a,-1),arr[Q[i].a]=Q[i].b;
pre_change(Q[i].a,1);
}else{
printf("%d\n",X[pre_query(Q[i].a,Q[i].b,Q[i].k)]);
}
}
return 0;
}
[CQOI2011]动态逆序对
由于要单点修改,思考一个点对逆序对数量的贡献。即位置在该点之前且值大于该点,和位置在该点之后且值小于该点的点的数量。用权值树可以维护。
同上题类似,第x颗权值树维护的不是区间 \([1,x]\),而是 \([x-lowbit(x)+1,x]\)。
code
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;
inline ll read(){
ll w=1,q=0;char ch=' ';
while(ch!='-' && (ch<'0' || ch>'9')) ch=getchar();
if(ch=='-') w=-1,ch=getchar();
while(ch<='9' && ch>='0') q=q*10+ch-'0',ch=getchar();
return q;
}
const ll MAXN = 1e5+5;
ll n,m,a[MAXN],root[MAXN],pos[MAXN],ans;
//[CQOI2011]动态逆序对
//i<j && ai>aj
struct Persistable_Segment_Tree{
#define mid ((l+r)>>1)
ll val[MAXN*400],L[MAXN*400],R[MAXN*400],cnt;
void modify(ll l,ll r,ll &p,ll pos,ll k){
if(!p){p=++cnt;}if(l==r){val[p]+=k;return;}
if(!L[p]) L[p]=++cnt;
if(!R[p]) R[p]=++cnt;
if(pos<=mid) modify(l,mid,L[p],pos,k);
else modify(mid+1,r,R[p],pos,k);
val[p]=val[L[p]]+val[R[p]];return;
}
ll query_left(ll l,ll r,ll p,ll pos){
if(l==r) return (pos==l?val[p]:0);
if(pos<=mid) return (val[R[p]]+query_left(l,mid,L[p],pos));
else return query_left(mid+1,r,R[p],pos);
}
ll query_right(ll l,ll r,ll p,ll pos){
if(l==r) return (pos==l?val[p]:0);
if(pos>mid) return (val[L[p]]+query_right(mid+1,r,R[p],pos));
else return query_right(l,mid,L[p],pos);
}
}tret;
inline ll lowbit(ll x){return x&-x;}
inline void change(ll x,ll k,ll pos){while(x<=n){tret.modify(1,n,root[x],pos,k),x+=lowbit(x);}}
inline ll sum_left(ll x,ll pos){ll ans=0;while(x>=1){ans+=tret.query_left(1,n,root[x],pos+1),x-=lowbit(x);}return ans;}
inline ll sum_right(ll x,ll pos){ll ans=0;while(x>=1){ans+=tret.query_right(1,n,root[x],pos-1),x-=lowbit(x);}return ans;}
signed main(){
n=read(),m=read();
for(ll i=1; i<=n; i++){
a[i]=read();pos[a[i]]=i;
change(pos[a[i]],1,a[i]);
}
for(ll i=1; i<=n; i++){
ans+=sum_left(pos[a[i]],a[i]);
}
for(ll i=1; i<=m; i++){
ll x=read();
printf("%lld\n",ans);
ans-=sum_left(pos[x],x);
ans-=sum_right(n,x)-sum_right(pos[x]-1,x);
change(pos[x],-1,x);
}
}
[国家集训队]排队
统计动态逆序对,与上题相似。
发现交换 \((a,b)\) 只会影响 \([a,b]\) 区间的逆序对个数,那就统计改变前和改变后 \([a,b]\) 区间的逆序对个数即可。
code
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
inline int read(){
int q=0;char ch=' ';
while(ch<'0' || ch>'9') ch=getchar();
while(ch<='9' && ch>='0') q=q*10+ch-'0',ch=getchar();
return q;
}
const int MAXN = 2e4+5;
int n,m,len,arr[MAXN],root[MAXN],X[MAXN],ans;
struct Dynamic_Segment_Tree{
#define mid ((l+r)>>1)
int cnt,L[MAXN*400],R[MAXN*400],val[MAXN*400];
void modify(int l,int r,int &p,int pos,int k){
if(!p) p=++cnt;
if(l==r){val[p]+=k;return;}
if(pos<=mid) modify(l,mid,L[p],pos,k);
if(pos>mid) modify(mid+1,r,R[p],pos,k);
val[p]=val[L[p]]+val[R[p]];return;
}
int left_query(int l,int r,int p,int pos){//[p1,p2]区间小于pos的数量
if(!p) return 0;
if(l==r) return (l==pos?val[p]:0);
if(pos<=mid) return left_query(l,mid,L[p],pos);
if(pos>mid) return (val[L[p]]+left_query(mid+1,r,R[p],pos));
}
int right_query(int l,int r,int p,int pos){
if(!p) return 0;
if(l==r) return (l==pos?val[p]:0);
if(pos<=mid) return (val[R[p]]+right_query(l,mid,L[p],pos));
if(pos>mid) return right_query(mid+1,r,R[p],pos);
}
}tret;
inline int lowbit(int x){return x&-x;}
inline void add(int x,int k,int pos){while(x<=n){tret.modify(1,len,root[x],pos,k),x+=lowbit(x);}return;}
inline int sum_left(int x,int pos){int ans=0;while(x>=1){ans+=tret.left_query(1,len,root[x],pos-1),x-=lowbit(x);}return ans;}
inline int sum_right(int x,int pos){int ans=0;while(x>=1){ans+=tret.right_query(1,len,root[x],pos+1),x-=lowbit(x);}return ans;}
signed main(){
n=read();
for(int i=1; i<=n; i++) X[i]=arr[i]=read();
sort(X+1,X+n+1);len=unique(X+1,X+n+1)-X-1;
for(int i=1; i<=n; i++) arr[i]=lower_bound(X+1,X+len+1,arr[i])-X;
for(int i=1; i<=n; i++) add(i,1,arr[i]);
for(int i=1; i<=n; i++) ans+=sum_right(i,arr[i]);
m=read();
printf("%d\n",ans);
for(int i=1; i<=m; i++){
int a=read(),b=read();
if(a>b) swap(a,b);
ans-=sum_right(b,arr[b])-sum_right(a-1,arr[b]),ans-=sum_left(b,arr[a])-sum_left(a,arr[a]);
if(arr[a]>arr[b]) ans++;
add(a,1,arr[b]),add(a,-1,arr[a]);add(b,1,arr[a]),add(b,-1,arr[b]),swap(arr[a],arr[b]);
ans+=sum_right(b,arr[b])-sum_right(a-1,arr[b]),ans+=sum_left(b,arr[a])-sum_left(a,arr[a]);
if(arr[a]>arr[b]) ans--;
printf("%d\n",ans);
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号