基础贪心集合
前言
贪心,顾名思义,就是只看眼前,思考问题的方式可能有些短视,但有些问题就是可以通过贪心求得最优解,问题在于如何贪心并且如何证明贪心能够求得最优解,后面通过几道例题简单点出基础贪心里得一些基础思路。
区间问题
题目链接1–区间取点
这题y总得证明我没法很好理解就不说了,说说我个人得理解,对于证明可能会比较不严谨,只是一个理解。
我们将每一个区间按照区间右端点进行排序,然后在每一个区间的右端点取点,如果这个点包含在其他区间内,那包含该点的其他区间就不用取点。
其实就是因为我是在右端点取的点,并且每个区间是按右端点排序的,当前区间的右端点一定小于等于下一个区间的右端点,只要当前区间的右端点尽可能长,就能够超过下一个区间的左端点,就可以达成多个区间点的共用,如果当前区间的右端点往左一些去点同样满足,那么右端点取点也肯定满足,而且可能包含的区间更多,因为区间是按照右端点排序的。
既然每个区间只要有一个点就行了,那么当我确定要在某一个区间内选择点时,为什么不将这个点尽量的延后从而使得更多的区间可以利用到它呢?
严格证明等以后想通了再补充把。
题目链接2–最大不相交区间数量
谁能想到上面这两题的代码竟然一模一样!!
明明第一题求的的最小点,第二题求得最大区间个数,我简单说一下我的理解:
第一题是在排除没有和其他区间有交集的区间外,找到区间的公用部分的个数。第二题是因为求的是最大不相交的区间个数,除去那些与其他区间没有任何交集的区间,如果任意几个区间有公共部分,那么一旦选了这几个区间的任意一个,其他几个区间都不能选,每一个区间的公共部分(区间取点最少个数的取点位置)都表示这一块公共部分涉及的区间只能取一个,所以在将取完与其他区间全无交集的区间后再加上公共区间的个数就是取得区间个数的最大值。如果这些区间的任意一个区间不取得到的就是比最大不相交区间数量小的数。
可以类比学校选课,使得选课数量最大的问题。
#include<iostream>
#include<vector>
#include<utility>
#include<algorithm>
using namespace std;
const int N = 1e5 + 5;
typedef pair<int, int> PII;
bool cmp(PII a, PII b) {
return a.second < b.second;
}
int main()
{
int n;
cin >> n;
vector<PII>v(n);
for (int i = 0; i < n; i++)
cin >> v[i].first >> v[i].second;
sort(v.begin(), v.end(), cmp);
int cnt = 0;
long long last = -1e9 - 5;
for (int i = 0; i < n; i++) {
if (last < v[i].first) {
last = v[i].second;
cnt++;
}
}
cout << cnt;
return 0;
}
题目链接3–区间分组
这题是要求对区间进行分组,任意两个区间有公共区间的不能分到一组,求分组的个数的最小值。
那么我们就按照区间左边从小到大排序,就像下面说的用教室问题,当然是开始时间越早,同样空间大小的利用率就越高。
我们用到的小根堆进行优化,小根堆存放的是每组最右边区间的右端点的,当对一个新的区间进行处理时,要开辟新的组只有两种情况,一是当前组个数位空,第二种是已经处理的区间的右端点的最小值都大于当前区间的左端点,因为当前区间的左端点小于右端点的最小值,那么所有组最右边区间的右端点都大于当前区间的左端点,且区间是按照左端点排序的,那么当前区间与所有组都会有交集。
为什么最后答案就是小根堆的大小呢?
因为如果heap里存在一组最右边的右端点在当前区间的左端点的左边,那么heap里右端点的最小值一定小于当前区间的左端点,直接heap.pop();,这一组的最右边的右端点就会被更新成当前区间的右端点heap.push(v[i].second);(选右端点最小的进行处理可以使空间利用率更高),然后进行小根堆的调整,也就是只要当前区间是存放在已存在的组内,当前区间的右端点就会把该组存放在heap里的数据覆盖掉,而如果当前区间要另开组的话,就直接加入heap,所以最后heap的大小就是我们要的答案。
详细证明好像听懂了但还是不是特别理解,上面的概述只是帮助理解,用来证明并不行,不够严谨。
#include<iostream>
#include<algorithm>
#include<utility>
#include<vector>
#include<queue>
using namespace std;
const int N = 1e5 + 5;
typedef pair<int, int>PII;
vector<PII>v(N);
bool cmp(PII a, PII b) {
return a.first < b.first;
}
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; i++)
cin >> v[i].first >> v[i].second;
sort(v.begin(), v.begin()+n, cmp);//按左端点排序
priority_queue<int, vector<int>, greater<int>>heap;//小顶堆,队头小于队尾
for (int i = 0; i < n; i++) {
if (heap.empty() || v[i].first<=heap.top()) //开新的一组
heap.push(v[i].second);
else{
heap.pop();
heap.push(v[i].second);
//新区间存放在heap的第一组,那么就把当前区间的右端点覆盖第1组,然后调整小顶堆。
}
}
cout << heap.size();
return 0;
}
对上面两类问题总个结
 第一种说的是取最大区间个数问题,第二个问题是最小区间分组情况问题
第一种说的是取最大区间个数问题,第二个问题是最小区间分组情况问题
题目链接4–区间覆盖
区间覆盖就是取最少的区间个数覆盖整个现状区间:
思路:按左端点进行排序,排序过后的区间发现中间有空就说明无法覆盖,如果可以覆盖就选择包含起点的区间中右端点最大的区间,然后将起点更新为选中区间的右端点,代码实现的一些细节我放在注释里面了。
为什么要按左端点排序呢,因为我们要实现完全覆盖区间是通过判断区间的左端点是否在起点左边,这样才能判断出起点是否存在在区间内部,然后为什么取右端点最长的区间,因为对于几个区间,起点都包含在区间内的话,选右端点小的区间也可以用右端点大的区间代替,求的是所用区间个数的最小值,既然是可以替代的,不如取右端点大的,对于下一个区间的选择,可以在右端点小的区间选的下一个区间肯定也能在右端点大的区间选择,右端点大的区间选择下一个区间的左端点的范围更广,也就更可能减少区间的个数。
#include<iostream>
#include<utility>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 1e5 + 5;
typedef pair<int, int>PII;
vector<PII>v(N);
bool cmp(PII a, PII b)
{
return a.first < b.first;
}
int main()
{
int beg, end;
cin >> beg >> end;
int n;
cin >> n;
for (int i = 0; i < n; i++)
cin >> v[i].first >> v[i].second;
sort(v.begin(), v.begin() + n, cmp);
int res = 0;
bool success = false;
for (int i = 0; i < n;) {
int j = i, maxr=-1e9;
while (j < n && v[j].first <= beg) {
//这样对j一循环可以把开始不在线状区间的全部排除掉
//用双指针,j指向i的下一个区间,如果开始连续多个区间都不在线状区间范围内,但是j一直后移就会超时
/*for (int j = i + 1; j < n; j++) {
if (v[j].first > beg) break;
if (v[j].second > v[maxp].second)
maxp = j;
}*/
maxr = max(maxr, v[j].second);
j++;
}
beg = maxr;
res++;
if (v[j].first > beg) break;
if (beg >= end) {
success = true;
break;
}
i = j;//距离上一次的i到j-1都没用了,maxr取了其中右端点最大的
}
if (success) cout << res;
else cout << -1;
return 0;
}
哈夫曼树
这题和之前写过的修理牧场一样,都是哈夫曼树的模型,当时写修理牧场的时候还没学哈夫曼树,现在学过了再看合并果子也就知道怎么写了,简单解释一下贪心原理。
题目的意思是要将n堆果子合并成一堆,每次任意取两堆,造成的代价(人体力的消耗)取决于这任意两堆的重量。
假设有三堆a,b,c我们先把a,b合并,新产生堆的重量(a+b),再把新一堆和c合并变成(a+b+c),总代价是a+b+a+b+c,先合并的 代价叠加的就多,这种有叠加的就可以看成哈夫曼树,当先合并数越小那么总代价就越小。
我们要求最小两堆在最低层,可以是兄弟节点,是可以!
简单证明一下,设n个石子中的任意两堆a,b,a<b,按照哈夫曼树的放置a在ha,b在hb,(ha比hb深),f1(n)=…+haa+hbb,如果交换a,b位置,f2(n)=…hab+hba,f1(n)-f2(n)=ha(a-b)+hb(b-a)=(ha-hb)(a-b)<0
所以f1(n)<f2(n)
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
int main()
{
priority_queue<int, vector<int>, greater<int>>heap;
int k, n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> k;
heap.push(k);
}
int res = 0;
while (heap.size() > 1) {
int a = heap.top(); heap.pop();
int b = heap.top(); heap.pop();
res += a + b;//每一次合并,达达可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。
heap.push(a + b);
}
cout << res;
return 0;
}
排序不等式
这题很简单的,前面人的打水时间是算在后面人的等待时间内的,而我们求得是等待时间的总和,这和上面那题其实差不多,都是越到后面,数据的叠加越多,所以使排在前面的数据越小叠加的就越少(按时间大小从小到大排序),证明方式也一样。
如果按从小到达排序的顺序结果记为f1(n),f1(n)=∑(n-i-1)*ti (i=1~n)
取其中任意两个数据为tj,tk,tj<tk,,j < k;
f1(n)=(n-1)*t1+(n-2)*t2+…+(n-j-1)*tj+…+(n-k-1)*tk+…
如果交换tj,tk的位置得到的结果是f2(n)
f2(n)=(n-1)*t1+(n-2)*t2+…+(n-j-1)*tk+…+(n-k-1)*tj+…
f1(n)-f2(n)=(n-j-1)*tj±(n-k-1)tk-(n-j-1)tk-(n-k-1)tj
=(n-j-1)(tj-tk)-(n-k-1)(tj-tk)
=(k-j)(tj-tk)<0
所以f1(n)<f2(n)
用反证法证明(我这个格式不是反证法,但大概意思是这样)
题目链接–排队打水
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5 + 5;
int t[N];
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; i++)
cin >> t[i];
sort(t, t + n);
long long res = 0;
for (int i = 0; i < n; i++)
res += (n - i - 1) * t[i];
cout << res;
return 0;
}
绝对值不等式
题目链接–货仓选址
这题代码非常简短,重点在于思路的诞生和证明:
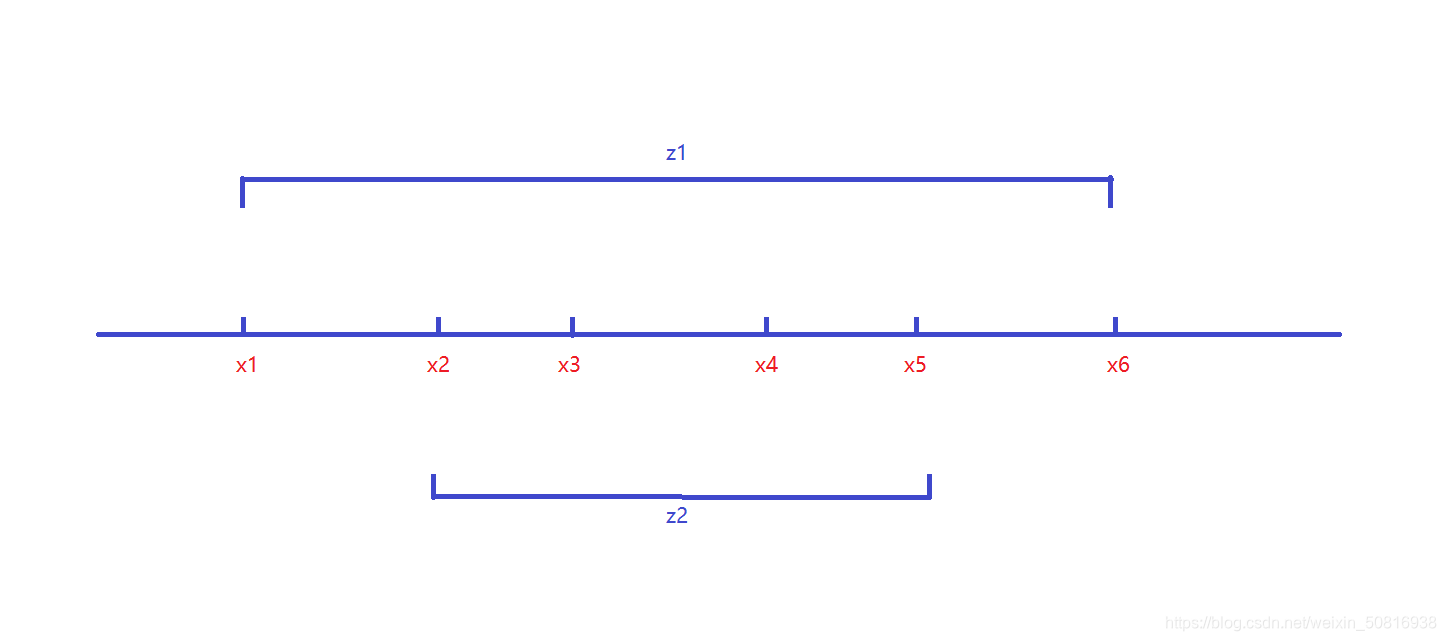
我们先将各点所在位置输入,然后按照在轴上面的位置从小到大排序,接着进行分组,将从开头数第i个位置点和从结尾数第i个位置点分为一组,如果点有偶数个正好两两分组,如果奇数个会剩余一个点,然后取中位数,也就是中点(偶数的话最中间一组两个点任意,奇数唯一确定),该点就是满足到各点距离和最小的一个解。
然后我们对此证明一下:
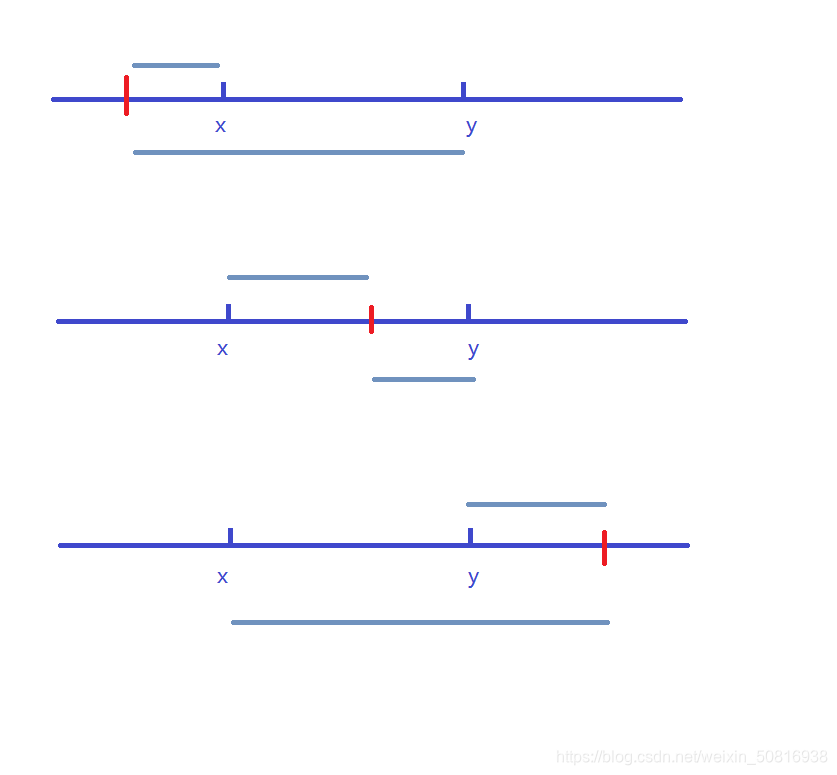
分别在一组点左边取点,中间取点,右边取点。
蓝灰色的部分是该点到一组点的距离和,可以看出当取点在最中间的时候,该点到一组点的距离和最小,设共有n个点,那么我们取点就取在第1个点和第n个点中间,第2个点和第n-1个点中间…最小的区间距离就是最中间的一组点,所以如果想要取点取在任意一组点的中间,只要把点控制在最中间一组点内就行(这就是为啥说偶数个点的时候取中点是其中一个解),然后因为点的个数不一定是偶数,也可能是奇数,当为奇数个点的时候分组会剩单独一个点,那么取的点到剩余这个点的最短距离为0,就是取在剩余这个点上,所以我们干脆直接取中点上就行。
res += abs(a[i] - a[n / 2]);
我们点的下标从0开始,这样n/2就是第0~第n-1点的中点下标。
n/2是向下取整,如果是偶数个n/2就是最中间一组点的右边那个点(n/2如果是下标从1开始就是最中间一组点的左边点,但因为是从0开始作下标,n=2k,n/2=k)。比如n=4,0~3,n/2=2。0,3一组,1,2一组。
如果是奇数n=2k+1,n/2=k,实际中间点是k+1(从1开始作为下标)但因为是从0开始作为下标,所以n/2=k就是奇数个点的中点。
#include<iostream>
#include<algorithm>
#include<math.h>
using namespace std;
const int N = 1e5 + 5;
int a[N];
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; i++)
cin >> a[i];
//最大可能超过int,开long long 吧,但试了int也没问题,可能测试数据没到那个范围吧
sort(a, a + n);
long long res = 0;
for (int i = 0; i < n; i++)
res += abs(a[i] - a[n / 2]);
cout << res;
return 0;
}
推公式
emmm这一块只能随缘了,平时写题多总结多积累
题目链接–耍杂技的牛
本题是将每个牛的重量和强壮值之和从小到大进行排序,这样排序后所有牛风险值的最大值是所有方案的最小值。
给个证明吧,为什么这么想我也不知道,可能靠经验吧。
如果要证明
ans==cnt(最优解=贪心方案的值)
也就是证明
ans<=cnt&&ans>=cnt
左边不等式最优解小于等于贪心方案求得的值:因为题目求的是最小值,所以最优解一定小于等于贪心方案求得的值。
接着证明右边式子,贪心方案数小于等于最优解。
哈?贪心方案数怎么会小于等于最优解,很奇怪吧,我的理解是这里的最优解并不是实际上的最优解,而指的是如果我们不采用贪心方案来计算所求得的假的最优解。
按照贪心方案wi+si<wi+1+si+1
如果不按照贪心方案,我们不妨就将第i个位置上的牛和第i+1个位置上的牛进行交换,这样就不满足牛是从小到大递增的。
交换前:
第i个位置上的牛的风险值是w1+w2+…+wi-1-si
第i+1个位置上的牛的风险值是w1+w2+…+wi-1+wi-si+1
交换后:
第i个位置上的牛的风险值是w1+w2+…+wi-1-si+1
第i+1个位置上的牛的风险值是w1+w2+…+wi-1+wi+1-si

我们把四个式子相同的部分去掉
交换前:
第i个位置上的牛的风险值是-si
第i+1个位置上的牛的风险值是wi-si+1
交换后:
第i个位置上的牛的风险值是-si+1
第i+1个位置上的牛的风险值是wi+1-si
再给每个式子加上si+1+si
交换前:
第i个位置上的牛的风险值是si+1
第i+1个位置上的牛的风险值是wi+si
交换后:
第i个位置上的牛的风险值是si
第i+1个位置上的牛的风险值是wi+1+si+1

wi+si<wi+1+si+1
si+1可能比wi+si要大,所以交换前所有牛的最大值如果不是第i只或者第i+1只,那么交换前后一样,cnt=ans,如果是第i只或者第i+1只,交换前所有牛的最大值要么si+1要么wi+si
交换后所有牛的最大值是wi+1+si+1
wi+1+si+1>wi+si
wi+1+si+1>si+1
不按照贪心方案求得最优解永远大于等于用贪心方案求得的最优解
ans>=cnt得证
所以贪心求得最大值就是最优解(最大值中的最小值)
芜湖~我好像有点悟了y总这种方法的证明了,区间那边四道题都可以用ans<=cnt&&ans>=cnt证明,这样证明比文字理解型叙述严谨多了。
果然我接受思想很慢,但是放着放着莫名其妙就悟了,开心呢!!
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 50005;
typedef long long ll;
struct cattle {
ll w, s;
}C[N];
bool cmp(struct cattle a, struct cattle b)
{
return a.w + a.s < b.w + b.s;//从小到大排序
}
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; i++)
cin >> C[i].w >> C[i].s;
sort(C, C + n, cmp);
ll sum=0, Max=-0x3f3f3f3f;
for (int i = 0; i < n; i++) {
Max = max(Max, sum - C[i].s);
sum += C[i].w;
}
//排序使得最大风险值最小,求的是这个最大风险值的最小值
cout << Max;
return 0;
}
截至到8.25号1.29,算法基础课全部完成(虽然有些已经忘掉了,但毕竟学过,复习起来应该比较快)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号