面向递归编程
当我们开始学习一门语言的时候,第一步都会写一个hello world程序开始。同理,当我们对编程有点领悟的时候,我觉得是从理解递归开始的。倒不是说不会递归就完成不了需求,写不好代码。俗话说存在就是合理,事实上编程中的很多概念和思想都是围绕递归展开的,这就导致我们必须去面对它,另外理解和运用好递归确实能让我们的编程水平有一个质的飞跃。
循环与递归的对比
编写程序的时候经常需要操作列表,以下代码的主要工作是将整数列表中的各个元素进行打印输出,代码虽然简单但却是很多复杂软件的组成部分,很多CURD BOY天天都是写这个代码操作数据的。
public void loopPrint(List<Integer> list) {
for(int i = 0 ; i < list.size(); i++) {
System.out.print(list.get(i) + " ");
}
}
代码清单1-1 循环
上面的代码能正常工作没有问题,但我们作为一个有追求的程序员,我们与众不同使用递归算法进行改写完成列表打印,代码如下: public void recursionPrint(List<Integer> list, int index) {
if(index == list.size()) return;
System.out.print(list.get(index) + " ");
recursionPrint(list, index + 1);
}
代码清单1-2 递归
接着编写测试测试类对上面两个函数进行测试,结果如下:public class RecursionTest {
public static void main(String[] args) {
List<Integer> list = Arrays.asList(1, 2, 3, 4);
RecursionTest recursionTest = new RecursionTest();
//loop
recursionTest.loopPrint(list);
System.out.println("--------");
//recursion
recursionTest.recursionPrint(list, 0);
}
}
==运行结果==
1 2 3 4
--------
1 2 3 4
代码清单1-3 测试打印列表
可以看出以上两段程序只是写法不同,完成的操作是一样的。循环比较符合人的直觉,而递归看起来比较简洁。有些人会觉得递归很难理解,是因为把关注点到方法如何调用它自己上,用头脑不停模拟程序压栈,这样其实是不对的。坦白讲,只需要关注在哪里开始哪里结束就好了,以及递归方法做了什么,这样理解起来省时省力。生活中递归
生活中有些场景也能看到递归,递归的前半段是先一路走到底,后半段是再原路返回的过程。现在假设你坐在电影院的座位上,朋友迟到问你在第几排,可是你的电影票丢了,这时候你该怎么办?我猜你就会问前排的人他在第几排,那如果前排的人也不清楚呢?这时候他也继续往前问直到到第一排,当传到第1排时,因为前面没有人就回说在第1排,后排的人一听就知道自己在第2排,然后依次往后报数,最后传到你这边,只需要将听到的排数加1就得到你的排数啦,然后你就回复给你的朋友_。现实中很难遇到一直往前问的情况,这里只是为了更好地说明。整个过程如图2-1所示,图中起点和终点都是A,序号1到序号4对应递归的前半段(递),序号5到序号8对应递归的后半段(归)。
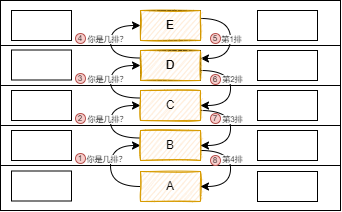
图2-1 电影院问第几排
在开发移动应用也常遇到递归,APP为了获取更多的新用户,一般都会有奖励邀请人的机制,成功邀请用户注册后邀请人就会得到相应的奖励。有些应用甚至会奖励邀请人的邀请人,总之就是找到邀请人并给他们发奖励。假如公司要求你写一个奖励模块,你会怎么写呢?以下是一种实现地思路:
class User {
private Integer userId;//用户的id
private User inviteUser;//邀请用户
public User(Integer userId, User inviteUser) {
this.userId = userId;
this.inviteUser = inviteUser;
}
//getter setter...
}
代码清单2-2 用户实体
//获取注册用户的所有邀请人
public void findInviteUsers(User user, List<Integer> res) {
// 当查找到用户没有上级用户时,说明已经没有上级(邀请人)
User inviteUser = user.getInviteUser();
if (inviteUser == null) return;
res.add(inviteUser.getUserId());
findInviteUsers(inviteUser, res);
}
代码清单2-3 查找上级邀请人
public static void main(String[] args) {
// u3邀请u2,u2邀请u1
User u3 = new User(20, null);
User u2 = new User(10, u3);
User u1 = new User(1, u2);
//获取u1所有上级邀请人
List<Integer> res = new ArrayList<>();
new InviteUserTest().findInviteUsers(u1, res);
System.out.print("u1所有邀请人的ID列表:");
if (res.size() == 0) return;
for (int i = 0; i < res.size() - 1; i++) {
System.out.print(res.get(i) + ", ");
}
System.out.print(res.get(res.size() - 1));
}
代码清单2-4 打印用户上级邀请人
可见递归思想普遍存在现实生活中,只要善于发现,很多问题都能抽象为递归并加以解决。
数据结构与算法中的递归
树的遍历
一般来讲我们学习数据结构和算法的时候都是从最基础的数据结构开始学起的,它们的顺序大概是数组、链表、栈,队列,二分查找,树,回溯,贪心和动态规划。从树这个数据结构后递归算法就一直被使用。如果不能很好理解递归,就会觉得阅读代码难度很高,反过来如果理解了递归则会觉得它们都在同样的框架下编码,反而见惯不惯。举个例子,我们知道树的遍历大致分为前序、中序和后序,那以下的树的输出结果是什么呢?
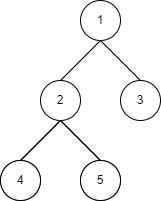
图3-1 二叉树
答案是1 2 4 5 3,不知道你有没有答对。我们通常所说的前序、中序后序,其实指的是中间节点被遍历时的位置,前序的顺序是中左右、中序是左中右、后续是左右中。所以上图中的遍历顺序如下箭头所示:
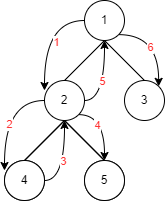
图3-2 二叉树遍历
以下是二叉树前序遍历的代码。
class TreeNode {
TreeNode left;
TreeNode right;
int val;
}
代码清单3-3 树节点实体
public class TreeTest {
//前序遍历
public void preTravel(TreeNode root) {
if (root == null) return;
System.out.print(root.val + " ");
preTravel(root.left);
preTravel(root.right);
}
public static void main(String[] args) {
TreeNode p = new TreeNode(1);
TreeNode l2 = new TreeNode(2);
TreeNode r3 = new TreeNode(3);
TreeNode l4 = new TreeNode(4);
TreeNode r5 = new TreeNode(5);
p.left = l2;
p.right = r3;
l2.left = l4;
l2.right = r5;
//传入根节点,前序遍历二叉树
new TreeTest().preTravel(p);
}
}
==运行结果==
----前序遍历-----
1 2 4 5 3
----广度优先遍历-----
1 2 3 4 5
代码清单3-4 前序遍历二叉树
可见树的遍历和递归息息相关,理解递归也就能更好地理解二叉树。递归在树形结构遍历时,一般会遍历到树的子节点后才返回,这就是所谓的深度优先遍历(DFS)。二叉树遍历使用递归外,多叉树的遍历也同样使用递归,比如下面的回溯算法。
回溯算法
回溯的本质就是穷举,穷举的过程相当于多叉树的遍历。与二叉树的遍历不同,二叉树中的子节点最多有2个(左节点、右节点),而回溯算法的子节点可以超过2个甚至更多,实际数量依据问题而定。回溯遍历是二叉树遍历的通用版本,二叉树遍历是回溯遍历的子集。由于二叉树遍历与递归息息相关,那回溯自然也是。一般回溯算法适合解决组合、排列、路径等问题,以下是回溯算法的模板:
void backtracking(参数) {
if(终止条件) {
//存放结果
return;
}
for(选择 : 该层可以选择的列表) {
//选择操作
backtracking(参数);
//撤销操作
}
}
代码清单4-1 回溯算法模板
力扣题77,给出数值为1到n的n个数,返回k个数的组合。
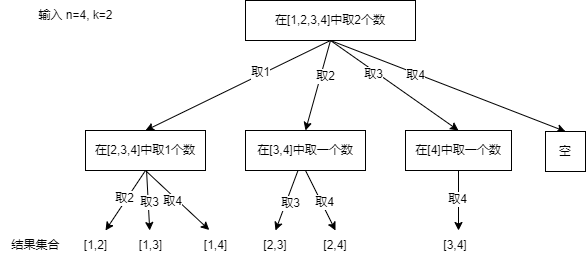
图4-2 K个数组合
以下是k个数组合的代码实现:
List<List<Integer>> res = new ArrayList();
List<Integer> path = new LinkedList();
void backtracking(int n, int k, int startIndex) {
if(path.size() == k) {
res.add(new ArrayList<>(path));
return;
}
// 选择 : 该层可以选择的列表
for(int i = startIndex ; i <= n; i++) {
path.add(i);//增加元素到路径
backtracking(n, k, i + 1);
path.removeLast();//在路径中撤销元素
}
}
代码清单4-3 获取k个数组合列表
为了避免程序走进不要的分支计算,可以对程序做剪支的操作:
List<List<Integer>> res = new ArrayList();
List<Integer> path = new LinkedList();
void backtracking(int n, int k, int startIndex) {
if(path.size() == k) {
res.add(new ArrayList<>(path));
return;
}
// 选择 : 该层可以选择的列表
// n - (k - path.size()) + 1 表示从这个位置开始取值才有意义
//比如在1、2、3、4、5 中获取 k=2,则 5 - (2 - 1) + 1 = 4; 说明当组合已有一个数的情况下
//从位置4开始才有意义。
for(int i = startIndex ; i <= n - (k - path.size()) + 1; i++) {
path.add(i);//增加元素到路径
backtracking(n, k, i + 1);
path.removeLast();//在路径中撤销元素
}
}
代码清单4-4 获取k个数组合列表(剪支)
回溯就通过设置状态和撤销状态在多叉树中遍历的,当满足条件时将结果收集起来然后回退。但是在遍历的过程的如果发现节点之前已经被计算过了,那么我们还有必要重复计算吗?要想回答这个问题,就要讲到下面的动态规划了。
动态规划
记得刚开始听到动态规划这个名字的时候,觉得这是一种高大上的算法。后来慢慢接触发现动态规划其实是一种降低时间复杂度的算法。由于递归是自顶向下的遍历的,那么在层层递归的过程中难免就会遇到一些重复的子问题。一般而言,当遇到相同子问题时直接使用计算过的结果即可,这样我们就可以免除多余的计算。有了这个想法,就可以构造一个字典,在遍历的过程中将每个节点的计算好的值记录起来,当遍历到的节点在字典中能找到就直接获取,这就是动态规划。除了构造字典,我们还可以使用迭代的方法,找到最底层的值开始自底向上推,这与递归自顶向下的方向相反,但本质是一样的。下面是斐波那契数列的递归代码,求第n个数的值。
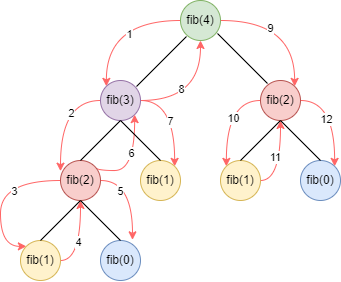
图5-1 斐波那契数列运行路径
int fib(int n) {
if(n == 0 || n == 1) return n;
// 递归表达式
return fib(n -1) + fib(n -2);
}
代码清单5-2 斐波那契数列递归
代码清单5-2的时间复杂度为O(2 ^n),空间复杂度是顶点到节点的深度O(n)。我们知道时间复杂度从小到大的排列顺序是O(1) < O(log(n) < O(n) < O(n log(n)) < O(n^n) < O(n!),可以看出n的n次方是一个非常耗时的算法,而导致时间复杂度高的原因是因为重复计算了相同的节点,所以需要进一步的优化。上面说过我们可以构造一个字典,也就是使用备忘录进行优化,这样就不会有重复计算的问题,进而将时间复杂度从O(n^2)降为O(n)
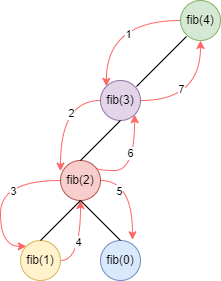
图5-3 斐波那契数列运行路径(备忘录)
Map<Integer, Integer> memo = new HashMap<>();
int fib(int n, Map<Integer, Integer> memo) {
if(n == 0 || n == 1) return n;
if(memo.containsKey(n)) return memo.get(n);
//
int tmp = fib(n -1, memo) + fib(n -2, memo);
memo.put(n, tmp);
return tmp;
}
代码清单5-4 斐波那契数列运行路径(备忘录)
上面函数fib中的memo是一个字典(备忘录),当遇到相同值时,从字典中获取值,所以相同的节点只需要计算一次。除了使用备忘录,我们可以从最小的值开始迭代,自底向上求出fib(n)的值
int fib(int n) {
int p = 0, c = 1;
for(int i = 2; i <= n; i++) {
int sum = p + c;
p = c;
c = sum;
}
return c;
}
代码清单5-5 斐波那契数列自底向上递推
从上面的各种例子可以看出递归是普遍存在的,开发中遇到的问题远不止如此,这也只是冰山一角。但是我们掌握理解递归算法,能让我们更好地看清复杂算法背后的本质,提升自我认知和编程水平。 文章中的代码可以从这里下载测试。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号