Sqrt(x) LeetCode
Question:
https://oj.leetcode.com/problems/sqrtx/
解答:
1)二分法。
取中点,如果当前点平方大于x,前半段继续二分。否则后半段继续二分。需要注意的是求的值是平方最接近但是小于,或者等于x。所以中点如果小于x,后半段需要包括这个中点。这就需要中点能够大于开始的点。其次还有一点需要注意的是平方可能超过int的最大值,简单的做法就是用long long来保存这个平方。
int sqrt2(int x) { if (x <= 0) return 0; if (x == 1) return 1; int s = 1; int e = x/2; while (1) { if (s == e) return s; // make sure middle is always > s int middle = (s+e)/2+1; long long m2 = (long long)middle*(long long)middle; if (m2 == x) { return middle; } else if (m2 > x) { e = middle-1; } else { s = middle; } } return 0; }
2)牛顿迭代法
这是数学上的求近似值的办法。
From Wiki:
In numerical analysis, Newton's method (also known as the Newton–Raphson method), named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots (or zeroes) of a real-valued function.
The Newton–Raphson method in one variable is implemented as follows:
Given a function ƒ defined over the reals x, and its derivative ƒ', we begin with a first guess x0 for a root of the function f. Provided the function satisfies all the assumptions made in the derivation of the formula, a better approximation x1 is
Geometrically, (x1, 0) is the intersection with the x-axis of the tangent to the graph of f at (x0, f (x0)).
The process is repeated as
until a sufficiently accurate value is reached.
对于函数f(x)=0,和任意一个起点xi,持续一下的步骤直到xi和xi+1足够相同。
xi+1=xi-f(x)/f'(x).
对于我们这个问题,f(x) = x2-n,所以f'(x) = 2x.
xi+1=xi-f(x)/f'(x) = xi-(xi2-n)/(2xi) = (xi+n/xi)/2
因为最终的近似结果平方可能大于x也可能小于x(不太确定,因为最终结果是double取整,本身已经小于value),所以保险起见需要最后判断需要不需要减一。
int sqrt(int x) { const double dmin = 0.000001; double value = 1; double last = 0; while (abs(value - last) > dmin) { last = value; value = (value + x/value) / 2; } int n = (int)value; if (n*n > x) n = n-1; return n; }


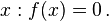
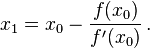
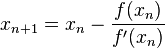

 浙公网安备 33010602011771号
浙公网安备 33010602011771号