狼蛛 - Tarantula - Dijkstra
狼蛛
时限:最多 40 个用例,1.5 秒 (C/C++),2 秒 (Java)
当前有一个N行M列大小的二维网格型迷宫。假设左上角格子的坐标是[1, 1],右下角格子的坐标是[N, M]。你目前在 [1, 1] 格子上。在 [N, M] 格子有个出口,可以逃出网格迷宫。在网格内只能以上下左右四个方向移动。
这个网格迷宫中有狼蛛,如果被狼蛛咬到,那么肢体会无力或丧失意识,导致逃出网格迷宫会很困难。幸运的是,狼蛛数量并不多,所以在每个格子中碰不到狼蛛的可能性很高,概率在99.99% 到 100% 之间。
如图1所示,假设有一个迷宫,每个格子给出了碰不到狼蛛的概率。
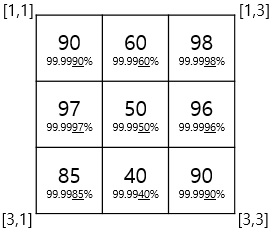
(图 1)
这时,碰不到狼蛛的概率(%)的小数点后第三位开始的值将定义为 P,P 为介于 0 到 100 之间的整数,这也是跟每个格子中写的大数字相关。(100 表示 100% 的概率。)
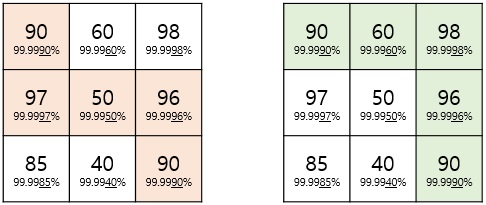
(图 2)
如果按照图2左边所示的橙色路线移动时,碰不到狼蛛而逃出迷宫的概率为 99.9990% * 99.9997% * 99.9950% * 99.9996% * 99.9990% = 99.9923%。如果按照右边所示的绿色路线移动时,碰不到狼蛛而安全逃出迷宫的概率为 99.9990% * 99.9960% * 99.9998% * 99.9996% * 99.9990% = 99.9934%,而这是没有碰到狼蛛而最安全的逃出迷宫的概率
当每个格子中给出碰不到狼蛛的概率时,从[1, 1]位置出发到达[N, M]位置后,请求出通过出口逃出迷宫为止,不碰到狼蛛可以最安全的逃出迷宫的概率。
[限制条件]
- 二维网格的行数 N 和列数 M 是介于 1 到 300 之间的整数。
- P是碰不到狼蛛的概率的小数点后第三位开始的数值,是介于 0 到 100 之间的整数。
(0表示碰不到狼蛛的概率为 99.9900%,1表示碰不到狼蛛的概率为 99.9901%,… 100 表示概率为 100%。) - 在[1, 1] 和 [N, M]位置上也可能会碰到狼蛛。
[输入]
首先给出测试用例数量T,然后给出T种测试用例。每个测试用例的第一行空格区分给出二维网格的大小N,M。接下来通过N行,每行空格区分给出M个从各位置移动到另一个格子时碰不到狼蛛的概率(P)值。
[输出]
一个测试用例输出一行。每个测试用例都输出“#x”(其中x表示测试用例编号,从 1 开始),然后输出不碰到狼蛛逃出迷宫的最高概率(精确到小数点后6位,在第7位数四舍五入)。例如,答案为 0.9999002的情况,输出为 0.999900,不省略0。
[输入输出 案例]
(输入)
2
3 3
90 60 98
97 50 96
85 40 90
6 4
10 50 30 20
90 99 77 88
27 50 33 99
5 73 99 99
4 21 98 40
9 59 99 100
(输出)
#1 0.999934
#2 0.999858
思路: Dijkstra
package pro.dijkstra;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
/**
* Dijkstra
* @author XA-GDD
*
*/
public class Tarantula_0315 {
static int T,N,M;
static TarantulaNode [][] prob = new TarantulaNode [302][302];
static int [][] dire = new int [][] {{-1,0},{0,1},{1,0},{0,-1}}; //移动方向
static double num = 1000000;
static double ANS;
public static void main(String[] args) throws IOException {
System.setIn(new FileInputStream("D:\\workspace\\sw_pro\\test_case\\sample_input_0315.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
T = Integer.parseInt(st.nextToken());
for(int testCase=1;testCase<=T;testCase++) {
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
for(int i=1;i<=N;i++) {
st = new StringTokenizer(br.readLine());
for(int j=1;j<=M;j++) {
int val = Integer.parseInt(st.nextToken());
//此处一直要相除,勿直接拼接
double probVal = 0.9999+(double)val/num;
prob[i][j] = new TarantulaNode(i,j,probVal);
}
}
ANS = dijkstra(prob[1][1]);
System.out.printf("#%d %.6f\n",testCase,ANS);
}
}
static double dijkstra(TarantulaNode start) {
PriorityQueue<TarantulaNode> pq = new PriorityQueue<TarantulaNode>(new Comparator<TarantulaNode>() {
@Override
public int compare(TarantulaNode o1, TarantulaNode o2) {
if(o2.maxProb>o1.maxProb) {
return 1;
}else {
return -1;
}
}
});
start.maxProb = start.prob;
pq.add(start);
TarantulaNode curr;
TarantulaNode next;
while(!pq.isEmpty()) {
curr = pq.poll();
if(curr.visited==1) {
continue;
}
curr.visited=1;
for(int i=0;i<4;i++) {
int x = curr.x + dire[i][0];
int y = curr.y + dire[i][1];
if(!isValid(x,y)) {
continue;
}
next = prob[x][y];
if(next.maxProb < curr.maxProb*next.prob) {
next.maxProb=curr.maxProb*next.prob;
pq.add(next);
}
}
}
return prob[N][M].maxProb;
}
static boolean isValid(int x, int y) {
return x>0 && x<=N && y>0 && y<=M;
}
}
class TarantulaNode{
int x;
int y;
int visited;
double prob;
double maxProb;
TarantulaNode(int x,int y, double prob){
this.x = x;
this.y = y;
this.prob = prob;
this.visited = 0;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号