P8681 [蓝桥杯 2019 省 AB] 完全二叉树的权值

题目描述

给定一棵包含N 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是​，如下图所示：

 

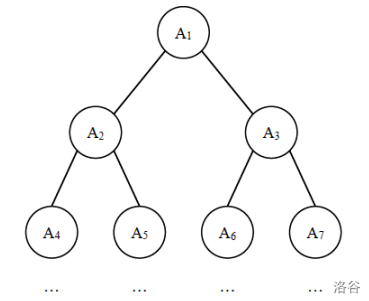
现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点权值之和最大？如果有多个深度的权值和同为最大，请你输出其中最小的深度。

注：根的深度是 1。

输入格式

第一行包含一个整数 N。

第二行包含N 个整数 ​。

输出格式

输出一个整数代表答案。

输入输出样例

输入 #1复制

7

1 6 5 4 3 2 1

输出 #1复制

2

说明/提示

对于所有评测用例，1<=N<=10⁵ ,-10⁵<=a_i <=10⁵。

蓝桥杯 2019 省赛 A 组 F 题（B 组 G 题）。

题意分析

由完全二叉树的数组存储可知，第一层的元素个数为1个元素，第二层的元素个数为2，第i层的元素为2ⁱ  个，故问题转化为分别统计各层元素的和，同时比较其最大值在第几层，如果最大值相同求层数最小的哪个层数是多少。

代码一

#include<iostream>
#include<cmath>
using namespace std;
int main()
{
         long long ans=-10e10,cur=0;//是到当前位置时的最大值为ans，cur为当前层所有元素之和，注意cur，ans的取值范围。
         int n,b,c=1,sd=1,l=2;//sd为最大值所在的层数，l表示当前是第几层
         b=c=2;//当c计算第i层有几个元素，b表示当前层已统计了几个元素。
         cin>>n;
         cin>>ans;
         for (int i=2;i<=n;i++)
         {
                  int x;
                  cin>>x;
                  cur+=x;
                  b--;
                  if (b==0||i==n)
                  {
                          if (ans<cur)
                          {
                                   ans=cur;
                                   sd=l;        
                          }
                          l++;
                          c*=2;
                          b=c;
                          cur=0;
                  }
         }
         cout<<sd<<endl;
}

　

代码二，树的遍历法

#include<iostream>
using namespace std;
const int maxn=1e5+10;
int a[maxn],n,dep;
long long b[100];
void dfs(int x,int d)//x当前结点编号,d当前结点的深度。
{
         if (x>n) return ;
         dep=max(dep,d);//树的深度
         b[d]+=a[x];//同一层的元素的和
         dfs(2*x,d+1);
         dfs(2*x+1,d+1);
}
int main()
{
         cin>>n;
         for (int i=1;i<=n;i++)
         {
                  cin>>a[i];
         }
         dfs(1,1);
         int ansi=1;
         for (int i=1;i<=dep;i++)//查找第一个最大值的位置，思考与dfs是否可以合并
         {
                  if (b[ansi]<b[i]) ansi=i;
         }
         cout<<ansi<<endl;
}

　　合并一下

#include<iostream>
using namespace std;
const int maxn=1e5+10;
int a[maxn],n,ansi=1;
long long b[100];
void dfs(int x,int d)
{
      if (x>n) return ;
      b[d]+=a[x];
      dfs(2*x,d+1);
      dfs(2*x+1,d+1);
      if (b[ansi]<b[d]) ansi=d;
}
int main()
{
      cin>>n;
      for (int i=1;i<=n;i++)
      {
             cin>>a[i];
      }
      dfs(1,1);
      cout<<ansi<<endl;
}