堆排序
堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。
堆
堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图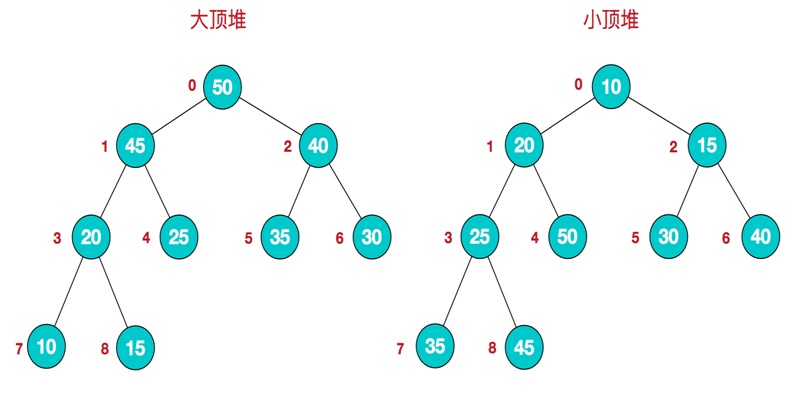
同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子
该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是：
大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] ?
小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2] ?
ok，了解了这些定义。接下来，我们来看看堆排序的基本思想及基本步骤：
另一个表示方法是从下标1开始
堆排序基本思想及步骤
堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了
想一想这个结果是什么排序？
步骤一 构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。
a.假设给定无序序列结构如下
arr: 4 6 8 5 9
2.此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。
再简单总结下堆排序的基本思路：
a.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换，将最大元素“沉”到数组末端;
c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。
#include<iostream>
using namespace std;
const int Maxn=100010;
struct Heap
{
int len;
int a[Maxn];
int left(int x)
{
return 2*x+1;
}
int right(int x)
{
return 2*x+2;
}
int fa(int x)
{
return (x-1)/2;
}
int top()
{
if (len>0)
return a[0];
}
void sift_up(int x)
{
while(x)
{
int pre=fa(x);
if (a[pre]<a[x])
{
swap(a[pre],a[x]);
}
else
{
break;
}
x=pre;
}
return ;
}
void insert(int val)
{
a[++len]=val;
sift_up(len);
}
void sift_down(int x)
{
while (x<len)
{
int l=left(x);
int r=right(x);
int t=x;
if (l<len)
{
if (a[l]>a[t])
{
t=l;
}
}
if (r<len)
{
if (a[r]>a[t])
{
t=r;
}
}
if (t!=x)
{
swap(a[t],a[x]);
x=t;
}
else
{
break;
}
}
}
void pop()
{
swap(a[0],a[len-1]);
len--;
sift_down(0);
}
void sort()
{
build_heap();
int l=len;
for (int i=0;i<l;i++)
pop();
}
void build_heap()
{
for (int i=len/2-1;i>=0;i--)
{
sift_down(i);
}
}
};
Heap h;
int main()
{
int n;
cin>>n;
h.len=n;
for (int i=0;i<n;i++)
{
cin>>h.a[i];
}
h.build_heap();
cout<<h.top()<<endl;
int x;
cin>>x;
h.insert(x);
cout<<h.top()<<endl;
cin>>x;
h.insert(x);
cout<<h.top()<<endl;
}
/*
5
1 8 3 4 5
6
9
out
8
8
9
*/
优先队列
#include<iostream>
using namespace std;
const int Maxn=100010;
struct Heap
{
int len;
int a[Maxn];
int left(int x)
{
return 2*x+1;
}
int right(int x)
{
return 2*x+2;
}
int fa(int x)
{
return (x-1)/2;
}
int top()
{
if (len>0)
return a[0];
}
void sift_up(int x)
{
while(x)
{
int pre=fa(x);
if (a[pre]<a[x])
{
swap(a[pre],a[x]);
}
else
{
break;
}
x=pre;
}
return ;
}
void insert(int val)
{
a[++len]=val;
sift_up(len);
}
void sift_down(int x)
{
while (x<len)
{
int l=left(x);
int r=right(x);
int t=x;
if (l<len)
{
if (a[l]>a[t])
{
t=l;
}
}
if (r<len)
{
if (a[r]>a[t])
{
t=r;
}
}
if (t!=x)
{
swap(a[t],a[x]);
x=t;
}
else
{
break;
}
}
}
void pop()
{
swap(a[0],a[len-1]);
len--;
sift_down(0);
}
void sort()
{
build_heap();
int l=len;
for (int i=0;i<l;i++)
pop();
}
void build_heap()
{
for (int i=len/2-1;i>=0;i--)
{
sift_down(i);
}
}
};
Heap h;
int main()
{
int n;
cin>>n;
h.len=n;
for (int i=0;i<n;i++)
{
cin>>h.a[i];
}
h.build_heap();
cout<<h.top()<<endl;
int x;
cin>>x;
h.insert(x);
cout<<h.top()<<endl;
cin>>x;
h.insert(x);
cout<<h.top()<<endl;
}
/*
5
1 8 3 4 5
6
9
out
8
8
9
*/
