蓝桥真题
有奖问答
这种选择导致分支可以使用递归
我个人觉得洛谷的答案错了,如果按能得到洛谷答案的代码,改成求30题对30道,最多对30道的话,得到的是0,应该把限制条件改为能计算答对10道题的方案,因为最多十道题不是不能达到10道题
DFS
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
int ans=0;
void work(int t,int m)//已答完的题和已经拿到的分数
{
if(m==7&&t==30) ans++;//求的是结束后的积分,所以==30,中途结束的可认为是自那之后一直没答对
if(t==31) return;
if(m==11) return;
work(t+1,m+1);
work(t+1,0);
}
int main() {
work(0,0);
cout<<ans;
return 0;
}
DP
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
int dp[40][40];
int main() {
dp[0][0]=1;
for(int i=1;i<=30;i++)
{
for(int j=0;j<=10;j++)
{
if(j<=9) dp[i][j+1]+=dp[i-1][j];
dp[i][0]+=dp[i-1][j];
}
}
cout<<dp[30][7];
return 0;
}
| -------------------------------------------------------------------------------------------------- |
平方差
推柿子,得到 x=(y−z)×(y+z),可知 x 满足可以拆成 2 个奇偶性相同的数的乘积。
如果是奇数,直接拆成 1 和它本身即可。
如果是偶数,因为要拆成 2 个偶数,所以应是 4 的倍数,此时一种拆分为拆成 2 和 x 除以 2。
至此,答案为 l 到 r 中 奇数 和 4 的倍数 的个数。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int f(int x) {//小于等于x的奇数个数
if (!x) return 0;
return (x + 1) / 2;
}
int g(int x) {//小于等于x的4的倍数个数
return x / 4;
}
int main() {
int l, r; cin >> l >> r;
cout << f(r) - f(l - 1) + g(r) - g(l - 1);
return 0;
}
| -------------------------------------------------------------------------------------------------- |
更小的数
难得一遍过
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
string s;
LL ans;
int main() {
cin>>s;
for(int i=0;i<s.length()-1;i++)
{
for(int j=i+1;j<=s.length()-1;j++)
{
for(int k=1;k<=(j-i+1)/2;k++)
{
if(s[i+k-1]-'0'>s[j-k+1]-'0')
{
ans++;
break;//i-j区间已经查完,更小的子区间以后会查到,要break防止重复
/*cout<<s[i+k-1]<<" "<<s[j-k+1]<<" "<<i<<" "<<j<<endl;*/
}
else if(s[i+k-1]-'0'<s[j-k+1]-'0') break;
}
}
}
cout<<ans;
return 0;
}
| -------------------------------------------------------------------------------------------------- |
做了一天,感觉自己真不是搞算法的料
一开始把题目看错了,看成了不同的落子顺序也算不同的结局,一顿饭吃完还没跑完答案
其实是不算顺序,只看最终棋局
题目是DFS
每次下一个子,可以是 1 或者是 2 ,maps【i】【j】= 1 或者 2 .
先看下 1 的情况 ,maps【i】【j】= 1 , 然后另一个玩家落子 ,dfs ( i , j + 1 )
然后是 2 的情况 ,maps【i】【j】= 2 , 然后另一个玩家落子 ,dfs ( i , j + 1 ).
下到最后肯定会填满,满了之后检查 (check) 棋局是否满足要求,即没有 横 竖 斜 的 五子连珠
满足的话就 ans++;
之后return , 考虑 上一步棋的另一种情况
如果这步棋 1 , 2 都考虑了,那就这步棋撤回,maps【i】【j】= 0,
然后return ,考虑 上一步棋的另一种情况
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
LL ans,maps[6][6];
bool check()
{
int c1=0,c2=0;
for(int i=1;i<=5;i++)
{
for(int j=1;j<=5;j++)
{
if(maps[i][j]==1) c1++;
if(maps[i][j]==2) c2++;
}
}
if(c1-c2!=1) return true; //要符合条件的话,先手的13棋,后手12棋,先手-后手=1
for(int i=1;i<=5;i++)
{
bool t=true;//要注意检查每行是否有连珠,不能放外面初始化,不然一行没有连珠的话,下面可能连珠的当成没有连珠了,下面同理,因为这个卡了好久
for(int j=1;j<=5;j++)
{
if(maps[j][i]!=maps[1][i]) t=false;
}
if(t) return true;
}
for(int i=1;i<=5;i++)
{
bool t=true;
for(int j=1;j<=5;j++)
{
if(maps[i][j]!=maps[i][1]) t=false;
}
if(t) return true;
}
bool t=true;
for(int k=1;k<=5;k++)
{
if(maps[k][6-k]!=maps[1][5]) t=false;
}
if(t) return true;
t=true;
for(int k=1;k<=5;k++)
{
if(maps[k][k]!=maps[1][1]) t=false;
}
if(t) return true;
return false;
}
void dfs(int i,int j)
{
if(j>=6)
{
i++,j=1;
}
if(i>=6)
{
if(!check()) ans++;
return;
}
maps[i][j]=1;
dfs(i,j+1);
maps[i][j]=2;
dfs(i,j+1);
maps[i][j]=0;
return;
}
int main() {
dfs(1,1);
cout<<ans;
return 0;
}
| -------------------------------------------------------------------------------------------------- |
训练士兵
挺简单的一道题,每次检查所有士兵的训练费用是否小于组团训练费用,小的话就全体单独训练,大于就组团训练
我的方法是每次用 当前最小的次数 - 已经训练的次数 ,但之前一直错误地把 已经训练的次数 当成 每次训练的次数的累加 了
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
LL n,S,ans,ttc,ttt;
struct P{
LL cost=0,time=0;
P()=default;
P(LL c,LL t):cost(c),time(t){};
bool operator<(const P & b)const{
return time>b.time;
}
};
priority_queue<P> p;
int main() {
cin>>n>>S;
for(int i=1;i<=n;i++)
{
LL a,b;
cin>>a>>b;
ttc+=a;
p.push(P(a,b));
}
while(!p.empty())
{
LL mc=0,mt=p.top().time;
if(ttc<=S)
{
ans+=ttc*(mt-ttt);
}
else
{
ans+=S*(mt-ttt);
}
while(!p.empty()&&p.top().time==mt)
{
mc+=p.top().cost;
p.pop();
}
ttc-=mc;
ttt=mt;//害人精,找了我一天
}
cout<<ans<<endl;
return 0;
}
| -------------------------------------------------------------------------------------------------- |
数学检测题,一开始用的办法是:
先检测 k 个是否符合条件
记当前的序号为 i
然后从 k+1 开始 , 每次将前 i - 1 个数按减去平均数并 abs 后的大小(即波动程度)排序 , 将差值最大的 i - 1 与 i 比较 , 若是 i 的波动更小,则替换掉 i - 1 否则往后推
但是这样做会 TLE
所以应该用复杂度更小的二分查找
方差 = 每个数^2 / n - 平均数^2.
每次二分后要在区间内排序,之后遍历每个 k 长度的区间计算方差 , 取最小 ,小则 r = mid - 1 , 大于等于则 l = mid + 1
n * log n * k 还是不够,而遍历 k 长度区间是求 和 与 平方和 , 用前缀和
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
LL a[100010],tot[100010],pown[100010],b[100010],n,k,t;
bool check(int x)
{
for(int i=1;i<=x;i++) b[i]=a[i];
sort(b+1,b+1+x);
for(int i=1;i<=x;i++)
{
tot[i]=tot[i-1]+b[i];
pown[i]=pown[i-1]+b[i]*b[i];
}
double ans=1e300;
for(int i=k;i<=x;i++)
{
//从每个 i 开始检查,一开始写了 [ x ]
ans=min(ans,((1.0*pown[i]-1.0*pown[i-k])/k)-( (1.0*tot[i]-1.0*tot[i-k]) / k )*( (1.0*tot[i]-1.0*tot[i-k]) / k ));
}
return ans<t;
}
int main() {
cin>>n>>k>>t;
for(int i=1;i<=n;i++) cin>>a[i];
int l=k,r=n,ans=-1;
while(l<=r)
{
int mid=(l+r)/2;
if(check(mid))
{
ans=mid;
r=mid-1;
}
else l=mid+1;
}
cout<<ans;
return 0;
}
| -------------------------------------------------------------------------------------------------- |
dp题
当前状态可以按如下方式摆放:
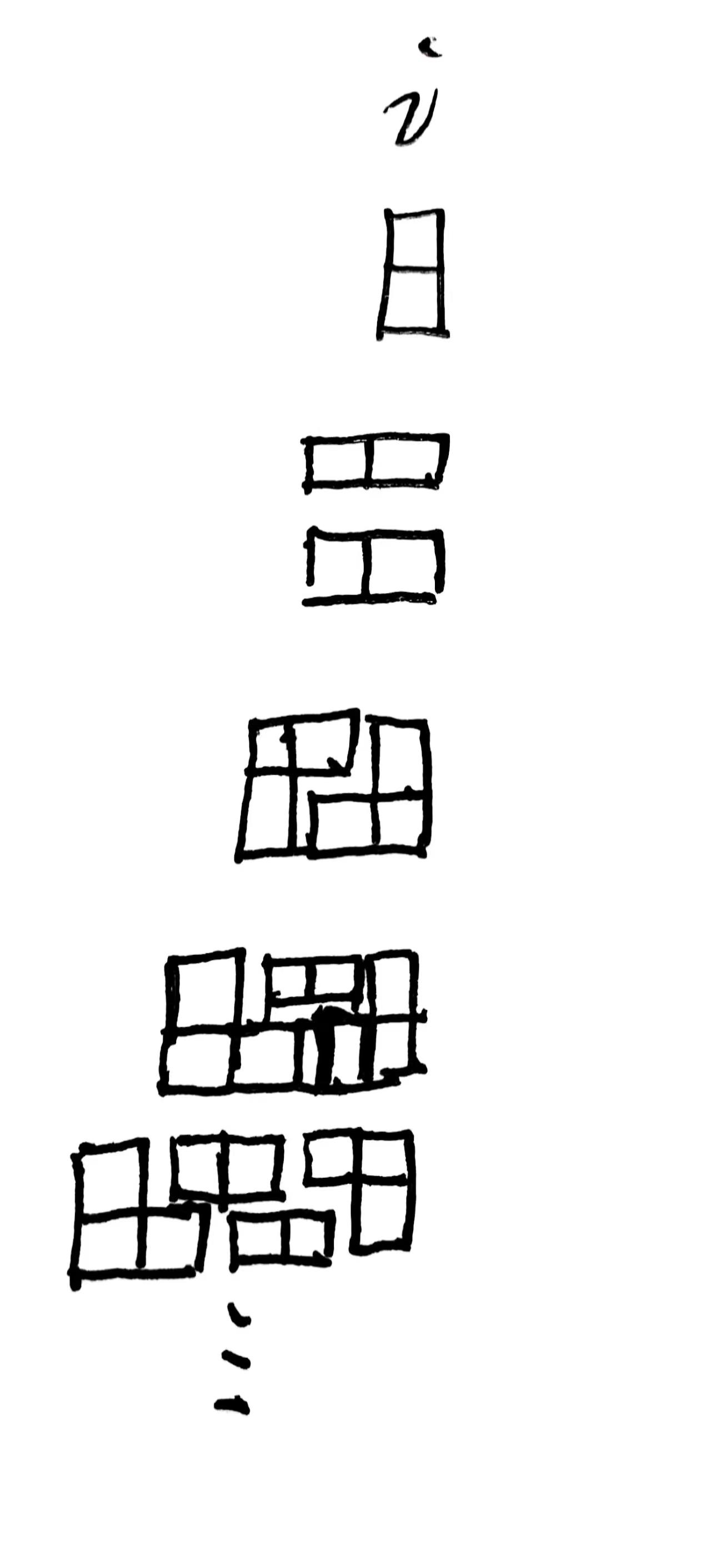
这个摆放可一直延伸到 F(0) (L型方块存在时,由于可以转动放置,方案数*2),故可得到如下推导:

然后手动dp即可
不LL,一场空
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int N=1e7+10;
LL n,mod=1000000007,ans,dp[N];
int main() {
cin>>n;
dp[1]=1,dp[2]=2,dp[3]=5;
for(int i=4;i<=n;i++)
{
dp[i]=(2*dp[i-1]%mod+dp[i-3]%mod)%mod;
}
cout<<dp[n]<<endl;
return 0;
}
| -------------------------------------------------------------------------------------------------- |
数位反转
反转操作:
int re(int a)
{
int res=0;
while(a)
{ //想象一下栈的进出,类似这种感觉
res=(res<<1)+(a&1);
a>>=1;
}
return res;
}
如果 dp 的是数的值的话,就相当于累加,可能会爆
选择 dp 反转后与原来的差值 , 最后选择最大的和最初的累加 sum 相加
当前有 转 or 不转 ,当前最大值取决于 前面转不转
如果当前 转 (1) , 则前面 不转(0) ———— i-1 的反转次数 j-1 , 转(1)———— i-1 的反转次数 j 不变
如果当前 不转(0) , 则前面 不转(0) ———— i-1 的反转次数 j , 转(1)———— i-1 的反转次数 j 不变
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
int n,m;
LL dp[1010][1010][2],t,sum,cha,d[1010];
int re(int a)
{
int res=0;
while(a)
{
res=(res<<1)+(a&1);
a>>=1;
}
return res;
}
int main() {
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>t;
sum+=t;
d[i]=re(t)-t;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
dp[i][j][0]=max(dp[i-1][j][0],dp[i-1][j][1]);
dp[i][j][1]=max(dp[i-1][j-1][0],dp[i-1][j][1])+d[i];
}
}
for(int i=1;i<=m;i++) cha=max(cha,max(dp[n][i][0],dp[n][i][1]));
//因为不一定反转后会变大,所以要遍历,看哪个最大
cout<<sum+cha;
return 0;
}
| -------------------------------------------------------------------------------------------------- |
正常思路:
每个瓜 买 | 买一半 | 买整个
买一半 ——> cnt+1
三种状态 dfs 一遍
sum == m ,ans = min ( ans , cnt )
return
如果 now == n+1 , return
优化:
当 cnt > ans ,return 剪枝
当 sum > m ,return 剪枝
但是还是 3^n 的复杂度
重点:
折半搜索
将 n 拆成两半 ,每次 dfs 其中一个
dfs 前一半时 , 到最后将 sum 与对应的 cnt 记录
dfs 后一半时 , 到最后将 sum 与前一半最后的 sum 相加 , 如果存在对应的 cnt ,则 当前cnt 与对应的 cnt 相加后,与 ans 比较 , 更新答案
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
LL n,m,ans=LLONG_MAX,a[40],N;
unordered_map <LL,LL> q;//记录折半后,一半点的 sum -- cnt 对应关系
//快读压下时间
LL read()
{
LL res=0;
char ch=getchar();
while(!isdigit(ch)&&ch!=EOF) ch=getchar();
while(isdigit(ch))
{
res=(res<<3)+(res<<1)+ch-'0';
ch=getchar();
}
return res;
}
void dfs1(int now,LL sum,LL cnt)
{
if(cnt>ans||sum>m) return;
//当前 劈瓜次数 大于 记录最小值 ,剪枝
//当前 买瓜总重量 大于 需要值 ,剪枝
if(sum==m)
{
ans=min(ans,cnt);//刚好买够,更新答案
return;
}
if(now==N+1)
{
//前提是 买瓜总重量 小于等于 需要值 , 才能记录,不然后面也没得买
if(sum<=m)
{
//将当前 买瓜重量 需要的 劈瓜次数 记录为最少那个
if(q.count(sum))
{
q[sum]=min(q[sum],cnt);
}
else q[sum]=cnt;
}
return;
}
dfs1(now+1,sum,cnt);//不买
dfs1(now+1,sum+a[now],cnt+1);//劈
dfs1(now+1,sum+(a[now]<<1),cnt);//买整个
}
void dfs2(int now,LL sum,LL cnt)
{
if(cnt>ans||sum>m) return;
if(sum==m)
{
ans=min(ans,cnt);
return;
}
if(now==n+1)
{
//如果后半段的 sum 存在一个 前半段记录的 sum 与之相加 == m ,则可以刚好买够瓜
if(q.count(m-sum))
{
ans=min(ans,q[m-sum]+cnt);
}
return;
}
dfs2(now+1,sum,cnt);
dfs2(now+1,sum+a[now],cnt+1);
dfs2(now+1,sum+(a[now]<<1),cnt);
}
int main() {
n=read(),m=read();
for(int i=1;i<=n;i++) a[i]=read();
//排序,小到大 或者 大到小,看评论好像 小到大 蓝桥官网过不了,大到小洛谷过不了
sort(a+1,a+1+n);
m<<=1;
N=n>>1;
//搜前半段
dfs1(1,0,0);
//搜后半段
dfs2(N+1,0,0);
//printf 更快,再贪一点
printf("%lld",(ans==LLONG_MAX)? -1:ans);
return 0;
}
| -------------------------------------------------------------------------------------------------- |
意思是当前节点的 兄弟节点 变为 右子节点(成一条),子节点 变成 左节点 (一个,这个节点重复以上操作)
由于 根节点 1 的兄弟节点数量是固定的 , 所以要找出 子节点中完成操作后长度最大 的子节点放在最后 , 决定深搜
不知道哪个子节点的子节点数量最大,要逐一dfs,找到最大得到,决定dp
每个节点的所有子节点数量为 该点的 size ,
最大的 子节点的子节点的数量为 该节点的 num
dp [ now ] == size + num ;
看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int N=1e5+10;
LL n,head[N],cnt,dp[N],size[N];
LL read()
{
LL res=0;
char ch=getchar();
while(!isdigit(ch)&&ch!=EOF) ch=getchar();
while(isdigit(ch))
{
res=(res<<3)+(res<<1)+ch-'0';
ch=getchar();
}
return res;
}
struct Edge{
int nxt,to,size;
}edge[N<<1];
void add(int from,int to)
{
edge[++cnt].to=to;
edge[cnt].nxt=head[from];
head[from]=cnt;
size[from]++;
}
void dfs(int now)
{
for(int i=head[now];i;i=edge[i].nxt)
{
int to=edge[i].to;
dfs(to);
dp[now]=max(dp[now],dp[to]);
}
dp[now]+=size[now];
}
int main() {
n=read();
for(int i=2;i<=n;i++)
{
int from=read();
add(from,i);
}
dfs(1);
cout<<dp[1];
return 0;
}
| -------------------------------------------------------------------------------------------------- |
波动数列
设 p == a / -b ,
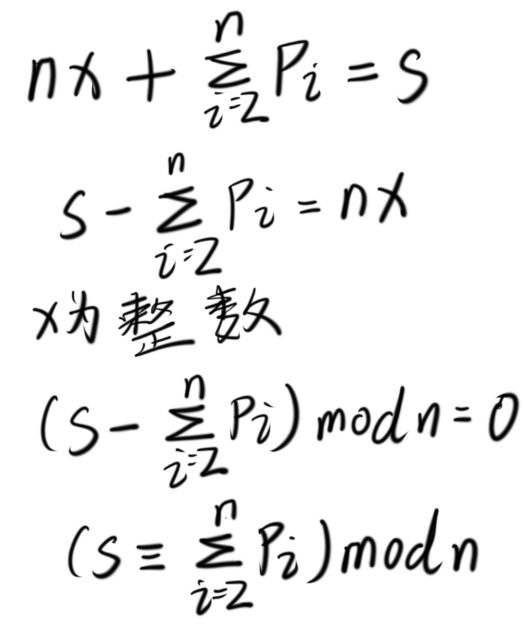
所以就要找出累加到最后,(得数 mod n) == (s mod n) 的情况的总数
而 dp 的不是当前的数,而是累加的数,所以不是 当前 的数 - /+ p ,
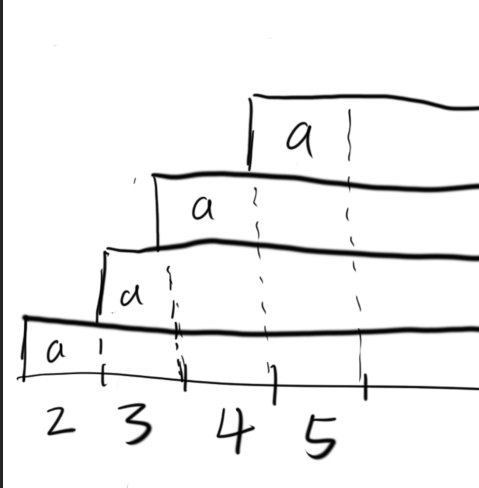
那如何 dp 总和?
看上图,总和即整个图形的面积
但是从左往右顺序 dp 的话,很难统计前面的总和,因为不知道前面具体是怎么选的,
但是从右往左 dp 的话,可以发现每次选择都会使总和加上 p*右边的长度
而当我们以右端为起点时,右边的长度就等于 i 了
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
const LL mod=1e8+7;
LL n,s,a,b,dp[1010][1010],ans;
LL read()
{
LL res=0;
char ch=getchar();
while(!isdigit(ch)&ch!=EOF) ch=getchar();
while(isdigit(ch))
{
res=(res<<3)+(res<<1)+ch-'0';
ch=getchar();
}
return res;
}
int main() {
n=read(),s=read(),a=read(),b=read();
s=(s%n+n)%n;
dp[0][0]=1;
for(int i=1;i<n;i++)
{
for(int p=0;p<=n;p++)
{
dp[i][p]=(dp[i-1][((p-i*a)%n+n)%n])%mod+(dp[i-1][((p+i*b)%n+n)%n])%mod;
}
}
ans=dp[n-1][s]%mod;
cout<<ans;
return 0;
}
| -------------------------------------------------------------------------------------------------- |
最少删除次数,即最后接龙数列的最大长度是多少
求最大长度——>dp
正常思路是:
d p [ i ] = m a x ( d p [ i - ( 前面可接龙的数的引索 ) ] + 1 , d p [ i ] )
初始化 :每个数接龙数列长度至少为 1 ,
O( n^2 ) 数据 1e5 会超时
就得优化
在往前找可接龙的数的时候,会遍历很多不可接龙的数
而 每个数的开头 ( head ) 和结尾( tail ) 都是 0 ~ 9
就可以直接 去找 tail == head 的数
将 d p 开一个第二维来找 tail == head
代码
```plaintext
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int N=1e5+3;
int n,dp[N][10];
string t;
int main() {
cin>>n;
if(n==1)
{
cout<<0<<endl;
return 0;
}
for(int i=1;i<=n;i++)
{
cin>>t;
int s=t[0]-'0',e=t[t.length()-1]-'0';
for(int j=0;j<=9;j++)
{
dp[i][j]=max(dp[i][j],dp[i-1][j]);
if(s==j) dp[i][e]=max(dp[i-1][s]+1,dp[i-1][e]);
}
}
int ans=0;
for(int i=0;i<=9;i++)
{
ans=max(dp[n][i],ans);
}
cout<<n-ans;;
return 0;
}
也可以这样考虑:
每次都是要找 (前面 tail) == (当前 head) 的数的最大长度 +1
那不就是 当前 head 的最大长度 +1 ?
处理完之后 , 当前 tail 的最大长度 不就是 max( tail 当前最长 ,当前 head 最大长度 +1 )?
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int N=1e5+3;
int n,ans;
unordered_map < int , int > dp;
void sovle()
{
cin>>n;
vector < string > a(n);
for(int i=0;i<n;i++)
{
cin>>a[i];
int s=a[i][0],e=a[i].back();
int curlen=dp[s]+1;
dp[e]=max(dp[e],curlen);
ans=max(dp[e],ans);
}
cout<<n - ans<<endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
sovle();
return 0;
}
| -------------------------------------------------------------------------------------------------- |
为什么贪心和DP会出现在同一题里啊
贪心:
按顺序找每个相邻的对
选择人数多的那个保留,另一个不要了,
因为是从左往右顺次查找
所以右边那个要保留下最佳答案来给下一个数进行选择,
所以就类似DP了?
要保留最佳答案的话
就是每次当前相比左边的大的话,就说明左边不要了,要在总数里扣除左边,正好右边比左边大,就用右边减去左边
问了一下DS,说是 i 只依赖于 i-k ,而 i-k 是已经进行更新后的最佳答案
所以应该把选择后的最佳答案放在 i ,所以要把 更新 这个操作放在 i
所以 要选择在 i 体现舍去,
左边大,就在 i 舍去, 重置为0
右边大,就在 i 舍去, i 的人数 - i-k 的人数
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int N=1e5+10;
LL n,ans,a[N],dp[N][2],k,x,h[N],cnt;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>k;
for(int i=1;i<=n;i++)
{
cin>>x;
a[x]++;
if(a[x]==1) h[++cnt]=x;
}
if(k==0)
{
cout<<cnt;
return 0;
}
sort(h+1,h+1+cnt);
for(int I=1;I<=cnt;I++)
{
int i=h[I];
if(i-k>=0)
{
if(a[i-k]<a[i])
{
a[i]=a[i]-a[i-k];
}
else
{
a[i]=0;
}
}
}
for(int I=1;I<=cnt;I++)
{
int i=h[I];
ans+=a[i];
}
cout<<ans;
return 0;
}
| -------------------------------------------------------------------------------------------------- |
把每一包糖果用二进制表示 v [ j ]
然后从 0 开始遍历每一个 状态 i ,
则 i | v [ j ] 是可以分配到的状态 ,这个状态需要的糖果包数量为 min ( dp [ i | v [ j ]
, dp [ i ] + 1 )
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int N=110,M=20,K=20;
LL n,m,k,ans,dp[1<<20],v[1<<20];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m>>k;
fill(dp,dp+(1<<20),LLONG_MAX-10);
for(int i=1;i<=n;i++)
{
int h=0,p=0;
for(int j=1;j<=k;j++)
{
cin>>p;
h|=1<<(p-1);
}
dp[h]=1;
v[i]=h;
}
for(int i=0;i<(1<<m);i++)
{
for(int j=1;j<=n;j++)
{
dp[i|v[j]]=min(dp[i|v[j]],dp[i]+1);
}
}
if(dp[(1<<m)-1]==LLONG_MAX-10)
{
cout<<-1;
}
else
{
cout<<dp[(1<<m)-1];
}
return 0;
}
纯思维题
md写了两千多长度的屎山发现写不下去一看题解四百多长度
找到 初始感冒蚂蚁 左边向右的数量 L,右边向左的数量 R
如果 初始感冒蚂蚁向左
如果 L == 0
则 ans == 1
如果 L != 0
ans = L + R + 1
可以想象一下牛顿摆那种感觉,碰撞后反弹可视作两个物体穿过了彼此(速度始终不变且都等于同一个常数 1 )
点击查看代码
#include <bits/stdc++.h>
typedef long long int LL;
using namespace std;
const int N=1e5+10;
LL n,m,a[N],ans,l,r;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=2;i<=n;i++)
{
if(abs(a[i])<abs(a[1])&&a[i]>0) l++;
else if(abs(a[i])>abs(a[1])&&a[i]<0) r++;
}
if(a[1]<0)
{
if(l==0) ans=1;
else ans=l+r+1;
}
else if(a[1]>0)
{
if(r==0) ans=1;
else ans=l+r+1;
}
cout<<ans;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号