欧拉降幂 super_log

求 (a ^ a ^ a... ^ a) mod p,b个a的幂塔

 

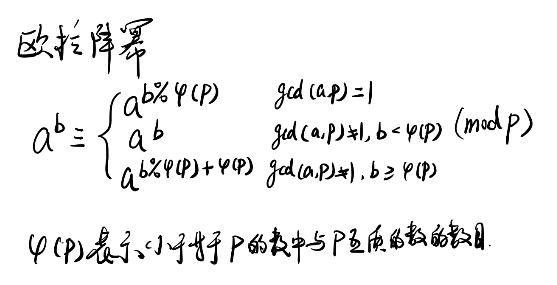
https://nanti.jisuanke.com/t/41299 

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<stack>
#include<cstdlib>
#include<queue>
#include<set>
#include<string.h>
#include<vector>
#include<deque>
#include<map>
using namespace std;
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define eps 1e-4
#define bug printf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]" <<endl


typedef long long LL;
typedef long long ll;
const int maxn = 1e5 + 5;


#define Mod(a,b) a<b?a:a%b+b    //重定义取模，按照欧拉定理的条件
LL gcd (LL a,LL b) {
    return b == 0 ? a : gcd(b,a % b);
}
LL fpow(LL x,LL n,LL mod) {
    LL res = 1;
    while (n) {
        if (n & 1) res = Mod(res * x, mod), n--;
        x = Mod(x * x, mod);
        n >>= 1;
    }
    return res;
}

LL phi(LL x) {  //求互质个数
    LL ans = x;
    for (int i = 2; i * i <= x; i++) {
        if (x % i == 0) {
            ans = ans / i * (i - 1);
            while (x % i == 0) x /= i;
        }
    }
    if (x != 1) ans = ans / x * (x - 1);
    return ans;
}

LL solve(LL a,LL b,LL m) {
    if(m == 1) return 0;
    if(b <= 1) return fpow(a,b,m);
    LL p = phi(m);
    LL t = solve(a,b - 1,p);
    LL g = gcd(a,m);
    if(g == 1 || b < p) return fpow(a,t,m); //符合欧拉降幂的gcd(a,p) = 1 || b < phi(p)
    else return fpow(a,t + p,m);        //另一种
}

int main() {
    int t;
    cin >> t;
    while (t--) {
        LL a,b,m;
        scanf("%lld %lld %lld",&a,&b,&m);
        printf("%lld\n",solve(a,b,m) % m);
    }
    return 0;
}