3.5 归并排序的java实现

文章目录

• 归并排序
• • 1.基础理论
  • • 1.1 基本描述
  • 2. Java代码实现

归并排序

1.基础理论

1.1 基本描述

归并排序以最坏时间复杂度O(N log N)运行，它所使用到的比较次数几乎是最优的，它是递归算法的一个很好的实例。

这个排序算法中基本的操作就是合并两个已经排序的表。

因为输入的两个表是已排序的，所以若将输出放到第三个表中， 则该算法可以通过对输入数据一趟排序来完成。

合并算法图示如下：

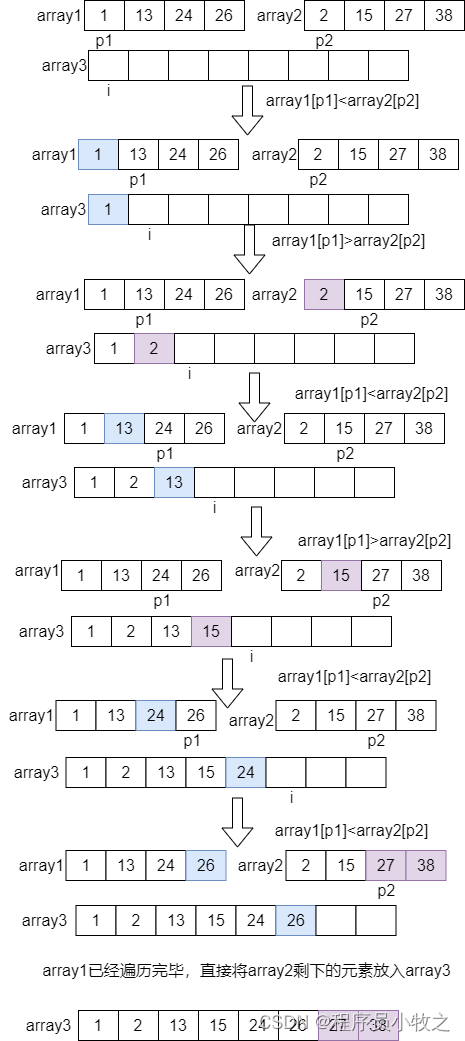
所以归并排序算法的步骤描述为：

如果N=1,那么只有一个元素直接返回结果，否则递归的将前本部分数据和后半部分数据各自归并排序，

得到排序后的两部分数据，然后使用上面描述的合并算法再将这两部分合并到一起。

也就是说最小子问题就是N=2

例如:

我们想将这个数组{24,13,26,1,2,27,38,15}排序，

我们递归的将前四个数据和后四个数据分别排序，得到
{24},{13},{26},{1},{2},{27},{38},{15},

然后使用归并方法对{24} {13} 进行归并得到{13,24}

对{26} {1} 进行归并得到{1,26}

对{2},{27} 进行归并得到{2,27}

对{38},{15} 进行归并得到{15,38}

接着对 {13,24} ,{1,26}进行归并得到{1,13,24,26}

对{2,27},{15,38}进行归并得到{2,15,27,38}

最后 我们将{1,13,24,26},{2,15,27,38}这两部分进行合并，最后得到{1,2,13,15,24,26,27,38}

该算法使用了经典的分治策略, 它将问题分成一些小的问题然后递归求解。

2. Java代码实现

class Test{
    /**
     * 合并两个已经排好序的数组
     * @param a
     * @param left
     * @param mid
     * @param right
     */
    public static void merge(int[] a, int left,int mid,int right) {

        int[] result = new int[right-left+1];

        // p1,p2是检测指针， index是存放指针
        int p1 = left, p2 = mid+1, index = 0;
        // 执行双数组元素比较
        while (p1<=mid&&p2<=right) {
            if(a[p1]<=a[p2]){
                result[index++] = a[p1++];
            }
            else{
                result[index++] = a[p2++];
            }
        }

        while (p1<=mid) result[index++] = a[p1++];
        while (p2<=right) result[index++] = a[p2++];

        System.arraycopy(result, 0, a, left, result.length);

    }

    /**
     * 归并排序，采用分治，递归思想
     * @param a
     * @param start
     * @param end
     */
    public static void mergeSort(int[] a,int start,int end) {
        if(start < end){
            int mid = (start+end)/2;
            mergeSort(a,start,mid);
            mergeSort(a,mid+1,end);
            merge(a,start,mid,end);
        }
    }

    public static void mergeSortTest() {
        int[] numbs = {24,13,26,1,2,27,38,15};
        mergeSort(numbs,0,numbs.length-1);
        System.out.println(Arrays.toString(numbs));
    }

    public static void main(String[] args) {
        mergeSortTest();
    }
}

运行结果：