机器学习—线性回归

一、原理部分：

只能图片形式展现了~~~

 

二、利用sklearn完成：

1、linear_regression

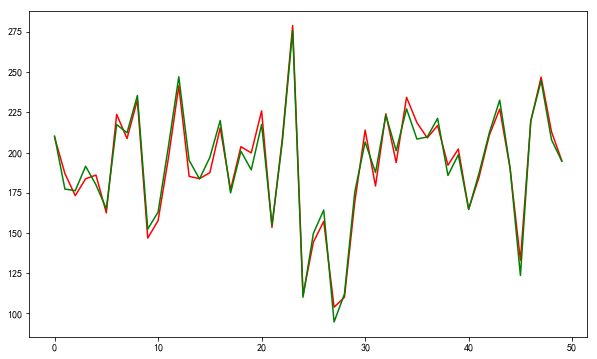
# -*- coding: utf-8 -*-
"""

最简单的线性回归例子，直接通过制造的一些数据来做拟合，效果不错

"""
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

#制造一些数据
x_data = np.random.rand(200,5)*10
w = np.array([2,4,6,8,10])
y = np.dot(x_data,w) + np.random.rand(200)*20 + 20

#训练数据
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

linreg = LinearRegression()
x_train,x_test,y_train,y_test = train_test_split(x_data,y,random_state = 0)
linreg.fit(x_train,y_train)
print(linreg.coef_,linreg.intercept_)
y_hat = linreg.predict(x_test)
print('均方误差是：',mean_squared_error(y_test,y_hat))

#画图
fig,ax = plt.subplots()
fig.set_size_inches(10,8)
ax.plot(np.arange(len(y_hat)),y_hat,color = 'r')
ax.plot(np.arange(len(y_hat)),y_test,color = 'g')

实际的值是2，4，6，8，10，20

[ 2.1273754 4.04650716 6.2226947 8.1097271 9.70858232] 28.9951381971
均方误差是： 32.1167408823

2、lasso 和 ridge

#lasso
from sklearn.linear_model import Lasso
from sklearn.model_selection import GridSearchCV

lasso = Lasso()
model_lasso = GridSearchCV(lasso,param_grid=({'alpha':np.linspace(0.01,0.1,10)}),cv=5)
model_lasso.fit(x_train,y_train)
print('lasso最佳参数',model_ridge.best_params_)
y_hat = model_lasso.predict(x_test)
print('lasso方误差是:',mean_squared_error(y_hat,y_test))

#ridge
from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV

ridge = Ridge()
model_ridge = GridSearchCV(ridge,param_grid=({'alpha':np.linspace(0.01,0.1,10)}),cv=5)
model_ridge.fit(x_train,y_train)
print('ridge最佳参数',model_ridge.best_params_)
y_hat = model_ridge.predict(x_test)
print('ridge方误差是:',mean_squared_error(y_hat,y_test))

 

[ 1.94244827 4.13058413 5.95265804 8.11566939 9.83600987] 30.2444896465
linreg均方误差是： 27.7224828081

lasso最佳参数 {'alpha': 0.01}
lasso方误差是: 27.7329662439

ridge最佳参数 {'alpha': 0.01}
ridge方误差是: 27.7230576859

 

3、logistic regression

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV

#载入数据
digits = load_digits()
x_data = digits.data
y_data = digits.target
x_train,x_test,y_train,y_test = train_test_split(x_data,y_data)
lr = LogisticRegression()
lr.fit(x_train,y_train)
y_hat = lr.predict(x_test)
print('正确率:',accuracy_score(y_hat,y_test))

#logistic regression 自带l2正则，所以有一个参数C可以调参
model_lr = GridSearchCV(lr,param_grid=({'C':np.linspace(0.01,0.1,10)}),cv=5)
model_lr.fit(x_train,y_train)
print('最佳的参数是：',model_lr.best_params_)
y_hat = model_lr.predict(x_test)
print('误差是',accuracy_score(y_hat,y_test))

 

错误率: 0.951111111111

调参之后略有所提升吧，意义不大

最佳的参数是： {'C': 0.070000000000000007}
误差是 0.953333333333

三、Python手工实现线性回归

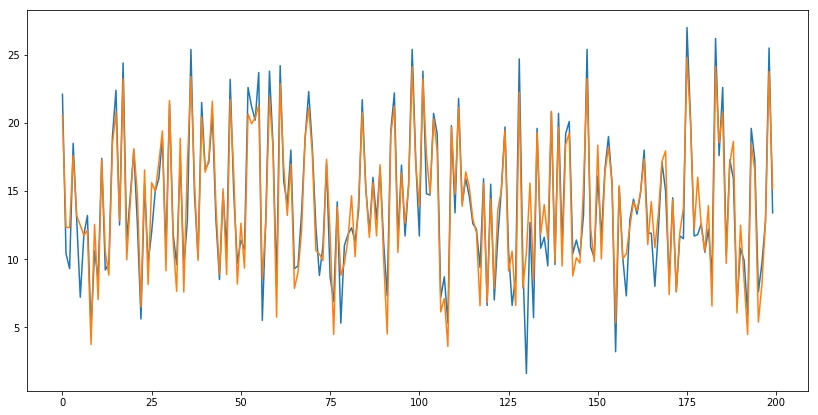
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

class linear_regression(object):

    #计算均方误差损失        
    def compute_loss(self,y,y_hat):
        return np.average((y-y_hat)**2)
    
    #梯度下降算法
    def compute_gradient(self,n,x,y):
        x['temp']=1
        w = np.zeros(len(x.columns))
        for i in range(n):
            w -= 0.00001*np.dot(x.T,(np.dot(x,w)-y))
        return w
    
    #数据标准化
    def stand_data(self,x):
        return (x-x.mean())/x.std()
    
    #作图
    def plot_data(self,y,y_hat):
        fig,ax = plt.subplots()
        fig.set_size_inches(14,7)
        ax.plot(np.arange(len(y)),y)
        ax.plot(np.arange(len(y_hat)),y_hat)
    
    
if __name__ == '__main__':
    data = pd.read_csv('data.csv')
    x = data.iloc[:,1:-1]
    y = data.iloc[:,-1]
    lin_reg = linear_regression()
    #数据标准化
    x = lin_reg.stand_data(x)
    #标准化后求参数，在求参数过程中，自动给x增加一列偏移项1
    w = lin_reg.compute_gradient(10000,x,y)
    print('参数值：',w)
    #预测值
    y_hat = np.dot(x,w)
    #计算均方误差
    ls = lin_reg.compute_loss(y,y_hat)
    print('均方误差：',ls)
    #画图
    lin_reg.plot_data(y,y_hat)

参数值： [ 3.92908866 2.7990655 -0.02259148 14.02249997]
均方误差： 2.78412631453