详细介绍：人工智能系统学习之 FastAi 学习笔记（二）-卷积神经网络（CNN）

卷积神经网络（CNN）

概念	作用
特征工程	转换输入数据，让模型更容易提取模式。
卷积	自动提取图像的局部特征，如边缘、角点、纹理。
卷积核	一个小矩阵（如 3×3），负责扫描图像并计算特征。
CNN 价值	免去手动设计图像特征，让模型直接从数据中学习。

1、核心概念“卷积”的基本思想

1️⃣ 卷积神经网络（CNN）概述

CNN 是一种专门用于图像识别的神经网络结构。
它通过卷积操作提取图像中的关键特征（例如边缘、纹理），而不需要手动设计复杂的特征工程。
fastai 提供了许多内置工具，可以轻松构建 CNN 模型，实现高精度图像分类。

2️⃣ 特征工程（Feature Engineering）

特征工程是机器学习中一个重要概念：
通过对输入数据做转换来生成更适合模型的特征。
在表格数据中，我们可能会添加日期特征（如 add_datepart）。
在图像中，特征通常是一些视觉上显著的模式，例如边缘、角点、纹理。

3️⃣ 图像中的特征

以数字识别为例：
数字 7 的特征：顶部的水平边缘 + 右上到左下的对角边。
数字 3 的特征：左上和右下的对角边 + 中间及上下的水平边缘。
CNN 的目的就是自动提取这些特征，而不需要人工标注。

4️⃣ 卷积（Convolution）的原理

卷积是提取图像特征的核心操作。
卷积的核心是一个卷积核（kernel），例如 3x3 的小矩阵。
核心运算步骤：
卷积核在图像上滑动（扫描）。
对覆盖的区域执行元素相乘并求和。
输出的结果是新的“特征图”（feature map）。
卷积能够自动检测图像中的边缘、线条等局部特征，是 CNN 强大表现的根基。

2、数学计算原理

卷积与卷积核 (Kernel)

卷积 (Convolution)：一种用小矩阵（卷积核或滤波器）在图像上滑动并进行运算的操作。
卷积核 (Kernel)：例如一个 3×3 的权重矩阵，会与图像的每一个 3×3 区域对应元素相乘，再把结果相加，得到一个新的数值，构成输出特征图。

边缘检测的例子：Top Edge Filter

示例卷积核：

top_edge = tensor([[-1,-1,-1],
[ 0, 0, 0],
[ 1, 1, 1]]).float()

上方的 -1 表示“减去上边像素”
下方的 1 表示“加上下边像素”
中间 0 表示忽略中间行
作用：检测水平边缘。
当图像某处上方亮度低、下方亮度高时（由亮到暗的过渡），卷积结果是一个大正数。
如果上下亮度相近，结果接近 0。
例子：

(im3_t[4:7,6:9] * top_edge).sum()  # 计算位置(5,8)
# 结果 tensor(762.)

说明这里是一个显著的上边缘（数值越大表示越符合边缘特性）。

更复杂的应用

改变 kernel 的形状可以检测不同特征，比如：
左边缘（竖直边缘）
斜线
模糊、锐化等

在深度学习的卷积神经网络（CNN）中，这些 kernel 会在训练中自动学习，而不是手工设定。

代码要点与流程

卷积kernel

取样图像并转为张量

im3 = Image.open(path/'train'/'3'/'12.png')
im3_t = tensor(im3)

卷积计算

(im3_t[4:7,6:9] * top_edge).sum()

选取局部区域并做逐元素乘积求和。
封装函数便于复用

def apply_kernel(row, col, kernel):
return (im3_t[row-1:row+2, col-1:col+2] * kernel).sum()

例如 apply_kernel(5,7,top_edge)。

卷积操作（取特征）

假设输入数据 xb：
一批 64 张图片
每张图片是单通道（灰度图）
每张图片大小 28×28
所以形状是 [64, 1, 28, 28]

卷积核 edge_kernels：
一共 4 个卷积核（检测不同方向的边）
每个卷积核的大小 3×3
单通道输入
所以形状是 [4, 1, 3, 3]

batch_features = F.conv2d(xb, edge_kernels)

PyTorch 一次把这 4 个卷积核应用到 64 张图片的每一张上。
输出形状是 [64, 4, 26, 26]
输出的 4 个维度含义：
64：保留输入的批大小（每张图片都会得到对应输出）
4：因为有 4 个卷积核，每个卷积核产生一个特征图
26×26：卷积后的空间尺寸
为什么从 28×28 变成了 26×26？是因为卷积大小是 3×3，没有 padding，步长是 1。
out_height = (28 + 20 - 3)/1 + 1 = 26
out_width = (28 + 20 - 3)/1 + 1 = 26

PyTorch 的强大之处：

一次操作多个图片：批处理（batch），这里是 64 张。
一次操作多个卷积核：4 个卷积核。
一次操作多通道：例如彩色图可以有 RGB 三个通道。
同时利用 GPU 并行运算：如果不并行，而是一张图一个卷积核地做，需要几百倍乃至上千倍的时间。

界像素的“丢失”和 padding：

因为没有填充（padding），卷积核在最外一圈无法完整覆盖，导致每个方向上都少了 2 个像素（上少 1 行，下少 1 行；左少 1 列，右少 1 列），所以从 28×28 缩小到 26×26。
解决办法：
设置 padding=1，即在图像四周补上一圈 0：

F.conv2d(xb, edge_kernels, padding=1)

这样输出大小就能保持和输入一致（28×28）。

为什么需要Padding（填充）？

当 kernel（卷积核）在输入图像上滑动时，靠近图像边缘的像素被“利用得不够充分”，因为卷积核无法超出图像边界。
例如：一个 5×5 图像，用 3×3 kernel 卷积后，输出是 3×3，比原图小。
这样每次卷积都会让图像缩小，如果层数多，图像很快就会变成非常小的矩阵。
解决办法：Padding
在图像四周补充额外的像素（一般补 0），这样可以保证卷积核能覆盖到边缘像素。
效果：
如果我们希望输出大小和输入保持一致（最常见），那么需要在四周补 ks//2 个像素（ks 是 kernel 大小）。
比如 3×3 kernel → padding = 1
输入 5×5 → 输出 5×5（保持大小不变）。

Stride（步幅）

默认 stride = 1：卷积核每次移动 1 个像素。
stride > 1：卷积核每次跨更大的步长，跳跃式地采样。
例如 stride = 2，相当于“下采样”，输出的尺寸会更小。
常用于降低空间维度，减少计算量。

输出大小公式

对于输入大小 n（可以是高度 h 或宽度 w），卷积输出大小的计算公式是：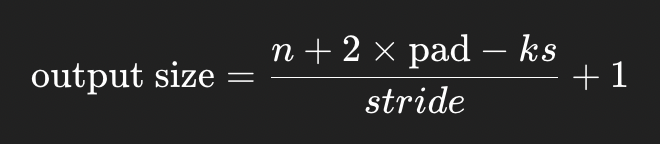

其中：
n = 输入大小（h 或 w）
pad = padding 的大小
ks = kernel 的大小
stride = 步幅

卷积等式的理解：

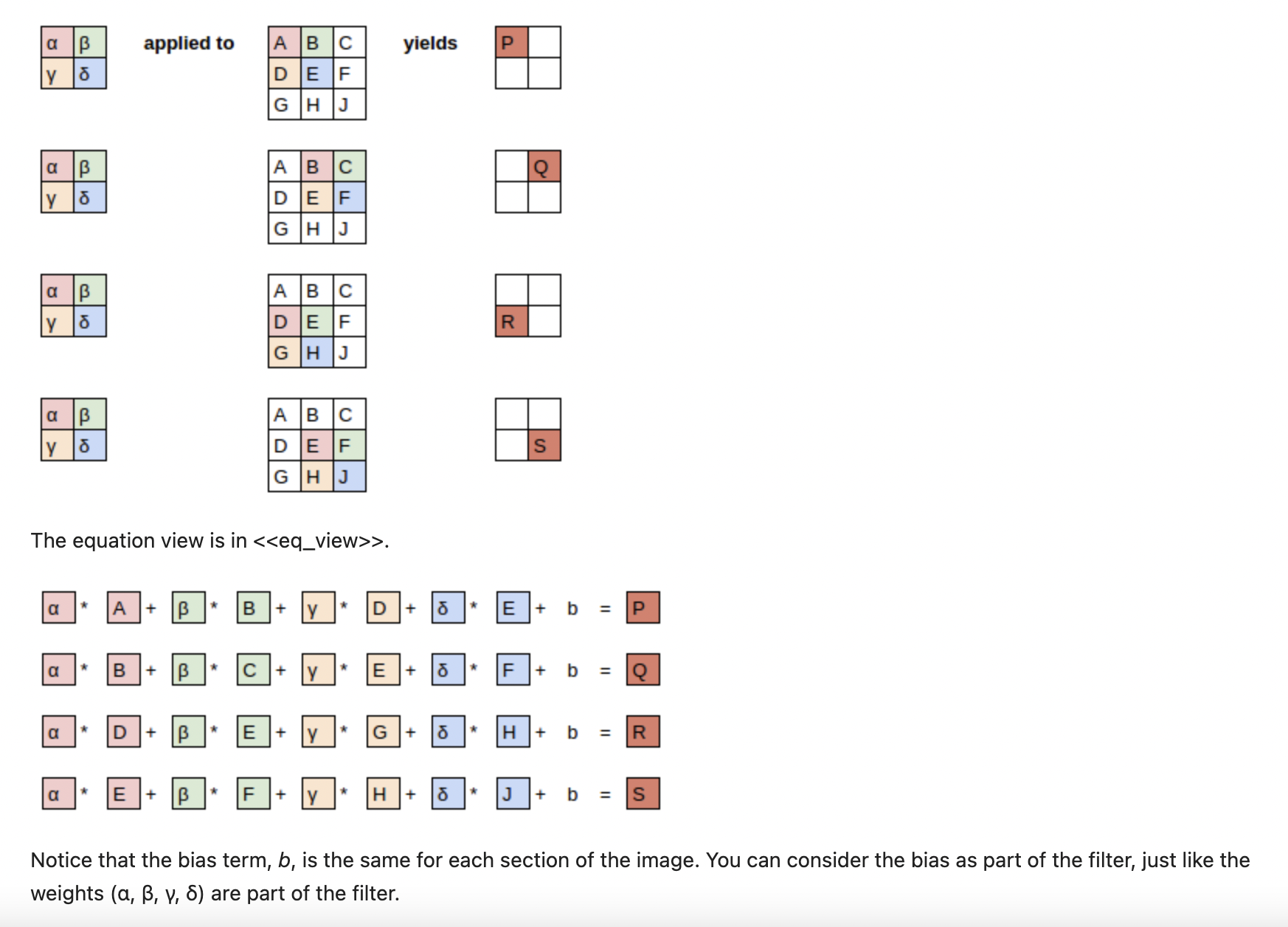
把卷积写成矩阵乘法的形式：
输入图像的像素排成一个向量：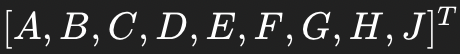

卷积核被“展开”成一个稀疏矩阵（很多位置是 0），然后乘以上面的输入向量，再加上偏置 b
这样，就可以把卷积看成是一种特殊的矩阵乘法。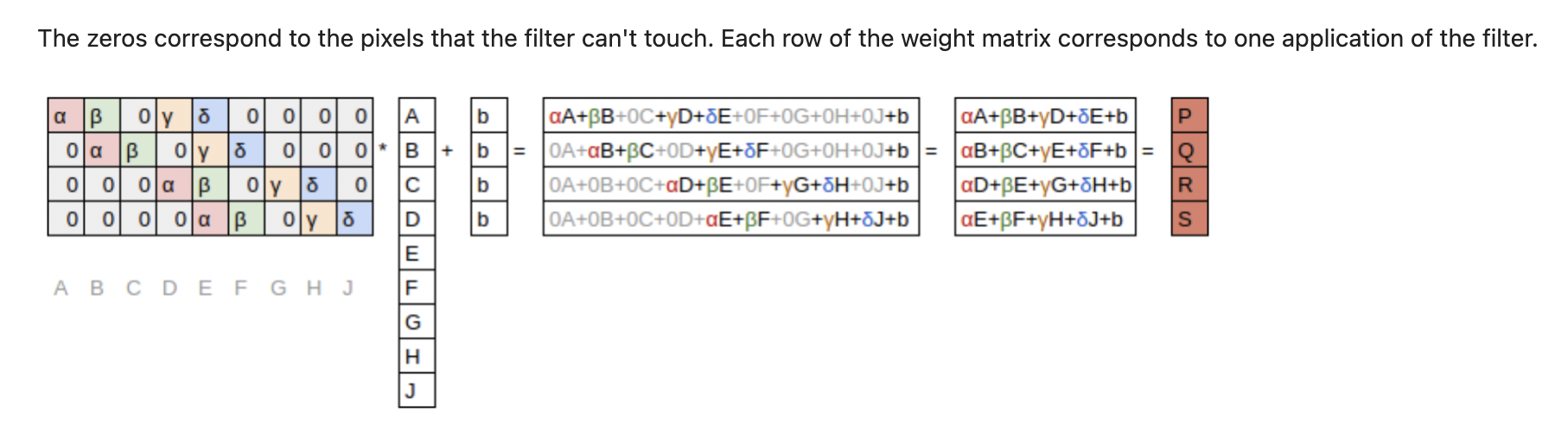

特殊性质：

• 共享权重（Shared Weights）
  不同位置的卷积操作，卷积核参数α,β,γ,δ 都是一样的。
  这和全连接层（每个位置都有独立权重）不同，大大减少了参数数量。
• 稀疏连接（Sparse Connections）
  每次卷积只覆盖输入的一小部分（局部感受野），不像全连接层那样和所有输入相连。

3、第一个CNN卷积神经网络

回顾：nn.Linear 是什么

nn.Linear 是 PyTorch 里的 全连接层（Fully Connected Layer, FC），也叫 线性层。它的功能就是做一个线性变换：

nn.Linear(in_features, out_features, bias=True)

in_features：输入向量的维度（多少个输入神经元）
out_features：输出向量的维度（多少个输出神经元）
bias：是否加上偏置项（默认为 True）
例如：

import torch
import torch.nn as nn
# 定义一个 Linear 层：输入是 4 维，输出是 2 维
fc = nn.Linear(4, 2)
# 输入一个 batch，batch_size=3，每个样本是 4 维
x = torch.randn(3, 4)
# 前向传播
y = fc(x)
print(y.shape)   # torch.Size([3, 2])

这表示：
输入每个样本是 4 维
经过 Linear(4,2) 变成 2 维
对 batch 中 3 个样本一起处理，输出形状就是 [3,2]
总结：
nn.Linear 就是一个 矩阵乘法 + 加偏置 的操作。
它把输入向量从一个维度映射到另一个维度，相当于神经元之间的全连接。

nn.Conv2d

输入：(batch=64, channels=1, height=28, width=28)
卷积层：nn.Conv2d(1, 30, kernel_size=3, padding=1)
输出：(64, 30, 28, 28)
这里的 30 来自 out_channels，不是图像大小。
图像大小还是28*28

nn.Conv2d(in_channels, out_channels, kernel_size, padding, stride)

in_channels：输入图像的通道数
灰度图像是 1 通道
彩色 RGB 图像是 3 通道
out_channels：卷积层要学习的 卷积核数量（feature maps 的数量）
这里的 30 就表示会学习 30 个 3×3 的卷积核
每个卷积核都会扫描整张输入图像，提取不同的特征（比如边缘、纹理、曲线等）
输出时就会得到 30 张 feature map，因此输出通道数是 30
kernel_size=3：卷积核大小是 3×3
padding=1：在图像四周补 1 像素（保持输出大小不变）
stride=1（默认）：卷积核每次移动 1 像素

broken_cnn

broken_cnn = sequential(
nn.Conv2d(1, 30, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(30, 1, kernel_size=3, padding=1)
)

输入：28×28 灰度图（channel=1）
第 1 个 Conv2d：输入通道=1（图像通道数），输出通道=30，kernel=3×3，padding=1，这里30可以理解为30个特征kernel
ReLU：不改变形状
第 2 个 Conv2d：输入通道=30，输出通道=1，kernel=3×3，padding=1

一个简单CNN

先定义一个转换函数conv：

def conv(ni, nf, ks=3, act=True):
res = nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)
if act:
res = nn.Sequential(res, nn.ReLU())
return res

创建了一个 卷积层，输入通道 ni，输出通道 nf
卷积核大小 ks（默认为 3）
步长 stride=2 → 输出尺寸减半
padding=ks//2 → 保持特征图大小相对稳定（对称填充）

创建一个简单CNN：

simple_cnn = sequential(
conv(1 ,4),            #14x14
conv(4 ,8),            #7x7
conv(8 ,16),           #4x4
conv(16,32),           #2x2
conv(32,2, act=False), #1x1
Flatten(),
)

每层的含义

1️⃣ conv(1, 4) → 输出 14×14
输入：1 通道（灰度图 28×28）
卷积核数量：4 → 输出 4 个特征图
stride=2 → 尺寸减半：28×28 → 14×14
结果：输出形状 = (batch, 4, 14, 14)

2️⃣ conv(4, 8) → 输出 7×7
输入：4 通道
输出：8 通道（8 个特征图）
尺寸：14×14 → 7×7
结果：输出形状 = (batch, 8, 7, 7)

3️⃣ conv(8, 16) → 输出 4×4
输入：8 通道
输出：16 通道
尺寸：7×7 → 4×4
结果：(batch, 16, 4, 4)

4️⃣ conv(16, 32) → 输出 2×2
输入：16 通道
输出：32 通道
尺寸：4×4 → 2×2
结果：(batch, 32, 2, 2)

5️⃣ conv(32, 2, act=False) → 输出 1×1
输入：32 通道
输出：2 通道
尺寸：2×2 → 1×1
注意：这里 act=False → 不加 ReLU，最后一层直接保留卷积结果
结果：(batch, 2, 1, 1)

6️⃣ Flatten()
把 (batch, 2, 1, 1) 展平为 (batch, 2)
相当于得到了一个 2 维的输出向量（可以对应二分类任务的两个类别分数）

总体结构
输入：(batch, 1, 28, 28)
输出：(batch, 2)
这其实就是一个完整的 CNN 分类网络：
多层卷积 + ReLU：逐层提取特征，通道数增加，空间尺寸缩小
最后卷积到 1×1：相当于全局特征提取
Flatten：变成一个小向量（这里是 2 维）作为最终输出

simple_cnn(xb).shape
torch.Size([64, 2])
learn = Learner(dls, simple_cnn, loss_func=F.cross_entropy, metrics=accuracy)
learn.summary()
Sequential (Input shape: ['64 x 1 x 28 x 28'])
================================================================
Layer (type)         Output Shape         Param #    Trainable 
================================================================
Conv2d               64 x 4 x 14 x 14     40         True
________________________________________________________________
ReLU                 64 x 4 x 14 x 14     0          False
________________________________________________________________
Conv2d               64 x 8 x 7 x 7       296        True
________________________________________________________________
ReLU                 64 x 8 x 7 x 7       0          False
________________________________________________________________
Conv2d               64 x 16 x 4 x 4      1,168      True
________________________________________________________________
ReLU                 64 x 16 x 4 x 4      0          False
________________________________________________________________
Conv2d               64 x 32 x 2 x 2      4,640      True
________________________________________________________________
ReLU                 64 x 32 x 2 x 2      0          False
________________________________________________________________
Conv2d               64 x 2 x 1 x 1       578        True
________________________________________________________________
Flatten              64 x 2               0          False
________________________________________________________________
Total params: 6,722
Total trainable params: 6,722
Total non-trainable params: 0
Optimizer used: <function Adam at 0x7fbc9c258cb0>
  Loss function: <function cross_entropy at 0x7fbca9ba0170>
    Callbacks:
    - TrainEvalCallback
    - Recorder
    - ProgressCallback

learn.fit_one_cycle(2, 0.01)
epoch	train_loss	valid_loss	accuracy	time
0	0.072684	0.045110	0.990186	00:05
1	0.022580	0.030775	0.990186	00:05

4、神经网络优化及观察

感受视野（Receptive Field）

1. 感受野（Receptive Field）的直观比喻
   你可以把 CNN 想成一个“观察者”：
   第一层卷积：眼睛只能看到一小块（比如 3×3）的区域。
   第二层卷积：虽然它还是“看 3×3”，但它看的对象是上一层的特征。而上一层的一个点，其实已经代表了原始图像的 3×3，所以第二层“间接”看到的是更大范围（比如 7×7）。
   第三层卷积：再叠一层，能看到的范围就更大了（比如 15×15）。
   这样一层层堆下去，越往后的神经元，能看到输入图像的范围就越大，直到最后几乎覆盖整张图。
2. 数学规律
   如果每一层卷积核大小是 ，步幅 stride 是
   第一层感受野：
   第二层感受野：上一层感受野 × stride + (kernel_size - 1)
   第三层感受野：再套一次这个公式
   …

例子：
输入图像 28×28，每层卷积核 3×3，stride=2。
Conv1 → 感受野 = 3
Conv2 → 感受野 = 3×2 + (3-1) = 8（严格推算是 7，但大概就是比 3 大很多）
Conv3 → 再扩大，能看到 15×15
Conv4 → 扩大到 31×31，几乎整张图了

第 层的感受野严格公式：



Π这个符号是 连乘积符号（Π，Pi notation），和求和的 Σ 很像，但它表示的是乘法而不是加法。

3. 为什么重要？
   浅层卷积 → 只能提取小的局部特征（边缘、角点）
   深层卷积 → 感受野更大，能理解更复杂的模式（比如一条腿、一张脸）
   最后几层 → 感受野足够大，能看到整张图，做整体分类（比如“这是个数字 7”）。

画图查看数据

把图像的三个通道、三个子图位置、三个颜色映射规则一一配对，然后在循环里一次性画出来。

im = image2tensor(Image.open(image_bear()))
im.shape
torch.Size([3, 1000, 846])
show_image(im);  #显示一张图
_,axs = subplots(1,3) #1行3列的画图
for bear,ax,color in zip(im,axs,('Reds','Greens','Blues')):
show_image(255-bear, ax=ax, cmap=color) #显示3张图

zip用法：

zip(a, b, c) 会把多个序列「打包」在一起。
它会同时从 a、b、c 中各取一个元素，组成一个元组 (a[i], b[i], c[i])。
最终循环时，就会一次次得到这些三元组。
举个小例子：
for x, y, z in zip([10,20,30], [‘A’,‘B’,‘C’], [‘R’,‘G’,‘B’]):
print(x, y, z)
输出：
10 A R
20 B G
30 C B

show_image基本用法

show_image(image, ax=None, **kwargs)

参数解释

image: 输入的图像数据。通常是一个 Tensor（例如，形状为 (C, H, W)，表示通道、宽度和高度）或 PIL 图像。可以是单通道（灰度图像）或者多通道（RGB图像）。

ax: 可选参数。指定绘图的子图（matplotlib 的 Axes 对象），如果没有提供，默认会创建新的图像。

kwargs: 其他额外的参数，可能用于控制图像显示的行为，例如颜色映射（cmap）、标题（title）等。

常见激活函数

激活函数	数学表达式	图形特征	主要作用
ReLU	( f(x) = \max(0, x) )	小于0变0，大于0保持原样	计算快、梯度不消失，是最常用的
Sigmoid	( f(x) = \frac{1}{1 + e^{-x}} )	输出范围(0,1)	常用于二分类输出层
Tanh	( f(x) = \tanh(x) )	输出范围(-1,1)	常用于隐藏层（已被ReLU取代）
Softmax	( f_i(x) = \frac{e^{x_i}}{\sum_j e^{x_j}} )	转成概率分布	用于多分类的最后一层

“激活值”的作用

“激活值”就是每个神经元在经过激活函数后的输出结果
在训练时，模型会不断更新权重 ，
而每一层的输出（激活值）就会告诉我们网络“活不活着”。
如果激活值：
太大 → 梯度爆炸（数值发散）
太小 → 梯度消失（模型学不动）
全是 0 → 网络死掉（尤其 ReLU）

所以我们要监控：
激活的平均值（mean）
标准差（std）
有多少接近 0（% near zero）

指标	含义	说明
mean	激活平均值	应该在 0 附近
std	激活标准差	不应太大或太小
% near zero	接近 0 的比例	太高说明神经元“死掉”

1cycle Training

1cycle 是一种 学习率调度策略，由 Leslie Smith 提出。
它的思想是：不固定学习率，而是在训练过程中先上升再下降。FastAI 提供了便捷函数：

learn.fit_one_cycle(epochs, lr_max)

阶段	原因
低学习率开始	防止初期发散（权重太乱）
中高学习率阶段	训练更快、能跳出坏的局部极小值
再降低学习率	让模型稳定下来，防止震荡、提高泛化性

训练效果可视化

learn.activation_stats.color_dim(-2)

展示整个训练过程中激活分布随 batch 的变化情况。
横轴：训练 batch
纵轴：激活值范围
颜色：激活值出现的密度（亮 = 多）
解释图像：
左侧暗蓝 → 激活接近 0（模型刚开始，几乎没激活）
黄色上升 → 激活开始分布到更广范围（模型开始学习）
如果黄色部分反复出现和坍塌（collapse） → 表示训练不稳定，激活周期性爆炸又塌陷。

为什么会 collapse？
激活值反复爆炸又归零，常见原因有：
学习率过高（1cycle 未调好）
没有批标准化（BatchNorm）
权重初始化不平衡
ReLU 截断过多
解决方案：
使用 Batch Normalization
使用 1cycle 调度 让激活分布平滑变化
检查 learning rate finder 选择合适的 lr_max

Batch Normalization

Batch Normalization 解决的问题：内部协变量偏移（Internal Covariate Shift）

问题背景：

在训练神经网络时，每一层的输入分布会不断变化：
因为前一层的参数在训练中不断更新。
这样会导致：
后面层的输入分布不停变化；
网络不得不“重新适应”这些变化；
训练变慢、甚至不稳定；
必须使用更小的学习率和精心初始化。
这种现象就叫：
内部协变量偏移（Internal Covariate Shift）

BatchNorm 让每一层的输入“先归一化再微调”。
它既保证训练稳定（通过归一化），又保持模型灵活（通过 γ 和 β）。
BN 的三步核心操作：

第 1 步：计算当前 batch 的均值和标准差

这就相当于“看这一批数据整体的分布中心和离散程度”。

第 2 步：标准化每个激活

用刚算出来的均值 μ 和标准差 σ，把每个激活值拉到同一标准上：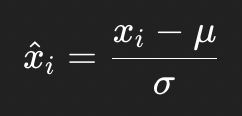

意思是：
减去均值（中心化），让整体平均值变成 0；
除以标准差（缩放），让整体方差变成 1。
结果：
这一层的输出分布被“归一化”成标准正态分布（平均为 0，方差为 1）。

第 3 步：加入两个可学习参数 γ（gamma）和 β（beta）

归一化之后，虽然分布变稳定了，但所有层的输出都变成了标准正态分布（太“死板”）。
模型可能需要“更灵活的”输出范围，比如某些层希望输出更大或更偏移。
所以：
我们给 BN 加两个参数，让模型自己去学：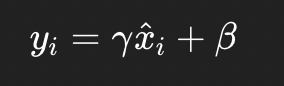

γ（gamma）控制“缩放”程度（相当于调整方差）；
β（beta）控制“平移”程度（相当于调整均值）。

它们都是可学习的参数，会随着训练自动更新。

5、全卷积网络（Fully Convolutional Network, FCN）

问题的提出

如果在128*128的 Imagenette 上使用cnn，会有两个问题
需要太多 stride=2 的卷积层 才能把 128×128 的特征图变成 1×1，这样模型会变得又深又慢。
只能处理固定大小的输入，如果训练时是 128×128，将来换成 224×224 就不行了。
代码：
def avg_pool(x): return x.mean((2,3))
它对最后两维（x, y 方向）求平均，从而把 bs x ch x h x w 变成 bs x ch。
PyTorch 里提供了一个更灵活的模块：
nn.AdaptiveAvgPool2d(1)
它可以自动把任何尺寸的特征图变成 1×1。

全卷积网络的结构

这样的网络一般是：
一系列卷积层（有些 stride=2）
最后接一个 Adaptive Average Pooling
再接一个 Flatten
最后接一个 Linear 层 输出分类结果。
代码示例：

def block(ni, nf): return ConvLayer(ni, nf, stride=2)
def get_model():
return nn.Sequential(
block(3, 16),
block(16, 32),
block(32, 64),
block(64, 128),
block(128, 256),
nn.AdaptiveAvgPool2d(1),
Flatten(),
nn.Linear(256, dls.c)
)

6、ResNet（残差网络）

背景：深层网络训练困难

在 ResNet 出现之前，研究者发现一个奇怪的现象：

网络层数越多，性能反而变差。

不是因为过拟合（overfitting），而是因为**训练误差（training error）**本身变高。
也就是说，SGD（随机梯度下降）根本训练不好更深的网络。

按理说，如果我们在一个 20 层网络上训练好了参数，再把它“扩展”成 56 层（后面加一些不做任何操作的层），那 56 层网络理论上至少不会比 20 层差。
但在实践中却发现 —— 优化算法找不到这么好的解。

核心思想：跳跃连接（Skip Connection）

ResNet 的核心在于一种结构叫 跳跃连接（skip connection）或 残差连接（residual connection）。
用公式表示就是：

也就是说，这个模块不直接学习“目标输出 ，而是学习“目标输出和输入的差值（残差）”。这就是 “Residual Network” 的由来。
为什么这样做能改善训练？因为在训练时，如果最优的映射其实是“恒等映射”（即输出等于输入），那么只要 F(x)=0 就能实现。
相比让网络直接学“恒等映射”，让它学“偏离恒等的差值”要容易得多。

ResBlock 的实现

class ResBlock(Module):
def __init__(self, ni, nf, stride=1):
self.convs = _conv_block(ni,nf,stride)
self.idconv = noop if ni==nf else ConvLayer(ni, nf, 1, act_cls=None)
self.pool = noop if stride==1 else nn.AvgPool2d(2, ceil_mode=True)
def forward(self, x):
return F.relu(self.convs(x) + self.idconv(self.pool(x)))

这里：
noop 表示“不做任何操作”（no operation）；
idconv 只在通道数不同时起作用；
pool 只在 stride≠1 时起作用；
ReLU 激活放在最后（整个 block 当成一个逻辑层）。
它做的事情就是：输入 x，经过两层卷积，再加回原始 x。
用 AvgPool2d(stride=2) 来让 x 的空间尺寸对齐；
用 1×1 卷积 改变通道数，使 x 能和输出相加。

ResNet 的改进：加入 “Stem” 层

ResNet 的前几层占据了大部分计算量，
因为图像在最开始分辨率很高（如 128×128），
每个卷积操作都需要处理非常多像素。

因此，ResNet 的第一部分（称为 Stem）
采用几层普通的卷积（ConvLayer）+ 最大池化（MaxPool）：

def _resnet_stem(*sizes):
return [
ConvLayer(sizes[i], sizes[i+1], 3, stride=2 if i==0 else 1)
for i in range(len(sizes)-1)
] + [nn.MaxPool2d(kernel_size=3, stride=2, padding=1)]

Stem 的作用：
先用几层简单的卷积快速“压缩”图像；
减少后续复杂 ResNet Block 的计算压力；
前面计算多、参数少；后面计算少、参数多。

例如：
第一层卷积：3 输入通道 → 32 输出通道，参数约 864；
最后一层卷积：256 输入通道 → 512 输出通道，参数超过 117 万。
所以前几层是 计算密集型（compute-heavy），
而后几层是 参数密集型（parameter-heavy）。

完整的现代 ResNet 架构

在 fastai 的实现中，ResNet 包含四组残差块：
第 1 组：64 通道
第 2 组：128 通道
第 3 组：256 通道
第 4 组：512 通道

除了第一组外，每组的第一个 block stride=2 用来下采样。

class ResNet(nn.Sequential):
def __init__(self, n_out, layers, expansion=1):
stem = _resnet_stem(3,32,32,64)
self.block_szs = [64,64,128,256,512]
for i in range(1,5): self.block_szs[i] *= expansion
blocks = [self._make_layer(*o) for o in enumerate(layers)]
super().__init__(*stem, *blocks,
nn.AdaptiveAvgPool2d(1), Flatten(),
nn.Linear(self.block_szs[-1], n_out))

_make_layer 的功能：
根据 layers=[2,2,2,2] 等参数，
生成对应数量的 ResBlock，每组之间控制 stride。
rn = ResNet(dls.c, [2,2,2,2]) # 相当于 ResNet-18

让网络更深：Bottleneck 层

为了在不增加太多计算量的情况下加深网络，
ResNet-50 及更深版本（如 ResNet-101、152）引入了 瓶颈层（bottleneck layer）。
它不再堆叠两个 3×3 卷积，而是：
1×1 → 3×3 → 1×1
结构示意：
输入通道 → 降维(1×1) → 卷积(3×3) → 升维(1×1)

为什么这样更高效？
1×1 卷积非常快；
中间层用较少通道数进行 3×3 卷积；
最后再恢复通道数（expand back）。
→ 参数更少，速度更快，还能增加特征数（通常 ×4）。

代码：

def _conv_block(ni,nf,stride):
return nn.Sequential(
ConvLayer(ni, nf//4, 1),
ConvLayer(nf//4, nf//4, stride=stride),
ConvLayer(nf//4, nf, 1, act_cls=None, norm_type=NormType.BatchZero))

ResNet-50 的定义与训练

ResNet-50 的四个阶段的 block 数量为 [3,4,6,3]。

rn = ResNet(dls.c, [3,4,6,3], 4)  # 4 表示 bottleneck 扩展倍数

换更大的图片：

dls = get_data(URLs.IMAGENETTE_320, presize=320, resize=224)

因为网络是 全卷积结构（Fully Convolutional），
所以输入尺寸可以随意变化，模型仍能正常工作。