相机内外参2D-3D转换 - 实践

相机成像原理反向应用 | 如何运用相机内外参，将2D的照片$(u,v)$转换回3D世界坐标$(x,y,z)$

已知当前 $m$ 个帧 $f_i^m$ 的深度图 ${\mathbf{D}}_i^m$和相机内外参数${\mathbf{E}}_i^m$、${\mathbf{K}}_i^m$，借助深度重投影重建 3D 点图${\mathcal{P}}_i^m$：

$${\mathcal{P}}_i^m=D_i^m\cdot K_i^{-1}[u|v|1{]}^{\top }\cdot E_i^{-1}$$

符号	类型	维度 / 取值范围	核心物理意义
${\mathcal{P}}_i^m$	输出	3D 向量（x, y, z）	2D 像素（u,v）在3D 世界坐标系中的坐标（单位：米），是最终需要的 3D 空间位置
$D_i^m$	输入	标量（>0）	第 $i$个候选帧中，像素（u,v）对应的深度值（即像素到相机的直线距离，单位：米）
$K_i^m$	输入	3×3 矩阵	相机 内参矩阵（Intrinsic Matrix），描述相机光学特性（焦距、像素尺寸等）
$E_i^m$	输入	4×4 矩阵	相机 外参矩阵（Extrinsic Matrix），描述相机在 3D 世界坐标系中的位置和姿态
$[u|v|1{]}^{\top }$	输入	3D向量	2D 像素的齐次坐标（Homogeneous Coordinate），(u,v) 是像素在图像中的行列坐标（单位：像素）
$K_i^{-1}$	中间变量	3×3 矩阵	相机内参矩阵的逆矩阵，用于将 “像素坐标” 转化为 “相机坐标系下的射线方向”
$E_i^{-1}$	中间变量	4×4 矩阵	相机外参矩阵的逆矩阵，用于将 “相机坐标系下的 3D 点” 转化为 “世界坐标系下的 3D 点”

该公式的计算过程是 “分步可逆” 的，对应相机成像的逆过程（相机成像：3D 世界→2D 图像；公式计算：2D 图像→3D 世界），具体拆解为 4 个关键步骤：

Stage1：2D 像素坐标→齐次坐标：$[u\Vert v\Vert 1{]}^{\top }$

增加 “1” 作为第三维，将离散的像素行列坐标$(u,v)$转化为连续的数学向量，方便后续利用矩阵乘法实现平移、旋转等变换。

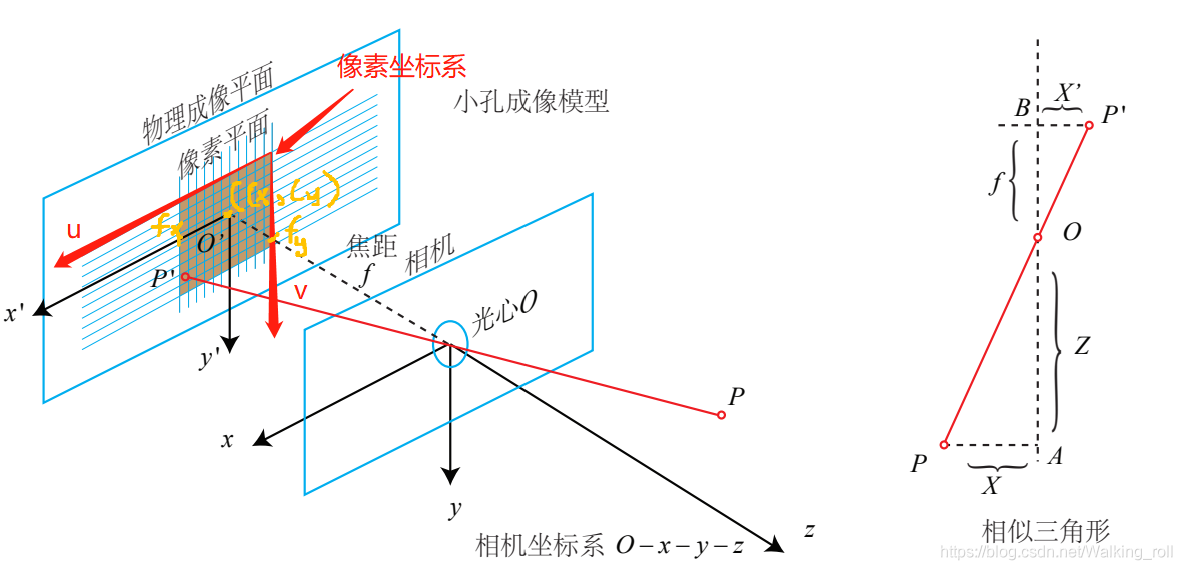
Stage2：齐次坐标→相机坐标系下的射线方向：$K_i^{-1}\cdot [u\Vert v\Vert 1{]}^{\top }$

通过相机内参的逆矩阵，消除“相机光学畸变”和“像素尺寸”的影响，得到“该像素在相机坐标系下的射线方向”。

$$K_i^m=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]，\because K\cdot 射线=齐次坐标\therefore K^{-1}\cdot 齐次坐标=射线$$

$$\begin{array}{cccccccccccccccccccc}3,3& & & & & & & & & 3,1& & & & & & & & & & 3,1\end{array}$$

Stage3：射线方向→相机坐标系下的3D点：$D_i^m\cdot K_i^{-1}\cdot [u\Vert v\Vert 1{]}^{\top }$

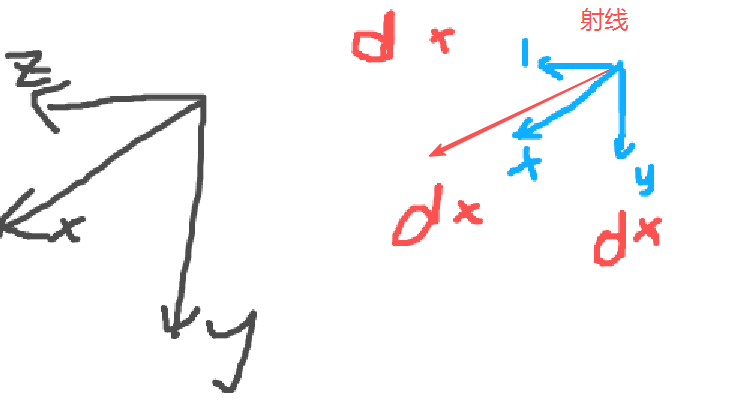
Stage4：相机坐标系→世界坐标系：$D_i^m\cdot K_i^{-1}\cdot [u\Vert v\Vert 1{]}^{\top }\cdot E_i^{-1}$

描述相机在 3D 世界坐标系中的 “位置（平移）” 和 “姿态（旋转）”，标准形式为 “4×4 齐次矩阵”（前 3×3 为旋转矩阵$R$，后 3×1 为平移向量$t$，描述相机在世界中的位置）：

$$E_i^m=\left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]$$

原理：在使用外参的时候，先把世界坐标系加上1作为第四维度，之后与外参运算

$$(x,y,z,1)\cdot \left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]=四维齐次坐标$$

$$\begin{array}{cccccccc}1,4& & & 4,4& & & & 1,4\end{array}$$