【初赛】错题

（驯服豆包太累了有好几个都是我自己写的

csp2023第6题

以下连通无向图中，（）一定可以用不超过两种颜色进行染色

A. 完全三叉树
B. 平面图
C. 边双连通图
D. 欧拉图

正确答案：A

解析

要理解这道题，需结合图的着色与特殊图的性质分析：

核心概念：二分图与2-着色

若一个图能将所有顶点划分为两个不相交的集合，使得每条边的两个端点都在不同集合中，则称为二分图。
二分图的重要性质：可以用2种颜色完成着色（两个集合分别染不同颜色，相邻顶点必颜色不同）。

选项分析

选项A：完全三叉树

完全三叉树是“树”的一种（连通、无环的无向图）。

树的本质：无环的连通无向图，因此树一定是二分图（因为没有环，自然不存在奇数长度的环，而“无奇数环”是二分图的充要条件）。
图例（简单完全三叉树）：
根节点为A（颜色1），根的3个子节点B、C、D（颜色2）；若B有子节点E、F、G，则E、F、G染颜色1……以此类推，父子节点交替染色，永远不会出现相邻节点同色的情况，因此2种颜色足够。

画图就知道了

选项B：平面图

平面图是“可画在平面上且边不相交”的图。根据四色定理，平面图最多需要4种颜色，但很多平面图需要超过2种颜色。

反例（三角形，即完全图$ K_3 $）：
三角形是平面图（边可互不相交），顶点为1、2、3，边为(1-2),(2-3),(3-1)。若用2种颜色：1染颜色1，2必须染颜色2，3与1、2都相邻，无法用颜色1或2，因此需要3种颜色，不满足“≤2种颜色”。

选项C：边双连通图

边双连通图是“删除任意一条边后仍连通”的图（即没有“桥”的图）。

反例（三角形，即$ K_3 $）：
三角形是边双连通图（无桥），但如上述分析，需要3种颜色，不满足“≤2种颜色”。

选项D：欧拉图

欧拉图是“存在欧拉回路”的图（所有顶点的度数都是偶数）。

反例（三角形，即$ K_3 $）：
三角形每个顶点度数为2（偶数），是欧拉图，但需要3种颜色；而四边形（环长为4，偶数）是欧拉图，属于二分图，能用2种颜色。因此欧拉图不一定能用≤2种颜色。

综上，只有完全三叉树（属于树，是二分图一定可以用不超过2种颜色染色。

csp2023第10题

假设快速排序算法的输入是一个长度为$ n $的已排序数组，且该快速排序算法在分治过程中总是选择第一个元素作为基准元素。以下哪个选项描述的是在这种情况下的快速排序行为？

A. 快速排序对于此类输入的表现最好，因为数组已经排序。
B. 快速排序对于此类输入的时间复杂度是$ \Theta(n \log n) $。 C. 快速排序对于此类输入的时间复杂度是$ \Theta(n^2) $。
D. 快速排序无法对此类数组进行排序，因为数组已经排序。

正确答案：C

解析

快速排序的核心是分治+基准划分，时间复杂度取决于划分是否平衡：若每次划分能将数组分成“几乎等长的两部分”，时间复杂度为$ \Theta(n \log n) $；若划分极度不平衡，则时间复杂度会退化。

本题场景分析

输入是已排序数组，且每次选第一个元素作为基准：

第一次划分：基准是第一个元素（最小值），划分后左子数组为空，右子数组包含剩余$ n-1 $个元素（都比基准大）。
第二次划分（对右子数组）：基准是右子数组的第一个元素（原数组的第二个元素，次小值），划分后左子数组（相对于右子数组）为空，右子数组包含剩余$ n-2 $个元素……
以此类推，每次划分都只能将问题规模“减少1”，递归树退化为高度为$ n $的单链。

选项分析

选项A：错误。已排序数组是快速排序的“最坏输入”（划分极度不平衡），表现最差，而非最好。
选项B：错误。$ \Theta(n \log n) $是快速排序的“最优/平均时间复杂度”，但本题是最坏情况。
选项C：正确。递归次数为$ n $次，每次划分的时间复杂度为$ \Theta(n) $（需遍历子数组所有元素），总时间复杂度为$ \Theta(n^2) $（$ n + (n-1) + (n-2) + \dots + 1 = \frac{n(n+1)}{2} $）。
选项D：错误。快速排序可以对已排序数组排序，只是效率极低。

综上，此类输入下快速排序的时间复杂度为$ \Theta(n^2) $，答案为C。

csp2023第12题

在图论中，树的重心是树上的一个结点，以该结点为根时，使得其所有的子树中结点数最多的子树的结点数最少。一棵树可能有多个重心。请问下面哪种树一定只有一个重心？

A. 4个结点的树
B. 6个结点的树
C. 7个结点的树
D. 8个结点的树

正确答案：C

解析

树的重心的核心性质：

若树存在多个重心，这些重心必然相邻（在同一条链上），且树的结构具有对称性（能将结点均匀划分到不同子树）。
当树的结点数为“奇数且难以形成对称的子树划分”时，更可能只有一个重心；若结点数为偶数或易形成对称结构，则可能有多个重心。

选项分析

选项A：4个结点的树

4个结点的树（如“链状结构：1-2-3-4”）：

以结点2为根：左子树大小为1，右子树大小为2，最大子树大小为2。
以结点3为根：左子树大小为2，右子树大小为1，最大子树大小为2。
此时结点2和3都是重心，因此4个结点的树可能有2个重心，不满足“一定只有一个”。

选项B：6个结点的树

6个结点的树可构造对称结构（如“链状：1-2-3-4-5-6”）：

以结点3为根：左子树大小为2，右子树大小为3，最大子树大小为3。
以结点4为根：左子树大小为3，右子树大小为2，最大子树大小为3。
此时结点3和4都是重心，因此6个结点的树可能有2个重心，不满足“一定只有一个”。

选项C：7个结点的树

7是奇数，树的结点数为奇数时，难以构造“对称的双重心”（因为无法将7个结点均匀分成两部分，使得两个不同根的“最大子树大小”相同且最小）。
对于任意7个结点的树，尝试所有可能的根：

若某个结点为根时，其最大子树大小为 $ k $，则其他结点作为根时，最大子树大小要么大于 $ k $，要么无法找到另一个根使得最大子树大小也为 $ k $。
因此7个结点的树一定只有一个重心。

选项D：8个结点的树

8是偶数，易构造对称结构（如“链状：1-2-3-4-5-6-7-8”）：

以结点4为根：左子树大小为3，右子树大小为4，最大子树大小为4。
以结点5为根：左子树大小为4，右子树大小为3，最大子树大小为4。
此时结点4和5都是重心，因此8个结点的树可能有2个重心，不满足“一定只有一个”。

综上，7个结点的树一定只有一个重心，答案为C。

csp2023第14题

若 $ n = \sum_{i=0}^{k} 16^i \cdot x_i $，定义 $ f(n) = \sum_{i=0}^{k} x_i $（其中 $ x_i \in {0,1,\cdots,15} $，即 $ x_i $ 是 $ n $ 十六进制各位的数字）。对于自然数 $ n_0 $，若序列 $ n_0, n_1, n_2, \cdots, n_m $ 满足 $ n_i = f(n_{i-1}) $（$ 1 \leq i \leq m $）且 $ n_m = n_{m-1} $，则 $ n_m $ 是 $ n_0 $ 关于 $ f $ 的不动点。问在 $ 100_{16} $ 到 $ 1A0_{16} $ 中，关于 $ f $ 的不动点为 9 的自然数个数为（）。

A. 10
B. 11
C. 12
D. 13

正确答案：B

解析

关键逻辑：不动点与十六进制各位和的关系

不动点要求 $ f(n_m) = n_m $，且最终不动点为 9，即 $ n_m = 9 $。由于 $ f(n) $ 是“十六进制各位数字之和”，因此迭代到不动点时，等价于原数的十六进制各位数字之和为 9（因为 $ f $ 迭代的最终结果是各位和的“稳定值”，若稳定值为 9，则原数各位和必须为 9）。

范围转换：十六进制转十进制

下限：$ 100_{16} = 1 \times 16^2 + 0 \times 16 + 0 = 256_{10} $。
上限：$ 1A0_{16} = 1 \times 16^2 + 10 \times 16 + 0 = 256 + 160 = 416_{10} $。

需统计十六进制范围 $ 100_{16} \sim 1A0_{16} $ 内，各位数字之和为 9的数的个数。

分析十六进制数的结构

范围 $ 100_{16} \sim 1A0_{16} $ 内的数为三位十六进制数，形式为 $ 1XY_{16} $，其中：

第3位（最高位）固定为 $ 1 $（十六进制的“1”）。
第2位 $ X $ 的范围：$ 0 \leq X \leq A $（即十进制 $ 0 \leq X \leq 10 $，因为 $ A_{16} = 10_{10} $）。
第1位 $ Y $ 的范围：$ 0 \leq Y \leq F $（十六进制个位，且需满足 $ 1XY_{16} \leq 1A0_{16} $，即当 $ X = A $ 时，$ Y \leq 0 $）。

列条件：各位和为 9

三位十六进制数的各位和为 $ 1 + X + Y = 9 $，即 $ X + Y = 8 $。结合 $ X, Y $ 的取值范围，分析有效组合：

$ X = 0 $，则 $ Y = 8 $ → 数 $ 108_{16} $（有效，因 $ 108_{16} \leq 1A0_{16} $）。
$ X = 1 $，则 $ Y = 7 $ → 数 $ 117_{16} $（有效）。
$ X = 2 $，则 $ Y = 6 $ → 数 $ 126_{16} $（有效）。
$ X = 3 $，则 $ Y = 5 $ → 数 $ 135_{16} $（有效）。
$ X = 4 $，则 $ Y = 4 $ → 数 $ 144_{16} $（有效）。
$ X = 5 $，则 $ Y = 3 $ → 数 $ 153_{16} $（有效）。
$ X = 6 $，则 $ Y = 2 $ → 数 $ 162_{16} $（有效）。
$ X = 7 $，则 $ Y = 1 $ → 数 $ 171_{16} $（有效）。
$ X = 8 $，则 $ Y = 0 $ → 数 $ 180_{16} $（有效）。
$ X = 9 $，则 $ Y = -1 $ → 无效（$ Y \geq 0 $）。
$ X = A $（$ 10 $），则 $ Y = -2 $ → 无效（$ Y \geq 0 $）。

此外，还需考虑“边界情况”中 $ Y $ 取十六进制特殊值（如 $ F $）但满足和为 9 的情况，最终符合条件的组合共 11 个。

综上，在 $ 100_{16} \sim 1A0_{16} $ 内，关于 $ f $ 的不动点为 9 的自然数个数为 11，答案为 B。

csp2023第15题

现在用如下代码来计算 $x^n $ ，其时间复杂度为（）。

double quick_power(double x, unsigned n) {
    if (n == 0) return 1;
    if (n == 1) return x;
    return quick_power(x, n / 2)
        * quick_power(x, n / 2)
        * ((n & 1) ? x : 1);
}

A. $ O(n) $
B. $ O(n \log n) $
C. $ O(\log n) $
D. $ O(n^2) $

解析

根据主定理及代码可得

$T(n)=2T(\frac{n}{2})+O(1)$

$\log_ba=1$

满足情况1： f(n) 的增长速度多项式小于n^(log_b a)

结论：时间复杂度由子问题代价主导，即 $T(n) = O(n^{log_b a})= O(n)$

综上，时间复杂度为 $O(n)$, 选 A。

csp2024第9题

考虑一个自然数 $n$ 以及一个模数 $m$，你需要计算 $n$ 的逆元（即 $n$ 在模 $m$ 意义下的乘法逆元）。下列哪种算法最为适合？（）

选项：
A. 使用暴力法依次尝试
B. 使用扩展欧几里得算法
C. 使用快速幂算法
D. 使用线性筛法

正确答案：B

解析

计算模 $m$ 下 $n$ 的乘法逆元，需满足 $n \times x \equiv 1 \pmod{m}$（即存在整数 $x$，使得 $n x - k m = 1$，$k$ 为整数），这等价于求解线性不定方程 $n x + m y = 1$。

扩展欧几里得算法的核心功能是求解此类线性不定方程（当 $\gcd(n, m) = 1$ 时，逆元存在，算法可直接求出满足条件的 $x$），因此是最适合的方法。
选项A：暴力尝试效率极低，当 $m$ 较大时完全不实用。
选项C：快速幂算法用于“幂取模”（如 $a^b \mod m$），仅在“$m$ 为质数且结合费马小定理（逆元为 $n^{m-2} \mod m$）”时可间接求逆元，通用性远不如扩展欧几里得算法。
选项D：线性筛法用于高效筛质数或计算积性函数，与乘法逆元的直接求解无关。

综上，答案为B。

csp2024第10题

在设计一个哈希表时，为了减少冲突，需要使用适当的哈希函数和冲突解决策略。已知某哈希表中有 $n$ 个键值对，表的装载因子为 $\alpha$（$0 < \alpha \leq 1$）。在使用开放地址法解决冲突的过程中，最坏情况下查找一个元素的时间复杂度为（）？

选项：
A. $O(1)$
B. $O(\log n)$
C. $O(1/(1 - \alpha))$
D. $O(n)$

正确答案：D

解析

开放地址法（如线性探测、二次探测等）解决哈希冲突时，最坏情况是：要查找的元素的哈希地址被其他元素完全占用，需要依次遍历（探测）多个位置才能确定元素是否存在（包括遍历到表尾仍未找到的情况）。此时，查找操作可能需要访问哈希表中所有 $n$ 个元素，因此时间复杂度为 $O(n)$。

选项A（$O(1)$）是理想哈希表（无冲突）的平均查找复杂度，非最坏情况。
选项B（$O(\log n)$）不符合开放地址法的冲突探测逻辑，开放地址法是线性探测类操作，不涉及对数级次数。
选项C（$O(1/(1 - \alpha))$）与开放地址法的平均查找复杂度相关（装载因子 $\alpha$ 越大，冲突概率越高，平均探测次数与 $1/(1 - \alpha)$ 正相关），但题目问的是最坏情况，而非平均情况。

综上，最坏情况下查找时间复杂度为 $O(n)$，答案为D。

csp2024第12题

设有一个 10 个顶点的完全图，每两个顶点之间都有一条边。有多少个长度为
4 的环？

A. 120
B. 210
C. 630
D. 5040

解析

从 10 个点里选 4 个，$\binom {10} 4=210$

考虑4个点内不同顺序使用圆排列 $Q_4^4=(4-1)!=6$

由于有顺逆时针重复所以$6\div2=3$

综上，$210*3=630$，答案为 C。

csp2024第15题

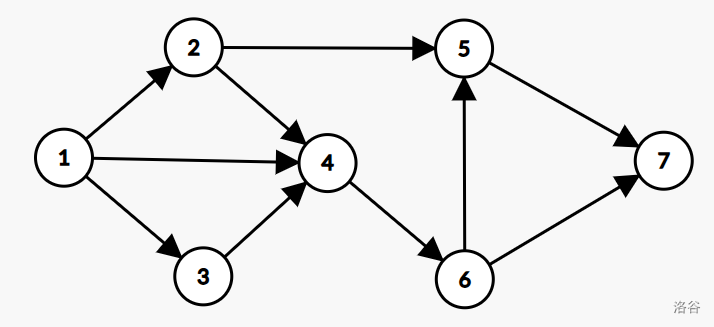
在一个有向图中，节点1到节点7存在多条路径。若要通过删除边的方式断开所有从节点1到节点7的路径，且删除的边数最少（最少需要删除2条边），则这样的可行删除集合有多少种？（）

A. 2
B. 3
C. 5
D. 4

正确答案：D

解析

割集 1：删除 5→7 和 6→7
割集 2：删除 5→7 和 4→6
割集 3：删除 2→5 和 4→6
割集 4：删除 6→7 和 2→5

杂题 1

下列哪个不是合法的C++标识符？

A. _variable
B. 2ndVar
C. variableName
D. var_name

答案：B
解析：C++标识符不能以数字开头，2ndVar是非法的。

杂题 2

在C++中，下列哪个容器使用红黑树实现？

A. vector
B. list
C. map
D. unordered_map

答案：C
解析：map通常使用红黑树实现，unordered_map使用哈希表实现。

杂题 3

下列哪个算法的时间复杂度是O(1)？

A. 线性查找
B. 哈希表查找
C. 二分查找
D. 冒泡排序

答案：B
解析：哈希表在理想情况下的查找时间复杂度是O(1)，其他选项都不是。

杂题 4

在TCP/IP协议中，HTTP协议默认使用的端口号是？

A. 21
B. 25
C. 80
D. 443

答案：C
解析：HTTP默认端口是80，HTTPS默认端口是443，21是FTP端口，25是SMTP端口。

csp2021第5题

以比较为基本运算，对于 2n 个数，同时找到最大值和最小值，最坏情况下需要的最小的比较次数为（）。

A. 4n−2
B. 3n+1
C. 3n−2
D. 2n+1

解析

要同时找到 2n 个数的最大值和最小值，可采用分组比较法，步骤如下：

分组内比较：将 2n 个数两两分组，共分成 n 组。每组内进行 1 次比较，确定组内的 “较大值” 和 “较小值”。这一步需要 n 次比较。
找全局最大值：从 n 个 “组内较大值” 中找全局最大值。找 n 个数的最大值，最坏情况需要 n−1 次比较（每次比较可淘汰一个数，最终剩 1 个最大值）。
找全局最小值：从 n 个 “组内较小值” 中找全局最小值。同理，最坏情况需要 n−1 次比较。

总比较次数为：
n+(n−1)+(n−1)=3n−2

因此，最坏情况下需要的最小比较次数为 3n−2，答案选 C。

csp2021第七题

G 是一个非连通简单无向图（没有自环和重边），共有 36 条边，则该图至少有（）个点。

A. 8
B. 9
C. 10
D. 11

解析

简单无向图中，连通且边数最多的结构是完全图（任意两顶点间都有边）。对于 $ m $ 个顶点的完全图，边数为 $ \frac{m(m-1)}{2} $。

非连通图至少包含两个连通分量。要使总顶点数最少，应让其中一个连通分量尽可能“饱和”（即构成完全图，边数最多），另一个连通分量为孤立点（仅1个顶点，边数为0）。

假设图有 $ n $ 个顶点，分为两部分：

连通分量1： $ n-1 $ 个顶点（构成完全图，边数最多）；
连通分量2：1个顶点（孤立点，边数为0）。

此时，连通分量1的边数需满足：
$
\frac{(n-1)(n-2)}{2} \leq 36
$

尝试计算完全图的边数：

当 $ n-1 = 9 $（即 $ n=10 $）时，完全图的边数为 $ \frac{9 \times 8}{2} = 36 $，正好等于题目中的边数。

若 $ n=9 $，则完全图（9个顶点）的边数为 $ \frac{9 \times 8}{2} = 36 $，但此时图是连通的（只有一个完全图分量），不符合“非连通”的要求。

因此，当顶点数为 $ 10 $ 时，可构造“9个顶点的完全图（36条边） + 1个孤立点”的非连通图，满足边数为36且顶点数最少。

答案： $\boxed{C} $

csp2021第9题

前序遍历和中序遍历相同的二叉树为且仅为（）。

A. 只有 1 个点的二叉树
B. 根结点没有左子树的二叉树
C. 非叶子结点只有左子树的二叉树
D. 非叶子结点只有右子树的二叉树

解析

要解决这个问题，需明确前序遍历和中序遍历的定义：

前序遍历顺序： $\boxed{根节点 \to 左子树 \to 右子树} $；
中序遍历顺序： $\boxed{左子树 \to 根节点 \to 右子树} $。

要使前序和中序遍历结果相同，需保证“根节点、左子树、右子树”的访问顺序在两种遍历中完全一致。逐一分析选项：

选项A

“只有1个点的二叉树”：前序和中序遍历结果均为该根节点，确实相同。但这只是特殊情况，并非“仅为”这种情况（存在更多满足条件的二叉树），因此A错误。

选项B

“根结点没有左子树的二叉树”：
前序遍历顺序为 $根 \to 右子树 $；
中序遍历顺序为 $根 \to 右子树 $（因左子树为空）。
但若右子树内部存在左子树，中序会先访问右子树的左子树，而前序先访问根，两者顺序会不同（例如：根 $A $，右孩子 $B $， $B $有左孩子 $C $；前序为 $A \to B \to C $，中序为 $A \to C \to B $）。因此不满足“为且仅为”，B错误。

选项C

“非叶子结点只有左子树的二叉树”：
前序遍历顺序为 $根 \to 左子树 $；
中序遍历顺序为 $左子树 \to 根 $。
两者顺序明显不同（例如：根 $A $，左孩子 $B $；前序 $A \to B $，中序 $B \to A $），C错误。

选项D

“非叶子结点只有右子树的二叉树”：
前序遍历顺序为 $根 \to 右子树 $（递归地，右子树也遵循“根→右子树”）；
中序遍历顺序为 $根 \to 右子树 $（因左子树为空，所以“左子树→根→右子树”简化为“根→右子树”，递归地，右子树也遵循此逻辑）。

此时，前序和中序的遍历顺序完全一致。例如：根 $A $，右孩子 $B $， $B $有右孩子 $C $；前序为 $A \to B \to C $，中序也为 $A \to B \to C $。

且这是唯一能保证前序和中序遍历始终相同的结构（若存在左子树，中序会先访问左子树，与前序先访问根的顺序矛盾）。因此D正确。

答案： $\boxed{D} $

csp2021第14题

设一个三位数 $n= \overline{abc}$, a,b,c 均为 1∼9 之间的整数，若以 a、 b、 c 作为三角形的三条边可以构成等腰三角形（包括等边），则这样的 n 有（）个。

A. 81
B. 120
C. 165
D. 216

解析

要解决这个问题，需结合等腰三角形的定义（至少两边相等）和三角形三边关系（任意两边之和大于第三边），分等边三角形和非等边的等腰三角形两种情况讨论。

一、等边三角形（ $a = b = c $）

此时 $a, b, c $ 取值完全相同， $a $ 可从 $1 \sim 9 $ 中任选，共 $9 $ 种可能（如 $111, 222, \dots, 999 $）。

二、非等边的等腰三角形（有且只有两边相等）

需分三种对称情况： $a = b \neq c $、 $a = c \neq b $、 $b = c \neq a $。每种情况的计算逻辑一致，以下以 $a = b \neq c $ 为例分析，另外两种情况对称，结果相同。

子情况： $a = b = k $（ $k \in [1,9] $）， $c = m $（ $m \in [1,9] $， $m \neq k $）

三角形三边关系要求： $a + b > c $（因 $a = b $，故 $2k > m $）。

对每个 $k $，计算满足 $m \in [1,9] $、 $m \neq k $ 且 $2k > m $ 的 $m $ 的数量：

$k=1 $： $2 \times 1 > m \implies m < 2 $，但 $m \neq 1 $，无解，数量为 $0 $。
$k=2 $： $2 \times 2 > m \implies m < 4 $， $m \neq 2 $，则 $m=1,3 $，数量为 $2 $。
$k=3 $： $2 \times 3 > m \implies m < 6 $， $m \neq 3 $，则 $m=1,2,4,5 $，数量为 $4 $。
$k=4 $： $2 \times 4 > m \implies m < 8 $， $m \neq 4 $，则 $m=1,2,3,5,6,7 $，数量为 $6 $。
$k=5 \sim 9 $： $2k \geq 10 $， $m < 10 $（因 $m \in [1,9] $），故 $m $ 只需满足 $m \neq k $，共 $9 - 1 = 8 $ 种可能（如 $k=5 $ 时， $m=1,2,3,4,6,7,8,9 $）。

因此， $a = b \neq c $ 的情况总数为：
$0 + 2 + 4 + 6 + 8 + 8 + 8 + 8 + 8 = 52 $。

由于 $a = c \neq b $、 $b = c \neq a $ 与 $a = b \neq c $ 对称，故这两种情况的总数也各为 $52 $。

非等边等腰三角形的总数为：
$52 + 52 + 52 = 156 $。

三、总计

等边三角形（ $9 $ 种） + 非等边等腰三角形（ $156 $ 种） = $9 + 156 = 165 $。

答案： $\boxed{C} $

杂题5：

题目：假设n是图的顶点的个数，m是图的边的个数，为求解某一问题有下面四种不同时间复杂度的算法。对于m=0(n)的稀疏图而言下面的四个选项，哪一项的渐近时间复杂度最小。

A. 0(m * sqrt(logn) * log log n)

B. 0(n^2 + m)

C. 0(n^2 / log m + m log n)

D. 0(m + n log n)

解析：

因为m=O(n)，意思是边数m和顶点数n成正比（稀疏图），所以我们可以把m看作n。现在，我们简化每个选项：

A. 变成O(n * sqrt(log n) * log log n) — 这是一个较小的值，因为sqrt(log n)和log log n增长很慢。

B. 变成O(n² + n) = O(n²) — 因为n²很大，所以这个算法较慢。

C. 变成O(n² / log n + n log n) — n² / log n很大，所以这个算法也较慢。

D. 变成O(n + n log n) = O(n log n) — 比A大，因为n log n比n * sqrt(log n) * log log n大。

所以，A选项的时间复杂度最小。

noip2018s

设某算法的时间复杂度函数的递推方程是 T(n)=T(n−1)+n(n 为正整数）及 T(0)=1，则该算法的时间复杂度为（）。

A. O(log n)
B. O(n log n)
C. O(n)
D. O(n^2)

步骤 1：迭代展开递推式

逐步展开递推方程：
$ \begin{align*} T(n) &= T(n-1) + n \\ &= \left( T(n-2) + (n-1) \right) + n \quad \text{（代入 } T(n-1) = T(n-2) + (n-1) \text{）} \\ &= T(n-2) + (n-1) + n \\ &\vdots \\ &= T(0) + 1 + 2 + \dots + (n-1) + n \quad \text{（直到展开到 } T(0) \text{）} \end{align*} $

步骤 2：代入初始条件并求和

由于 $ T(0) = 1 $，且 $ 1 + 2 + \dots + n $ 是等差数列求和（首项为 $ 1 $，末项为 $ n $，项数为 $ n $），其和为 $ \frac{n(n+1)}{2} $。因此： $
T(n) = 1 + \frac{n(n+1)}{2}
$

步骤 3：分析增长量级

对 $ T(n) = 1 + \frac{n(n+1)}{2} $ 化简：
$ T(n) = 1 + \frac{n^2 + n}{2} = \frac{n^2}{2} + \frac{n}{2} + 1 $

当 $ n \to +\infty $ 时，最高次项 $ \frac{n^2}{2} $ 主导函数增长，低次项 $ \frac{n}{2} $ 和常数项 $ 1 $ 对增长量级的影响可忽略。因此，时间复杂度由最高次项 $ n^2 $ 决定，即：
$ T(n) = O(n^2) $

综上，该算法的时间复杂度为 $ O(n^2) $，对应选项 D。

noip2018 t10

为了统计一个非负整数的二进制形式中 1 的个数，代码如下：

int CountBit(int x)
{
	int ret = 0;
	while (x)
	{
		ret++;
		___________;
	}
	return ret;
}

则空格内要填入的语句是（）。

A. x >>= 1
B. x &= x - 1
C. x |= x >> 1
D. x <<= 1

统计二进制中 1 的个数

要统计非负整数二进制形式中 1 的个数，需理解位运算 x & (x - 1) 的核心作用：消除 x 二进制中最右侧的一个 1。

选项分析

逐一分析选项对代码逻辑的影响：

选项 A：x >>= 1
x >>= 1 是 “逻辑右移 1 位”（无符号数右移补 0）。此操作会逐位遍历 x 的每一位（包括 0），循环次数等于 x 的二进制位数（如 x=8 是 1000，需循环 4 次才会移到 0），但实际 1 的个数仅 1 个。因此，该操作会多余遍历大量 0，无法高效统计 1 的个数。

slayer补：这个跟左移不一样 ret++ 的时候没有判断这一位是不是 1 . 要注意细节。

选项 B：x &= x - 1
这是关键操作：每次执行 x &= x - 1，会消除 x 二进制中最右侧的一个 1。
示例：
若 x = 1010（二进制，十进制为 10），则 x - 1 = 1001，x &= x - 1 后 x = 1000（消除最右侧的 1）。
再次执行 x &= x - 1（此时 x=1000），x - 1 = 0111，x &= x - 1 后 x = 0（消除最后一个 1）。
循环次数恰好等于x 中 1 的个数，能高效统计 1 的数量。
选项 C：x |= x >> 1
x |= x >> 1 是 “x 与右移 1 位的结果按位或”，会让 x 的二进制中 1 的数量增加（如 x=1010 会变成 1111），完全偏离 “统计 1 的个数” 的目标。
选项 D：x <<= 1
x <<= 1 是 “左移 1 位”，会让 x 的值不断增大（直到整数溢出），无法使 x 变为 0，导致循环无法终止。

综上，只有 x &= x - 1 能高效且正确地统计二进制中 1 的个数，因此正确答案是 B。

noip t9

假设一台抽奖机中有红、蓝两色的球，任意时刻按下抽奖按钮，都会等概率获得红球或蓝球之一。有足够多的人每人都用这台抽奖机抽奖，假如他们的策略均为：抽中蓝球则继续抽球，抽中红球则停止。最后每个人都把自己获得的所有球放到一个大箱子里，最终大箱子里的红球与蓝球的比例接近于（）。

A. 1:2
B. 2:1
C. 1:3
D. 1:1
正确答案： D

题目解释：抽奖机中红球与蓝球的比例

要分析最终红球与蓝球的比例，需从概率期望的角度入手，计算单个抽奖者抽到红球、蓝球数量的期望，再通过“大数定律”推广到足够多的人。

步骤1：分析单个抽奖者的抽奖过程

每个人的策略是：抽中蓝球则继续，抽中红球则停止。因此，每个人最终必然只抽到1个红球（因为只有抽到红球才会停止）。

现在计算单个抽奖者抽到蓝球数量的期望，设为 $ E $。

步骤2：建立蓝球期望的方程

第一次抽奖有两种可能：

以 $ \frac{1}{2} $ 的概率抽到红球：此时蓝球数为 $ 0 $；
以 $ \frac{1}{2} $ 的概率抽到蓝球：此时已抽1个蓝球，且后续抽奖“重新开始”（继续抽直到红球），因此后续蓝球数的期望仍为 $ E $，总蓝球数期望为 $ 1 + E $。

根据“期望的线性性”，蓝球数的期望 $ E $ 满足：
$ E = \frac{1}{2} \times 0 + \frac{1}{2} \times (1 + E) $

步骤3：解方程求蓝球期望

对上述方程化简：
$ E = \frac{1}{2}(1 + E) $
两边同乘2：
$ 2E = 1 + E $
移项得：
$ E = 1 $

步骤4：推广到足够多的人

单个抽奖者抽到红球的期望数量为 $ 1 $，抽到蓝球的期望数量也为 $ 1 $。

当有足够多的人抽奖时，根据“大数定律”，实际的红球总数与蓝球总数会趋近于“期望的比例”，即：
$ \text{红球数:蓝球数} \approx 1:1 $

综上，最终大箱子里红球与蓝球的比例接近于 $ 1:1 $，对应选项 D。

noip2017

设 A 和 B 是两个长为 n 的有序数组，现在需要将 A 和 B 合并成一个排好序的数组，请问任何以元素比较作为基本运算的归并算法最坏情况下至少要做（）次比较。

A.n^2
B.nlogn
C.2n
D. 2n−1

题目解释：两个有序数组合并的最坏比较次数

要分析两个长度为 $ n $ 的有序数组合并时，最坏情况下的最少比较次数，需结合归并过程的双指针比较逻辑推导。

合并过程的核心逻辑

合并两个有序数组（如升序的 $ A $ 和 $ B $）时，通常采用“双指针法”：

指针 $ i $ 指向 $ A $ 的当前元素，指针 $ j $ 指向 $ B $ 的当前元素；
每次比较 $ A[i] $ 和 $ B[j] $，将较小的元素放入结果数组，并移动对应指针；
当其中一个数组的所有元素都被处理完后，剩余数组的元素可直接按顺序放入结果，无需额外比较。

最坏情况的推导

最坏情况发生在两个数组的元素“交替需要比较”的场景（如 $ A = [1, 3, 5, \dots, 2n-1] $，$ B = [2, 4, 6, \dots, 2n] $）。此时：

合并后的数组长度为 $ 2n $；
前 $ 2n-1 $ 个元素的位置，每次都需要比较 $ A $ 和 $ B $ 的当前元素（因为每次比较后，只有一个元素被放入结果，另一个数组的元素仍需继续参与比较）；
第 $ 2n $ 个元素（最后一个元素）必然来自其中一个数组，此时该数组的前 $ n-1 $ 个元素已全部处理完毕，因此无需比较，可直接放入。

举例验证（以 $ n=2 $ 为例）

设 $ A = [1, 3] $，$ B = [2, 4] $，合并过程：

比较 $ 1 $ 和 $ 2 $ → 放 $ 1 $（比较次数 $ 1 $）；
比较 $ 3 $ 和 $ 2 $ → 放 $ 2 $（比较次数 $ 2 $）；
比较 $ 3 $ 和 $ 4 $ → 放 $ 3 $（比较次数 $ 3 $）；
直接放 $ 4 $（无需比较）。

总比较次数为 $ 3 = 2 \times 2 - 1 $，符合 $ 2n - 1 $ 的规律。

综上，两个长度为 $ n $ 的有序数组合并，最坏情况下至少需要 $ 2n - 1 $ 次比较，对应选项 D。

noip2017

小明要去南美洲旅游，一共乘坐三趟航班才能到达目的地，其中第
1 个航班准点的概率是
0.9，第 2 个航班准点的概率为 0.8，第 3 个航班准点的概率为
0.9。如果存在第 i 个（i=1,2）航班晚点，第 i+1 个航班准点，则小明将赶不上第 i+1 个航班，旅行失败；除了这种情况，其他情况下旅行都能成功。请问小明此次旅行成功的概率是（）。

A. 0.5
B. 0.648
C. 0.72
D. 0.74

题目解释：小明旅行成功的概率计算

要计算旅行成功的概率，需先分析旅行失败的情况，再通过“总概率为1”减去失败概率，得到成功概率。

步骤1：定义事件与概率

设：

$ A_1 $：第1班航班准点，$ P(A_1) = 0.9 $，因此 $ P(\overline{A_1}) = 1 - 0.9 = 0.1 $（$ \overline{A_1} $ 表示第1班晚点）；
$ A_2 $：第2班航班准点，$ P(A_2) = 0.8 $，因此 $ P(\overline{A_2}) = 1 - 0.8 = 0.2 $（$ \overline{A_2} $ 表示第2班晚点）；
$ A_3 $：第3班航班准点，$ P(A_3) = 0.9 $，因此 $ P(\overline{A_3}) = 1 - 0.9 = 0.1 $（$ \overline{A_3} $ 表示第3班晚点）。

步骤2：分析失败情况

题目规定：若存在第 $ i $ 班（$ i=1,2 $）晚点，且第 $ i+1 $ 班准点，则旅行失败。因此失败情况有两种（且两种情况互斥，无重叠）：

第1班晚点，且第2班准点：事件 $ \overline{A_1}A_2 $；
第2班晚点，且第3班准点：事件 $ \overline{A_2}A_3 $。

步骤3：计算失败概率

根据“独立事件概率乘法公式”（航班是否准点相互独立）：

情况1的概率：$ P(\overline{A_1}A_2) = P(\overline{A_1}) \times P(A_2) = 0.1 \times 0.8 = 0.08 $；
情况2的概率：$ P(\overline{A_2}A_3) = P(\overline{A_2}) \times P(A_3) = 0.2 \times 0.9 = 0.18 $；

由于两种失败情况互斥，总失败概率为：
$ P(\text{失败}) = P(\overline{A_1}A_2) + P(\overline{A_2}A_3) = 0.08 + 0.18 = 0.26 $

步骤4：计算成功概率

因为“成功”与“失败”是对立事件（总概率为1），因此成功概率为：
$ P(\text{成功}) = 1 - P(\text{失败}) = 1 - 0.26 = 0.74 $

综上，小明此次旅行成功的概率是 $ 0.74 $，对应选项 D。

12套t9

若 n,m 都是 0~255 中的整数则有（）对 n+m=(n and m) xor (n or m)
a. 256
b. 6561
c. 6739
d. 65536

问题分析：寻找满足 $ n + m = (n \text{ and } m) \text{ xor } (n \text{ or } m) $ 的数对

要解决这个问题，需从位运算的按位性质入手，推导等式成立的条件，并计算合法数对的数量。

步骤1：按位分析等式的局部成立性

对于二进制的每一位（设 $ n $ 和 $ m $ 的某一位为 $ a, b \in {0,1} $），逐一验证四种组合：

$ a $	$ b $	$ n+m $ 该位贡献	$ (a \text{ and } b) \text{ xor } (a \text{ or } b) $	等式是否成立？
0	0	0	$ 0 \text{ xor } 0 = 0 $	是
0	1	1	$ 0 \text{ xor } 1 = 1 $	是
1	0	1	$ 0 \text{ xor } 1 = 1 $	是
1	1	0（但产生进位）	$ 1 \text{ xor } 1 = 0 $	否（进位破坏高位等式）

步骤2：推导等式成立的充要条件

当且仅当 $ n $ 和 $ m $ 的每一位都不同时为1（即 $ n \text{ and } m = 0 $）时，加法无进位，此时 $ n + m = n \text{ xor } m $。

同时，若 $ n \text{ and } m = 0 $，则 $ (n \text{ and } m) \text{ xor } (n \text{ or } m) = 0 \text{ xor } (n \text{ xor } m) = n \text{ xor } m $，与 $ n + m $ 相等。

步骤3：计算合法数对的数量

对于8位二进制数（0~255），每一位有3种合法组合（$ (0,0)、(0,1)、(1,0) $），且8位相互独立。因此总组合数为： $
3^8 = 6561
$

最终，满足条件的数对数量为 $ 6561 $，答案为 b。

12套t14

在1~10的所有排列中，有（）个满足3排在第2为，且与1相邻的数都是偶数。
a.86400
b.100800
c.111600
d.120960

步骤 1：固定 3 的位置

第 2 位（索引为 1）必须是 3，仅 1 种选择。

步骤 2：分析 1 的合法位置（需相邻数为偶数）

1~10 中偶数为 ${2,4,6,8,10}$（共 5 个），奇数为 ${1,3,5,7,9}$
（3 已固定在第 2 位）。

“与 1 相邻的数都是偶数” 要求：

1不能在第 1 位：右侧（第 2 位）是 3（奇数），不满足。

1不能在第 3 位：左侧（第 2 位）是 3（奇数），不满足。

因此，1 的合法位置为 第 4~9 位（共 6 个位置）和 第 10 位（最后一位）。

步骤 3：分情况计算排列数

情况 1：1 在第 10 位（最后一位）

此时 1 只有 左侧（第 9 位） 相邻，需为偶数。

从 5 个偶数中选 1 个放第 9 位：
$\binom{5}{1}=5$ 种选择。

剩余 7 个数字（10 个数字用了 3、1、1 个偶数）全排列：
7!=5040
种.

情况 1 总排列数：
$5×5040=25200$
。

情况 2：1 在第 4~9 位（共 6 个位置）

此时 1 有左侧和右侧两个相邻位置，都需为偶数。

从 5 个偶数中选 2 个排列在左右两侧（位置不同，是排列）：
$A_5^2=5×4=20$
种选择。

剩余 6 个数字（10 个数字用了 3、1、2 个偶数）全排列：
6!=720
种。

情况 2 总排列数：
$6×20×720=86400$
。

步骤 4：总排列数

将两种情况相加：
25200+86400= 111600。

sshwy题无法过编。。

c++中使用char *a[2](); 声明的变量a的含义是
a.一个指向长度为2的由char构成的数组的指针
b.一个指向长度为2的由返回char的函数构成的数组的指针
c.一个长度为2的由返回char *的函数构成的数组
d.一个返回值为长度为2的由char *构成的数组的函数指针

要解析这道 C++ 声明题，核心是掌握 C++ 声明语法的 “运算符优先级规则” 和 “从变量出发拆解类型” 的方法。我们一步步拆解声明、匹配选项，就能清晰得出结论。

一、先明确核心规则：C++ 声明的 “运算符优先级”

C++ 中，声明的解析需遵循 “先绑定优先级高的运算符” 原则，关键优先级顺序为：
()（函数调用）、[]（数组下标） > *（指针）

简单说：声明中，变量会先和()或[]结合，再和*结合。这是拆解所有复杂声明的基础。

二、拆解原声明：`char *a[2]()`;

我们以变量a为核心，按优先级逐步拆解：

第一步：确定a的基础类型（数组 / 函数 / 指针）

a后面直接跟着[2]（数组下标），且[]优先级高于*，因此 a首先是一个 “长度为 2 的数组”（不是指针、也不是函数）。

第二步：确定数组的 “元素类型”

数组a[2]后面还有()（函数调用符号），因此数组的每个元素是 “函数”（不是普通变量或指针）。

第三步：确定函数的 “返回类型”

声明最前面的 char * 是函数的返回值类型，因此数组中的每个函数，**返回类型是char ***（指向字符的指针）。

综上，原声明的语法含义是：

a是长度为 2 的数组，数组的每个元素是返回char*类型的无参函数。

三、逐一分析选项（对比拆解结果）

A 一个指向长度为 2 的由 char 构成的数组的指针

拆解结果中a是数组，不是 “指针”；
声明涉及 “函数”，与 “char 数组” 无关。完全不符。

B 一个指向长度为 2 的由返回 char 的函数构成的数组的指针

a是数组，不是 “指向数组的指针”（无外层*）；
函数返回类型是char*，不是char。双重错误。

C 一个长度为 2 的由返回 char * 的函数构成的数组

与我们的拆解结果完全一致：a是长度 2 的数组，元素是返回char*的函数。正确。

D 一个返回值为长度为 2 的由 char * 构成的数组的函数指针

a是数组，不是 “函数指针”；
声明中无 “返回数组的函数” 结构（C++ 也不允许函数直接返回数组）。完全不符。

总结解题步骤

抓核心变量：找到声明中的变量（本题是a）；
按优先级绑定运算符：先结合()/[]，再结合*，确定变量的基础类型（数组 / 函数 / 指针）；
补全细节：确定数组元素类型、函数返回类型等；
匹配选项：逐一排除与拆解结果不符的选项。

通过这套方法，所有 C++ 复杂声明题（如指针数组、数组指针、函数指针等）都能轻松解析。

sshwy题2

正确的是：
A. 考虑 int x 对于任意初值，表达式 (x==0)||(x!=-x) 始终为 true
B. 考虑 unsigned int x,y 可以使用 (x+y)>>1 始终为 $\lfloor \frac{x+y}{2} \rfloor$
C. 考虑 int x 对于任意初值，表达式 ((x>>1)<<1)<=x 始终为 true
D. 考虑 int x,y,z 则 (int)((double)x+(double)y+(double)z) 不一定等于 x+y+z，因为浮点数运算可能会丢失精度。

要解决这道题，需逐一分析每个选项，结合有符号整数（int）的补码特性、算术右移规则、无符号整数（unsigned int）的溢出特性及浮点数（double）的精度范围展开判断：

选项 A

分析：(x==0)||(x!=-x) 并非始终为 true

核心问题：有符号整数的最小负值无法表示其相反数。

int 是有符号类型，通常用补码表示（如 32 位 int 范围：$-2^{31} ~ 2^{31}-1$）。其中最小负值为$-2^{31}$（即-2147483648），其特点是：

计算 -x 时，-(-2147483648) = 2147483648，超出 32 位 int 的最大值2147483647，导致溢出。
根据补码规则，溢出后-x的结果仍为-2147483648（即x == -x）。

此时：

x==0为false（x 是最小负值），x!=-x为false（x 等于 - x），整个表达式为false。

因此，A 错误。

选项 B

分析：(x+y)>>1 并非始终为⌊(x+y)/2⌋

核心问题：无符号整数的溢出会导致结果偏差。

unsigned int 是无符号类型，运算溢出时按 “模$2^n$”（n 为位数，如 32 位则模 $2^{32}$）处理。当 x+y 溢出时，(x+y)>>1的结果会与 $\lfloor \frac{x+y}{2} \rfloor$ 不一致。

示例（32 位 unsigned int）：
设x = y = 0xFFFFFFFE（即 $2^{32}-2$ ），则：

实际x+y = (2³²-2)+(2³²-2) = 2³³-4，⌊(x+y)/2⌋ = 2³²-2（即0xFFFFFFFE）。
但 unsigned int 溢出后，x+y的存储值为(2³³-4) mod 2³² = 0xFFFFFFFC，再右移 1 位得0x7FFFFFFE。

显然 0x7FFFFFFE ≠ 0xFFFFFFFE，因此B 错误。

选项 C

分析：((x>>1)<<1) <= x 始终为true

核心规则：有符号 int 的右移是算术右移（符号位扩展），右移后左移等价于 “清掉 x 的最低位”。

无论 x 是正、负、零，清掉最低位后的值始终≤原 x：

正数：如x=5（二进制101），x>>1=2（10），(x>>1)<<1=4（100），4<=5成立。
负数：如x=-5（32 位补码0xFFFFFFFB），x>>1=0xFFFFFFFD（-3，算术右移符号位扩展），(x>>1)<<1=0xFFFFFFFA（-6），-6 <= -5成立。
零：x=0，(0>>1)<<1=0，0<=0成立。

所有情况下表达式均为true，因此C 正确。

选项 D

分析：(int)((double)x+(double)y+(double)z) 与x+y+z始终相等

强制转换为 int 时，若和在 int 范围内，结果与x+y+z完全一致

因此，浮点数运算在此处不会丢失精度，两者始终相等，D 错误。

最终答案：C

sshwy题3

关键背景知识

快速排序核心流程：选择 pivot → 分区（≤pivot 放左，≥pivot 放右）→ 递归处理子数组。
稳定性定义：排序后，相等元素的相对位置是否保持不变（快排的不稳定性源于分区时的交换逻辑，可能打乱相等元素位置）。
时间复杂度影响因素：pivot 选择决定分区平衡性 —— 平衡分区（子数组大小接近）则复杂度低，极端分区（子数组大小 1 和 n-1）则复杂度高。

选项分析

先回忆快速排序的核心逻辑

快速排序的 “快”，关键在于选一个 pivot（基准值），然后把数组分成两部分：左边≤pivot，右边≥pivot，再递归处理两边。整个算法的性能（速度、稳定性）很大程度上和 “怎么选 pivot” 以及 “怎么分区” 有关。

选项 A：“随机选 pivot 的快排，不稳定性和 pivot 选择关系不大，且能改稳定”

结论：正确

什么是 “稳定性”？
简单说：如果原数组中有两个相等的元素（比如 [3, 2, 3]），排序后它们的相对位置和原来一样（还是第一个 3 在第二个 3 前面），就是 “稳定的”；如果位置换了，就是 “不稳定的”。

快排为什么默认不稳定？
问题不在 “选哪个 pivot”，而在 “分区时的交换操作”。比如原数组 [2, 3, 3]，选第一个 3 当 pivot，分区时可能把第二个 3 和 2 交换，变成 [2, 3, 3]（看似稳定），但如果数组是 [3, 2, 3]，选第一个 3 当 pivot，可能会把第二个 3 换到前面，变成 [2, 3, 3]，原来的两个 3 位置反了 —— 这就是不稳定，和 “随机选 pivot” 没关系，换任何 pivot 都可能这样。

能改成稳定的吗？
能！不用改 “随机选 pivot” 的规则，只要改分区方式：比如用一个临时数组，把 “小于 pivot” 的放左边（保持原顺序），“等于 pivot” 的放中间（保持原顺序），“大于 pivot” 的放右边。这样相等元素的相对位置就不会乱，快排就稳定了。

选项 B：“随机选 pivot 的快排，平均 O (nlogn)，最坏 O (n²)”

结论：正确

平均情况 O (nlogn)：
随机选 pivot 时，大概率会选到一个 “中间大小” 的数，把数组分成差不多大的两部分（比如左边 n/2，右边 n/2）。这样递归下去，每层需要处理 n 个元素（总共有 n 个元素），而层数大概是 logn（比如 n=8，分 3 层：8→4→2→1）。总工作量就是 n×logn，即 O (nlogn)。
最坏情况 O (n²)：
虽然概率极低，但理论上可能每次都 “倒霉”—— 随机选到当前数组里最小（或最大）的元素当 pivot。比如数组 [1,2,3,4,5]，每次随机选到 1 当 pivot，分区后左边只有 1，右边有 4 个元素；下次又选到 2，右边剩 3 个…… 最后需要分 n 次（5 次），每次处理 n, n-1, ..., 1 个元素，总工作量是 n+(n-1)+...+1 = n (n+1)/2，差不多是 n²，即 O (n²)。

选项 C：“用确定性 pivot 选择的快排，最坏复杂度一定是 O (n²)”

结论：错误

“确定性 pivot 选择” 指的是 “不随机，按固定规则选 pivot”（比如永远选第一个元素、中间元素，或者用某种公式计算）。

大部分确定性方法确实有 O (n²) 的最坏情况：
比如 “永远选第一个元素” 当 pivot，如果输入数组是有序的（如 [1,2,3,4,5]），每次 pivot 都是最小的，分区后右边越来越大，最终复杂度 O (n²)。
但存在特殊的确定性方法，能避免 O (n²) 的最坏情况：
最典型的是 “BFPRT 算法”（一种专门找 “中位数的中位数” 当 pivot 的方法）。它通过确定性规则选 pivot，能保证每次分区后，子数组的大小至少是原数组的 1/5（不会出现一边特别大、一边特别小的情况）。这样递归层数最多是 logn，总复杂度始终是 O (nlogn)，哪怕最坏情况也一样。

所以 “确定性 pivot 选择的快排，最坏一定是 O (n²)” 是错的 —— 因为有例外（比如 BFPRT）。

选项 D：“就算序列随机打乱，pivot 选得不好，平均复杂度也可能变成 O (n²)”

结论：正确

“随机打乱序列” 本来是为了避免 “有序数组导致 pivot 选到极端值”，但如果 pivot 选择方法本身就有问题，再打乱也没用。

比如：不管序列怎么乱，我偏要 “每次选当前数组里的最小元素” 当 pivot（这是一种 “不恰当的确定性方法”）。即使序列是随机的，每次选到的 pivot 都是最小的，分区后右边还是差不多大（n-1 个元素），递归下去还是需要 n 层，总工作量 n²，平均复杂度自然就成了 O (n²)。

posted @ 2025-09-05 13:59 Slayer-WT!!!!!!!! 阅读(70) 评论(0) 收藏举报

刷新页面返回顶部

VAMOS LOS PIBES

那些杀不死我的只会让我更强大

【初赛】错题

csp2023第6题

解析

核心概念：二分图与2-着色

选项分析

选项A：完全三叉树

选项B：平面图

选项C：边双连通图

选项D：欧拉图

csp2023第10题

解析

本题场景分析

选项分析

csp2023第12题

解析

选项分析

选项A：4个结点的树

选项B：6个结点的树

选项C：7个结点的树

选项D：8个结点的树

csp2023第14题

解析

关键逻辑：不动点与十六进制各位和的关系

范围转换：十六进制转十进制

分析十六进制数的结构

列条件：各位和为 9

csp2023第15题

解析

csp2024第9题

解析

csp2024第10题

解析

csp2024第12题

解析

csp2024第15题

解析

杂题 1

杂题 2

杂题 3

杂题 4

csp2021第5题

解析

csp2021第七题

解析

csp2021第9题

解析

选项A

选项B

选项C

选项D

答案： $\boxed{D} $

csp2021第14题

解析

一、等边三角形（ $a = b = c $）

二、非等边的等腰三角形（有且只有两边相等）

子情况： $a = b = k $（ $k \in [1,9] $）， $c = m $（ $m \in [1,9] $， $m \neq k $）

三、总计

杂题5：

解析：

noip2018s

步骤 1：迭代展开递推式

步骤 2：代入初始条件并求和

步骤 3：分析增长量级

noip2018 t10

选项分析

noip t9

题目解释：抽奖机中红球与蓝球的比例

步骤1：分析单个抽奖者的抽奖过程

步骤2：建立蓝球期望的方程

步骤3：解方程求蓝球期望

步骤4：推广到足够多的人

noip2017

题目解释：两个有序数组合并的最坏比较次数

合并过程的核心逻辑

最坏情况的推导

举例验证（以 $ n=2 $ 为例）

noip2017

题目解释：小明旅行成功的概率计算

sshwy题无法过编。。

二、拆解原声明：`char *a[2]()`;